|
LUNDA
ANIMALS |
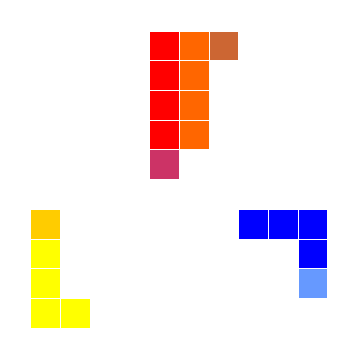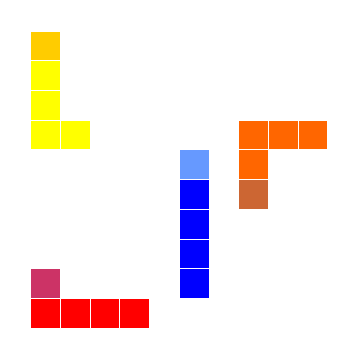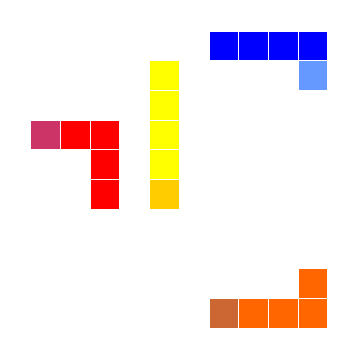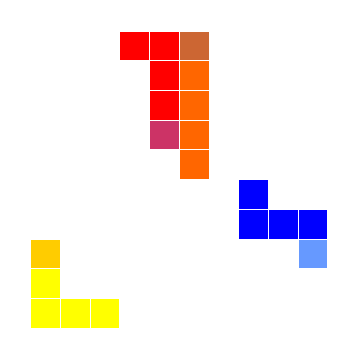 |
|
LUNDA
ANIMALS |
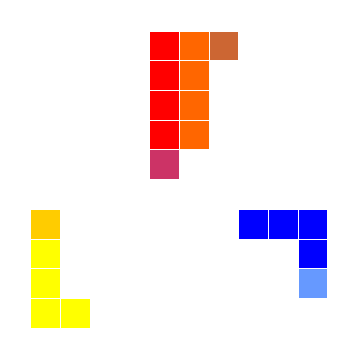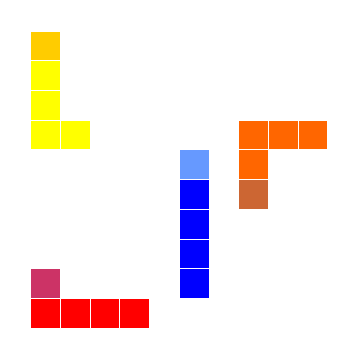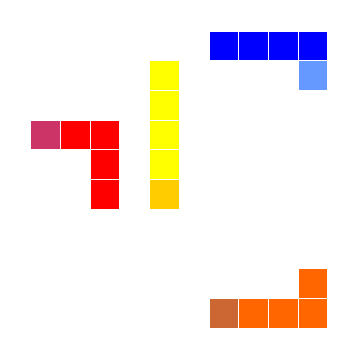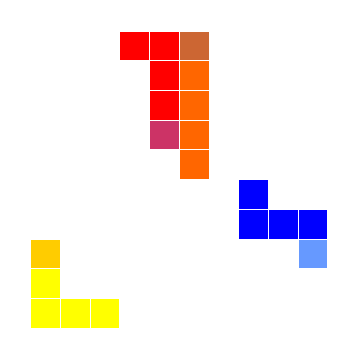 |
|
Lunda-animal is a Lunda 5-omino with one unit square at one of its ends representing a head. A Lunda-animal walks in such a way that after each step the head occupies a new unit square, and each other cell occupies the preceeding one. In other words, two subsequent positions of a Lunda-animal have a Lunda-tetromino in common.
How many different positions p5(n)
of a Lunda 5-omino are possible after n steps?
for n=1,2,3,..., where f (n) is the famous Fibonacci sequence 0,1,1,2,3,5,8,13,21,34... given by the recurrence formula: f (n+1) = f (n) + f (n-1).
It is interesting that for every
Lunda m-omino for m<9 the result is the same, so pm
= f (n+3) for 4<m<9. From m=9 onwards,
pm < f (n+3). Try to find the general
formula for pm!
|