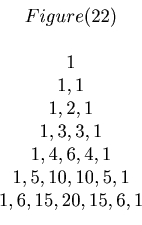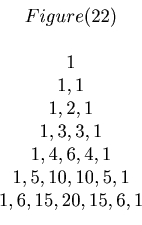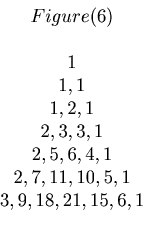


: Overview of the research
: pascal like triangles
: A gallery of beautiful
Contents
It is well known that you can produce the Fibonacci sequence from the Pascal's triangle.
Example 6:
Figure 22 is the well known Pascal's triangle. From this we can produce the Fibonacci sequence by adding numbers.
1, 1, 1+1=2, 1+2 = 3, 1+3+1=5, 1+4+3=8, 1+5+6+1=13, ...
The students tried the same kind of calculation for the Pascal like triangles they made, and found a very interesting fact.
Example 7:
We are going to use Figure 6 again. By using the same method we used in Example 6 we can make a sequence as the followings.
1, 1, 1+1=2, 2+2=4, 2+3+1=6, 2+5+3=10, 3+7+6+1=17,...
The sequence we produced is very much like the Fibonacci sequence. The only difference is to add 1 periodically.
We can also produce Fibonacci like sequence by using other triangles made from
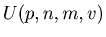 .
.
The authors are now studying these Fibonacci sequence. They could make an interesting formula for these sequences. See [9].
The fact that we can produce Fibonacci like sequences are very important, because this fact shows that these triangles are really Pascal like!



: Overview of the research
: pascal like triangles
: A gallery of beautiful
Contents