Example 1. If we expand ![]() , then we get the following matrix made of numbers. It is easy to see that there are a lot more 0 and 9 than other numbers.
, then we get the following matrix made of numbers. It is easy to see that there are a lot more 0 and 9 than other numbers.
![\includegraphics[height=6cm,clip]{graph9-1.eps}](img7.gif)
We studied numbers that can be expressed as ![]() with
with ![]() , and found out a very interesting fact. We are going to explain the fact by examples.
, and found out a very interesting fact. We are going to explain the fact by examples.
Example 2. When we expand numbers that can be expressed as ![]() with
with ![]() , we have more of 0 and 9 if we make x bigger and make y smaller while we keep the size of the number almost same. We found out this fact by computer experiment, but at first we did not why. For example there is not much difference of size between p =
, we have more of 0 and 9 if we make x bigger and make y smaller while we keep the size of the number almost same. We found out this fact by computer experiment, but at first we did not why. For example there is not much difference of size between p = ![]() and q =
and q = ![]() , but we have much more 0 and 9 in the expansion of q. Please compare the expansions of the numbers p and q by Example 1 and the following calculation.
, but we have much more 0 and 9 in the expansion of q. Please compare the expansions of the numbers p and q by Example 1 and the following calculation.
If we expand q, then we get
![\includegraphics[height=6cm,clip]{graph9-3.eps}](img11.gif)
,and the distribution of digits of q is
Please compare the distributions of the digits of numbers p and q.
Question 2. By Example 2 we know by experiment that we have more of 0 and 9 in the expansion if we make x bigger and make y smaller while we keep the size of these numbers almost the same. But why this kind of thing happens?
Example 3. In Example 2 we compared two numbers. The method was to count the digits in the expansions of p and q. Here we used another way to compare numbers. We substitute numbers 0,1,2,3,4,5,6,7,8,9 with colours. We knew that many mathematicians use colours to show randomness of the numerical series.
We gave similar colours to 0 and 9, because we want to emphasize the fact that there are a lot of 0 and 9 in the expansion.
![\includegraphics[height=1.5cm,clip]{graph9-5.eps}](img13.gif)
Then we can express the number p as the following matrix of colours.
![\includegraphics[height=4cm,clip]{graph9-6.eps}](img14.gif)
We also can express the number q as the following matrix of colours.
![\includegraphics[height=4cm,clip]{graph9-7.eps}](img15.gif)
It is easy to see that there are more of 0 and 9 in the expansion of q by its colours.
One student proposed a very good idea. Instead of studying numbers ![]() with
with ![]() he proposed to study numbers with a form
he proposed to study numbers with a form ![]() .
.
After that we began to use ![]() instead of
instead of ![]() .
.
Example 4. In this example we use numbers ![]() with an integer x =
with an integer x = ![]() , and make n bigger and y smaller while we keep the size of these numbers almost the same as that of
, and make n bigger and y smaller while we keep the size of these numbers almost the same as that of ![]() . What we have to do is to choose y such that for each n
. What we have to do is to choose y such that for each n
| (1) | |
By (1) we have
| |
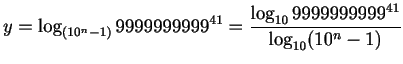 |
|
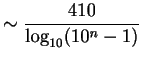 |
(2) |
|
, where we mean by "
| |
![\includegraphics[height=4cm,clip]{graph9-8.eps}](img28.gif)
![\includegraphics[height=4cm,clip]{graph9-9.eps}](img29.gif)
![\includegraphics[height=4cm,clip]{graph9-10.eps}](img30.gif)
![\includegraphics[height=4cm,clip]{graph9-11.eps}](img31.gif)
![\includegraphics[height=3.7cm,clip]{graph9-12.eps}](img32.gif)
Please look at the last one of the above five figures. This is a picture made by expressing the number ![]() for n =30 and y = 13 by colours. We found this figure by chance, but it took us a lot of time to find the mathematical structure of this figure. You can see a sector, and its background consists of the following two colours. These are colours we gave to the numbers 0 and 9. See Figure (1) of Example 3.
for n =30 and y = 13 by colours. We found this figure by chance, but it took us a lot of time to find the mathematical structure of this figure. You can see a sector, and its background consists of the following two colours. These are colours we gave to the numbers 0 and 9. See Figure (1) of Example 3.
Another one is the symmetry in terms of the relation x and y = 9-x between numbers. First we have to omit 13-th row. We are going to compare the first row and the 12-th row. The first row is 999999999999999999999999999987, and the 12-th row is 000000000000000000000000000012. If we are to substitute x with (9-x), then we substitute 9, 8, 7 with 0, 1, 2 respectively. Therefore we can make the 12-th row from the first row. The same thing can be said about other rows.
![\includegraphics[height=6cm,clip]{graph9-15.eps}](img37.gif)
Question 3. Why we have this kind of beautiful sector here? If we express it as a matrix of colours, then we have a beautiful picture. If we express it as a matrix of numbers, then we also have two beautiful symmetries of numbers here. Why we have two kinds of symmetries?