

: The Digits Cube Sum
: Curious Properties of Reiterated
: Curious Properties of Reiterated
One of the most well known reiterated process is the Collatz Problem. See [8].
We are going to define Collatz function 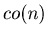 for an arbitrary positive integer.
for an arbitrary positive integer.
Definition 1.1.
We define Collatz fucntion by
Example 1.1.
By using the Mathematica function in Example 10.1 we can study this problem.
For example, if we apply Collatz function co(n) to the number 156 repeatedly by using Mathematica programs in Example 10.1 and 10.2, then we have
{156, 78, 39, 118, 59, 178, 89, 268, 134, 67, 202, 101, 304, 152, 76, 38, 19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1}.
By Mathematica we can make a graph of the above sequence.
Collatz Problem is to prove that the sequence ,m.gif) eventually returns to 1 for any natural number n. This problem is a well
known unsolved problem.
eventually returns to 1 for any natural number n. This problem is a well
known unsolved problem.
Example 1.2.
Even a relatively small number can have a long steps before arriving at 1.
For example the number 27 needs 111 times to arrive at 1. See Graph 1.2.
According to [8] Collatz Problem has been tested and found to always reach 1 for all numbers
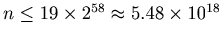 .
.
Example 1.3.
According to
 the number less than 100 million with the longest total stopping time is 63728127 with 949 steps, and
the number less than 1 billion with the longest total stopping time is 670617279 with 986 steps. By using the Mathematica function in Example 10.1 and Example 10.2 we can make the graphs of the sequences that start with 63728127 and 670617279 respectively. See Graph 1.3 and 1.4. The similarity between these graphs is remarkable.
the number less than 100 million with the longest total stopping time is 63728127 with 949 steps, and
the number less than 1 billion with the longest total stopping time is 670617279 with 986 steps. By using the Mathematica function in Example 10.1 and Example 10.2 we can make the graphs of the sequences that start with 63728127 and 670617279 respectively. See Graph 1.3 and 1.4. The similarity between these graphs is remarkable.


: The Digits Cube Sum
: Curious Properties of Reiterated
: Curious Properties of Reiterated
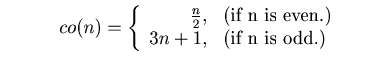
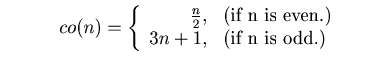
![]() .
.