

: Beautiful graphs produced by
: Combinatorial Games and Beautiful
: Another chocolate problem that
The chocolate problem of Example 2.1 is very difficult to study mathematically, and hence the authors have made a easier version the chocolate problem. This chocolate has a very simple formula to calculate P-positions.
Example 3.1.
Suppose that you have the chocolate in Graph 3.1.
In Graph 3.1 you can cut the chocolate in 3 ways, so it is appropriate to represent it with 3 non-negative integers
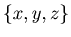 . We represent the position in Graph 3.1 with
. We represent the position in Graph 3.1 with
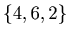 .
It is clear that we have an inequality between these 3 coordinates.
.
It is clear that we have an inequality between these 3 coordinates.
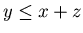 .
.
Note that a list of non-negative numbers
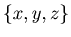 is a position of this chocolate problem when
is a position of this chocolate problem when
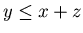 .
.
Theorem 3.1.
The chocolate problem of Example 3.1 has the following simple formula to calculate P-positions.
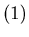 The position {x, 0, z} is a P-position if and only if
The position {x, 0, z} is a P-position if and only if 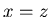 .
.
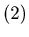 The position {x+1, y, z+1} is a P-position if and only if
The position {x+1, y, z+1} is a P-position if and only if 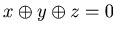 .
.
We are going to prove Theorem 3.1, and we need some corollaries and lemmas.
Remark 3.1.
For convenience's sake we are going to call the chocolate problem of Example 3.2 and the chocolate problem of Example 3.1 the Game 1 and the Game 2 respectively.
Let 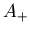 = {
= {
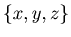 ,
,
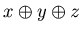 =0 and
=0 and 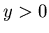 } and
} and 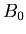 = {
= {
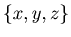 ,
,
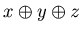 =0 and
=0 and 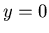 } = {
} = {
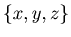 ,
, 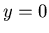 and
and 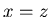 }. Let
}. Let  = {
= {
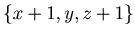 ,
,
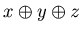 =0 and
=0 and 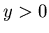 }.
}.
Corollary 3.1.
The list {{x, y, z}, 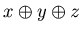 =0} is the set of P-positions of Game 1 and the list {{x, y, z},
=0} is the set of P-positions of Game 1 and the list {{x, y, z}, 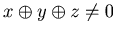 } is the set of N-positions of Game 1.
} is the set of N-positions of Game 1.
Proof.
This is direct from Theorem 1.1.
By Remark 3.1 Game 1 is a special case of the game of Example 1.1, and hence we can use Theorem 1.1 to Game 1 by making the fourth coordinate 0.
Corollary 3.2.
![$ [1] $](img63.gif) If x
If x 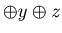 =0, u
=0, u 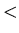 x, v
x, v 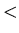 y and w
y and w 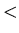 z, then we have
u
z, then we have
u 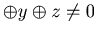 ,
, 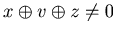 and
and 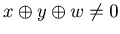 .
.
![$ [2] $](img69.gif) If
If 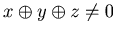 , then at least one of the following three conditions is satisfied.
, then at least one of the following three conditions is satisfied.
![$ [2.1]$](img70.gif) There exists u such that u
There exists u such that u 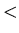 x and
x and 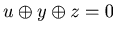 .
.
![$ [2.2]$](img72.gif) There exists v such that v
There exists v such that v 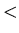 y and
y and 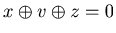 .
.
![$ [2.3]$](img74.gif) There exists w such that w
There exists w such that w 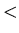 z and
z and 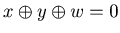 .
.
Proof. [1].
This is direct from Corollary 3.1 and the definition of P-positions and N-Positions. For example if 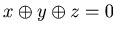 , then by Corollary 3.1 {x, y, z} is a P-position of Game 1. From this position you can move to {u, y, z} with u
, then by Corollary 3.1 {x, y, z} is a P-position of Game 1. From this position you can move to {u, y, z} with u 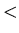 x
x or
{x, v, z} with v 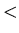 y or {x, y, w} with w
y or {x, y, w} with w 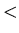 z. Therefore {u, y, z}, {x, v, z} and {x, y, w} are N-positions of Game 2. Therefore we have
z. Therefore {u, y, z}, {x, v, z} and {x, y, w} are N-positions of Game 2. Therefore we have 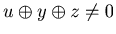 ,
, 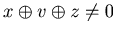 and
and 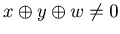 .
.
[2]
If 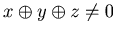 , then by Corollary 3.1 {x, y, z} is an N-position, and hence there should be a option that leads to a N-position.
, then by Corollary 3.1 {x, y, z} is an N-position, and hence there should be a option that leads to a N-position.
Therefore at least one of the conditions ![$ [2.1], [2.2]$](img77.gif) and
and ![$ [2.3]$](img74.gif) are satisfied.
are satisfied.
This is clear from Definition 1.2 and Example 1.2.
Remark 3.2.
By Lemma 3.1 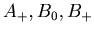
 {{x, y, z},
{{x, y, z}, 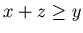 }, and hence if
}, and hence if 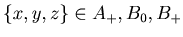 , then
, then 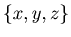 is a position of the chocolate problem of Example 3.1.
is a position of the chocolate problem of Example 3.1.
Lemma 3.2.
For any non-negative integer x {x, 0, x} is an N-position of Game 2, i.e., any element in 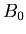 is a P-position of Game 2.
is a P-position of Game 2.
Proof.
For the list {{x, y, z}, with y = 0} , Game 1 and Game 2 have the same mathematical structure. Therefore by the fact that 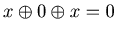 and by Corollary 3.1 we know that {x, 0, x} is an P-position of Game 1, and hence it is an P-position of Game 2.
and by Corollary 3.1 we know that {x, 0, x} is an P-position of Game 1, and hence it is an P-position of Game 2.
Lemma 3.3.
For non-negative integers 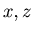 with
with 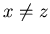 {x,0,z} is an N-position of Game 2.
{x,0,z} is an N-position of Game 2.
Proof. By reducing x or z we can make the first and the third coordinate the same.
Therefore we can move from {x,0,z} to a P-position of Game 2. Therefore {x, 0, z} is an N-position.
Lemma 3.4.
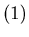 . {0, 0, 0}, {1, 0, 1}, {1, 1, 2}, {2, 0, 2} and {2, 1, 1} are P-positions.
. {0, 0, 0}, {1, 0, 1}, {1, 1, 2}, {2, 0, 2} and {2, 1, 1} are P-positions.
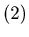 . {0, 0, 1}, {0, 0, 2}, {0, 0, 3}, {0, 0, 4}, {0, 1, 1}, {0, 1, 2}, {0,
1, 3}, {0, 2, 2}, {1, 0, 0}, {1, 0, 2}, {1, 0, 3}, {1, 1, 0}, {1, 1, 1},
{1, 2, 1}, {2, 0, 0}, {2, 0, 1}, {2, 1, 0}, {2, 2, 0}, {3, 0, 0}, {3, 0,
1}, {3, 1, 0} and {4, 0, 0} are N-positions.
. {0, 0, 1}, {0, 0, 2}, {0, 0, 3}, {0, 0, 4}, {0, 1, 1}, {0, 1, 2}, {0,
1, 3}, {0, 2, 2}, {1, 0, 0}, {1, 0, 2}, {1, 0, 3}, {1, 1, 0}, {1, 1, 1},
{1, 2, 1}, {2, 0, 0}, {2, 0, 1}, {2, 1, 0}, {2, 2, 0}, {3, 0, 0}, {3, 0,
1}, {3, 1, 0} and {4, 0, 0} are N-positions.
Proof. By Definition of P-position {0, 0, 0} is a P-position. By Lemma 3.2 {1, 0, 1}, and {2, 0, 2} are P-positions.
It is easy to see that {0, 0, 1}, {0, 0, 2}, {0, 0, 3}, {0, 0, 4}, {0, 1, 1}, {0, 1, 2}, {0, 1, 3}, {0, 2, 2}, {1, 0, 0}, {1, 1, 0}, {2, 0, 0}, {2, 1, 0}, {2, 2, 0}, {3, 0, 0},{3, 1, 0} and {4, 0, 0} are N-positions, since you can move from each of them to {0, 0, 0}. For example, if you have {2, 1, 0}, then by subtracting 2 from the first coordinate you get {0, 0, 0}, since the position should satisfy the inequality 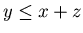 .
.
{1, 0, 2}, {1, 0, 3}, {1, 1, 1}, {1, 2, 1}, {2, 0, 1} and {3, 0, 1} are N-positions, since you can move from each of them to {1, 0, 1} that is a P-position.
From {1, 1, 2} we can move to {0,1,2}, {1,0,2}, {1,1,1} and {1,1,0}, and we have proved that these 4 positions are N-positions. Therefore {1, 1, 2} is a P-position. Similarly {2, 1, 1} is a P-position.
Lemma 3.5.
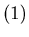 For any non-negative integers
For any non-negative integers 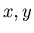 with
with 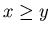 {x, y, 0} is an N-position of Game 2.
{x, y, 0} is an N-position of Game 2.
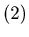 For any non-negative integers
For any non-negative integers 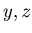 with
with 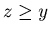 {0, y, z} is an N-position of Game 2.
{0, y, z} is an N-position of Game 2.
Proof.
From {x, y, 0} we can move to {0, 0, 0}, and hence {x, y, 0} is an N-position of Game 2.
Note that you get {0,0,0} by subtracting x and the condition of the inequality. Similarly {0, y, z} is an N-position of Game 2.
We are going to prove the following Theorem 3.2 that is essentially the same as Theorem 3.1.
Theorem 3.2.
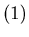 Any element in
Any element in 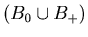 is a P-position of Game 2.
is a P-position of Game 2.
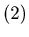 Any element in {{x,y,z} , x + z
Any element in {{x,y,z} , x + z 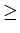 y} -
y} -
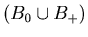 is an N-position of Game 2.
is an N-position of Game 2.
Proof.
We have already proved that any element in 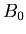 is a P-position of Game 2.
We are going to use Mathematical induction on the size of sum of 3 coordinates.
is a P-position of Game 2.
We are going to use Mathematical induction on the size of sum of 3 coordinates.
![$ [1] $](img63.gif) { {x, y, z}, {x, y, z}
{ {x, y, z}, {x, y, z} 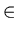
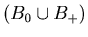 and }
and }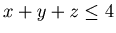
=
{{0, 0, 0}, {1, 0, 1}, {1, 1, 2}, {2, 0, 2}, {2, 1, 1}}.
By Lemma 3.4 any position in {{x, y, z}, {x, y, z} 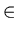
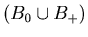 and
and 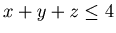 } is a P-position of Game 2.
} is a P-position of Game 2.
{{x,y,z}, 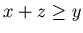 and
and 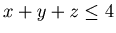 }- {{x, y, z}, {x, y, z}
}- {{x, y, z}, {x, y, z} 
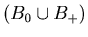 and
and 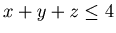 } = {{0, 0, 1}, {0, 0, 2}, {0, 0, 3}, {0, 0, 4}, {0, 1, 1}, {0, 1, 2}, {0, 1, 3}, {0, 2, 2}, {1, 0,
0}, {1, 0, 2}, {1, 0, 3}, {1, 1, 0}, {1, 1, 1}, {1, 2, 1}, {2, 0, 0}, {2,
0, 1}, {2, 1, 0}, {2, 2, 0}, {3, 0, 0}, {3, 0, 1}, {3, 1, 0}, {4, 0, 0}}, and hence by Lemma 3.4 any position in {{x,y,z},
} = {{0, 0, 1}, {0, 0, 2}, {0, 0, 3}, {0, 0, 4}, {0, 1, 1}, {0, 1, 2}, {0, 1, 3}, {0, 2, 2}, {1, 0,
0}, {1, 0, 2}, {1, 0, 3}, {1, 1, 0}, {1, 1, 1}, {1, 2, 1}, {2, 0, 0}, {2,
0, 1}, {2, 1, 0}, {2, 2, 0}, {3, 0, 0}, {3, 0, 1}, {3, 1, 0}, {4, 0, 0}}, and hence by Lemma 3.4 any position in {{x,y,z}, 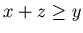 and }
and }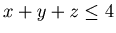 }- {{x, y, z}, {x, y, z}
}- {{x, y, z}, {x, y, z} 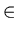
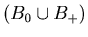 and
and 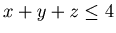 } is an N-position of Game 2. Therefore Theorem 2 is valid for any {x, y, z} such that
} is an N-position of Game 2. Therefore Theorem 2 is valid for any {x, y, z} such that 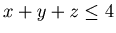 .
.
![$ [2] $](img69.gif) We suppose that the conclusion of this theorem is valid for {x, y, z} with
We suppose that the conclusion of this theorem is valid for {x, y, z} with 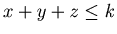 .
.
![$ [2.1]$](img70.gif) We are going to prove
We are going to prove 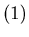 of this theorem for {x, y, z} with
of this theorem for {x, y, z} with 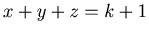 . By Lemma 3.2 we have only to show that {x+1,y,z+1} is a P-position of Game 2 when (x+1) + y +(z+1) = k + 1,
. By Lemma 3.2 we have only to show that {x+1,y,z+1} is a P-position of Game 2 when (x+1) + y +(z+1) = k + 1, 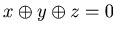 and
and 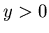 . It is sufficient to prove that any position that can be reached from {x+1,y,z+1} is an N-position of Game 2. Note that we have
. It is sufficient to prove that any position that can be reached from {x+1,y,z+1} is an N-position of Game 2. Note that we have
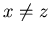 |
(3.1) |
,since 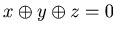 and
and 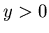 .
.
![$ [2.1.1]$](img95.gif) Suppose that we move from {x+1,y,z+1} to {x+1,0,z+1}. By
Suppose that we move from {x+1,y,z+1} to {x+1,0,z+1}. By 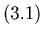 and Lemma 3.3 {x+1,0,z+1} is an N-position of Game 2.
and Lemma 3.3 {x+1,0,z+1} is an N-position of Game 2.
![$ [2.1.2]$](img97.gif) Suppose that we move from {x+1,y,z+1} to {x+1,v,z+1} with v
Suppose that we move from {x+1,y,z+1} to {x+1,v,z+1} with v 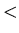 y. Since
y. Since 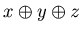 =0, by
=0, by 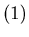 of Corollary 3.2 we have
of Corollary 3.2 we have 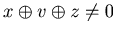 , and hence {x+1,v,z+1
, and hence {x+1,v,z+1}
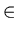 {{x,y,z},
{{x,y,z}, 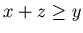 } -
} -
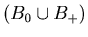 and
and
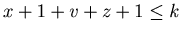 . Therefore by the hypothesis of Mathematical induction {x+1,v,z+1} is an N-position of Game 2.
. Therefore by the hypothesis of Mathematical induction {x+1,v,z+1} is an N-position of Game 2.
![$ [2.1.3.1]$](img99.gif) Suppose that we move from {x+1,y,z+1} to {x+1,y ,w+1} with w
Suppose that we move from {x+1,y,z+1} to {x+1,y ,w+1} with w 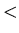 z. Since
z. Since 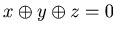 , by
, by 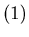 of Corollary 3.2 we have
of Corollary 3.2 we have 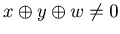 .
By the same argument that we used in
.
By the same argument that we used in ![$ [2.1.2]$](img97.gif) we know that {x+1,y ,w+1} is an N-position of Game 2.
we know that {x+1,y ,w+1} is an N-position of Game 2.
![$ [2.1.3.2]$](img100.gif) Suppose that we move from {x+1,y,z+1
Suppose that we move from {x+1,y,z+1}
to {x+1,y ,0}, then we have 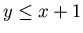 . Therefore by Lemma 3.5 {x+1,y ,0
. Therefore by Lemma 3.5 {x+1,y ,0}
is an N-position of Game 2.
![$ [2.1.4.1]$](img102.gif) Suppose that we move from {x+1,y,z+1} to {x+1,v ,w+1} with v
Suppose that we move from {x+1,y,z+1} to {x+1,v ,w+1} with v 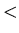 y and w
y and w 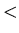 z. This is a case that two coordinates decreased at the same time by the
inequality between 3 coordinates, and hence we have (x+1)+(w+1) = v. Since x + w
z. This is a case that two coordinates decreased at the same time by the
inequality between 3 coordinates, and hence we have (x+1)+(w+1) = v. Since x + w 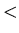 v, by Lemma 3.1
v, by Lemma 3.1 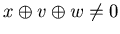 . By the hypothesis of mathematical induction {x+1,v ,w+1} is an N-position of Game 2.
. By the hypothesis of mathematical induction {x+1,v ,w+1} is an N-position of Game 2.
![$ [2.1.4.2]$](img104.gif) Suppose that we move from {x+1,y,z+1} to {x+1,v ,0} with v
Suppose that we move from {x+1,y,z+1} to {x+1,v ,0} with v 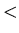 y. Then by Lemma 3.5 {x+1,v ,0} is an N-position of Game 2.
y. Then by Lemma 3.5 {x+1,v ,0} is an N-position of Game 2.
When we subtract a natural number from the first coordinate, we can use the method that we used in ![$ [2.1.3.1], [2.1.3.2], [2.1.4.1], [2.1.4.2]$](img105.gif) .
.
![$ [2.2]$](img72.gif) We are going to prove
We are going to prove 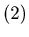 of this theorem for {x, y, z} with
of this theorem for {x, y, z} with 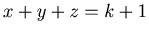 . Let {p, q, r}
. Let {p, q, r}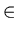
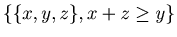 -
- 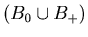 such that p + q + r = k + 1. If
such that p + q + r = k + 1. If 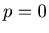 or
or 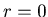 , then by Lemma 3.5 {p, q, r} is an N-position of Game 2.
, then by Lemma 3.5 {p, q, r} is an N-position of Game 2.
Now we can suppose that 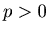 and
and 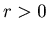 , and there exist non-negative numbers
, and there exist non-negative numbers 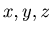 such that
such that 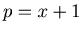 ,
, 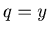 and
and 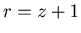 . Therefore we have only to show that {x+1,y,z+1} is an N-position of Game 2 when
. Therefore we have only to show that {x+1,y,z+1} is an N-position of Game 2 when 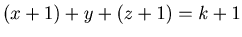 and
and 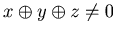 and
and 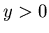 . It is sufficient to prove that there exists a P-position of Game 2 that can be reached from {x+1,y,z+1}
. It is sufficient to prove that there exists a P-position of Game 2 that can be reached from {x+1,y,z+1}.
If 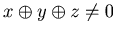 , then by Corollary 3.2 at least one of the following three conditions are satisfied.
, then by Corollary 3.2 at least one of the following three conditions are satisfied.
![$ [2.2.1] $](img115.gif) There exists u such that
There exists u such that 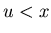 and
and 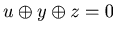 .
By Lemma 3.1
.
By Lemma 3.1 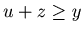 , and hence
, and hence 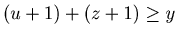 . Therefore by the hypothesis of mathematical induction we have that {u+1, y, z+1} is a P-position of Game 2.
. Therefore by the hypothesis of mathematical induction we have that {u+1, y, z+1} is a P-position of Game 2.
![$ [2.2.2]$](img119.gif) There exists v such that
There exists v such that 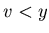 and
and 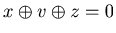 .
.
Similarly {x+1, v, z+1} is a P-position of Game 2.
![$ [2.2.3] $](img121.gif) There exists w such that
There exists w such that 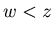 and
and 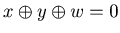 . Similarly {x+1, y, w+1} is a P-position of Game 2.
. Similarly {x+1, y, w+1} is a P-position of Game 2.


: Beautiful graphs produced by
: Combinatorial Games and Beautiful
: Another chocolate problem that

![]() = {
= {
![]() ,
,
![]() =0 and
=0 and ![]() } and
} and ![]() = {
= {
![]() ,
,
![]() =0 and
=0 and ![]() } = {
} = {
![]() ,
, ![]() and
and ![]() }. Let
}. Let ![]() = {
= {
![]() ,
,
![]() =0 and
=0 and ![]() }.
}.![]() .
.
![]()
![]() and
and ![]() } is a P-position of Game 2.
} is a P-position of Game 2. ![]() and
and ![]() }- {{x, y, z}, {x, y, z}
}- {{x, y, z}, {x, y, z} ![]()
![]() and
and ![]() } = {{0, 0, 1}, {0, 0, 2}, {0, 0, 3}, {0, 0, 4}, {0, 1, 1}, {0, 1, 2}, {0, 1, 3}, {0, 2, 2}, {1, 0,
0}, {1, 0, 2}, {1, 0, 3}, {1, 1, 0}, {1, 1, 1}, {1, 2, 1}, {2, 0, 0}, {2,
0, 1}, {2, 1, 0}, {2, 2, 0}, {3, 0, 0}, {3, 0, 1}, {3, 1, 0}, {4, 0, 0}}, and hence by Lemma 3.4 any position in {{x,y,z},
} = {{0, 0, 1}, {0, 0, 2}, {0, 0, 3}, {0, 0, 4}, {0, 1, 1}, {0, 1, 2}, {0, 1, 3}, {0, 2, 2}, {1, 0,
0}, {1, 0, 2}, {1, 0, 3}, {1, 1, 0}, {1, 1, 1}, {1, 2, 1}, {2, 0, 0}, {2,
0, 1}, {2, 1, 0}, {2, 2, 0}, {3, 0, 0}, {3, 0, 1}, {3, 1, 0}, {4, 0, 0}}, and hence by Lemma 3.4 any position in {{x,y,z}, ![]() and }
and }![]() }- {{x, y, z}, {x, y, z}
}- {{x, y, z}, {x, y, z} ![]()
![]() and
and ![]() } is an N-position of Game 2. Therefore Theorem 2 is valid for any {x, y, z} such that
} is an N-position of Game 2. Therefore Theorem 2 is valid for any {x, y, z} such that ![]() .
.
![]() We suppose that the conclusion of this theorem is valid for {x, y, z} with
We suppose that the conclusion of this theorem is valid for {x, y, z} with ![]() .
.
![]() We are going to prove
We are going to prove ![]() of this theorem for {x, y, z} with
of this theorem for {x, y, z} with ![]() . By Lemma 3.2 we have only to show that {x+1,y,z+1} is a P-position of Game 2 when (x+1) + y +(z+1) = k + 1,
. By Lemma 3.2 we have only to show that {x+1,y,z+1} is a P-position of Game 2 when (x+1) + y +(z+1) = k + 1, ![]() and
and ![]() . It is sufficient to prove that any position that can be reached from {x+1,y,z+1} is an N-position of Game 2. Note that we have
. It is sufficient to prove that any position that can be reached from {x+1,y,z+1} is an N-position of Game 2. Note that we have