|
Tessa Morrison School of Fine Arts,
Introduction The labyrinthine symbol has had a universal appeal throughout history and it is one of the most popular symbols throughout history. Since the dawn of civilization the labyrinth symbol has been an integral part of many myths, religions and rituals. The conceptual depiction of this figure can represent a journey with visible or invisible elements of entrapment or enlightenment, and sometimes both. It is instantly recognizable as embodying one or both of these aspects. It can be very diverse in its meaning such as: the entrapment of an enemy, a friend or a lover; used as a prison; a cure for physical or mental illness by entrapping an evil spirit to cure you or a good spirit to protect you. It can be a journey of enlightenment of knowledge, of the soul, of the body, and in some culture’s myths it is used as a test for reincarnation. For thousands of years the labyrinthine figure has meant many different things to many different people. 
Figure 1: Unicursal and multicursal labyrinths Labyrinths can be divided into two main categories. If the path from the outside to the centre has one and only one only path leading to the centre then it is called a unicursal pattern. If there is more than one path to the centre or there are dead ends, then it is a multicursal pattern. In Figure 1.f. is an example of the multicursal pattern and it is the plan of the famous maze hedge at Hampton Court Palace, England. The Hampton Court Palace maze is the oldest surviving Hedge maze in Britain. This maze originated in Elizabethan times but was replanted in 1690 [2]. The multicursal labyrinth is a relatively modern concept, which became a very popular architectural and landscape feature in the renaissance [3]. Most ancient labyrinths are unicursal and this analysis investigates unicursal labyrinths. The unicursal labyrinths can be divided into three main categories; the Roman labyrinth (Figure 1.e), the Church labyrinth (Figure 1.d) and the simple alternative transitive labyrinth or SAT labyrinth (Figure 1.a & b). This examination will expand on these three categorizes. The primary aim of this paper is to examine the topology that is to analyze the properties of the labyrinth. These properties depend only on the relative position of the elements of the labyrinth and are independent of whether the labyrinth is round or square, small or large. In strict mathematical terms the topology of a unicursal labyrinth is a straight line. Since a straight line is not going to convey any information on cultural transference this investigation is using the term topology in a very loose sense and concentrates primarily on the configuration of the turns within the labyrinth. In order to facilitate the investigation of the topology of labyrinths a number of restrictions need to be enforced. R1. There are an equal number of paths or levels of the labyrinth equidistant from the centre, so that the levels are concentric levels. These can be concentric circles, squares or any geometric shape as long as they are parallel and equidistant to the centre. Each level has maximum coverage meaning the only gaps on a level are for turns. R2. The unicursal labyrinths have a restricted anatomy, as describe below. R3.
There are a finite number of levels.
The anatomy of the unicursal labyrinth 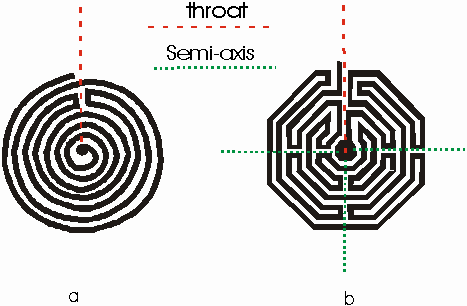
Figure 2: The anatomy of the unicursal labyrinth To examine the structure of the unicursal labyrinth we first need to define the anatomy of unicursal labyrinths. The labyrinth with a unicursal topology has one path, from the outside to the centre, never crossing itself. The paths either spiral, that is covers a number of levels in the same direction before changing direction, or they obey the law of alternation, meaning that the direction of the path changes whenever the level of the labyrinth changes. In Figure 2 there are both of these cases, in 2.a. the labyrinth has both spirals and the law of alternation also it has only one semi-axis. The semi-axes run from the centre to the outside and indicate the position of the turns. Figure 2.b has four semi-axes and only obeys the law of alteration. 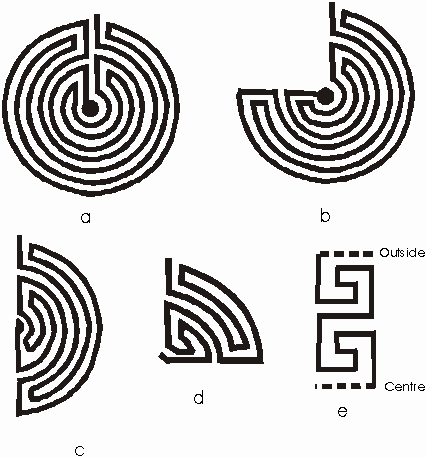
Figure 3: Unrolling the labyrinth The semi-axis from the entrance to the centre is called the throat. The only paths this semi-axis cuts are the paths of a spiral. If there are no spirals and only the law of alternation applies then the throat is clear of paths, such as in Figure 2.b. The other semi-axes marks turns but these semi-axes also cut through levels with a path. If there is only one semi-axis then it must be the throat. In examining the topology of the labyrinth at Chartre Cathedral and similar unicursal structures P. Rosenstiehl [4] developed an algorithm for unrolling the labyrinth. This algorithm begins by dividing the labyrinth at the throat and unrolls it into a rectangular form. Using the so-called ‘Cretan Labyrinth’ Figure 3 shows the method that Rosenstiehl developed. This algorithm divides the labyrinth at the throat and pushes the pattern of the labyrinth to its fundamental form, to highlight its topology. The dotted lines indicate the centre and the outside. Definition:A fundamental form or FF is the rectangular graph obtained when a labyrinth is unrolled. An important aspect of looking at these labyrinths is the level sequence. An American mathematician, Anthony Phillips, has examined the combinatorial problem of how many different n-level labyrinths there are for labyrinths with no spirals and only one semi-axis, the throat, such as the ‘Cretan labyrinth’ [5]. The plan of the labyrinth is a number of parallel or concentric levels, the direction of the path changes whenever the level changes. These labyrinths obey only the law of alternation. These labyrinths Phillips calls simple, alternating, transitive labyrinths or SAT labyrinths. To simplify a topological classification of the SAT labyrinths Phillips looked at the sequence in which the levels are reached by the path of the labyrinth. Since there are no spirals each level will run in the opposite direction to the levels running next to it. So the sequence will run odd and even integers alternatively. For example, the ‘Cretan labyrinth’ is on eight concentric levels, the sequence starts from zero, which indicate the outside, and finishes with eight, the centre. The level sequence of the ‘Cretan labyrinth’ is 032147658. The important aspect of this, to note is that 3214 is an isomorphic or the 'same as' the sequence 7658. Definition: A FF is constructed from fundamental elements or FE, they are the minimal building blocks or elements of the FF. One or more FEs are stacked vertically to create the FFs. An example of a FE is this level sequence 3214 from the ‘Cretan labyrinth’, it is given the label g4 since the second part of the sequence 7658 is isomorphic to g4 it also has this label, therefore the label of the FF of the ‘Cretan labyrinth’ is SAT[g42]. These two FEs are clearly visible in the FF of the ‘Cretan labyrinth’ (Figure 3.e). Notice that the subscript gives the number of levels in this particular FE sequence and the superscript gives the number of these particular FE there are stacked vertically in succession. The level sequence of the FEs completely determines the topology of SAT labyrinths. Phillips combined the unrolling of the labyrinth and level sequence to investigate the FEs of SAT labyrinths and completed a combinatoric study for n-level labyrinth when 1<n<22 and when n = 24, 26, 28, 30, 32 [6]. The level sequences of the FEs are read beginning from the right-hand side and the levels run from the top to the bottom. The notation of the FE’s stacking is also read from the top to the bottom. Figure 4.a. shows how the levels of the graphs are read and in Figure 4.b. with some examples of the nucleus, which will be explain in a moment, their FEs, duals or negatives and level sequences are shown. The duals of the FEs denote the walls of the labyrinth and the FE the paths of the labyrinth (see Figure 5). However what is interesting is that there are only three main EF that are needed to define the topology of the SAT labyrinth [7]. These are; gn which denotes the FE (n-1)…321n, an examples of this are g2 = 12, g4 =3214 and g6 =543216, jn which denotes 1234…(n-3)(n-2)(n-1)n, also hnwhich denotes the FE 0(n-1)2(n-3)4(n-5)6…5(n-4)3(n-2)1n an example of this is h8 = 72543618. An another two are added am and a2 [an] or [an]a2, the brackets indicate nested turns and n is always even, these are needed for the FFs of the Roman and Church labyrinth. With these five classifications of FE it is possible to classify the overall topology of all unicursal labyrinths. There is an alternative procedure to examine the form of SAT. This procedure stems from an ancient game [8] or was possibly used as a mnemonic devise used for rituals. The game or device begins with a pattern of lines and dots. The pattern of the walls of the labyrinth are drawn by joining up the ends of the figure by arcs, starting with the central pair then the next two ends, the dots are left as dead ends, the game ends with the completed walls of the labyrinth, see Figure 5. So the original pattern forms the nucleus of the SAT and each nucleus is unique to a particular topology. However, the nuclei are more difficult to analyze and a slight change in the order of the level sequence of the labyrinth can give you a radically different nucleus, so they are not satisfactory for measuring changes in the structure of the labyrinth. The beauty of the FE system is that it makes measuring changes easily visible, no matter how slight the changes are. 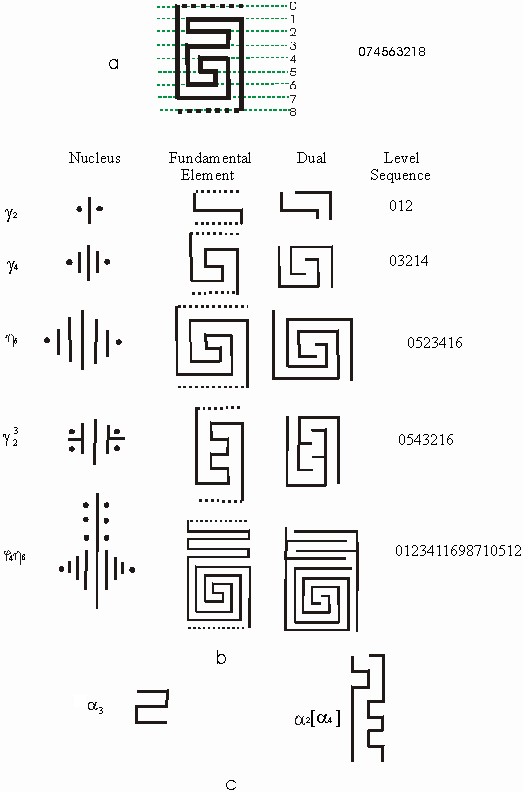
Figure 4: Examples of the Nuclei, Fundamental elements and Duals 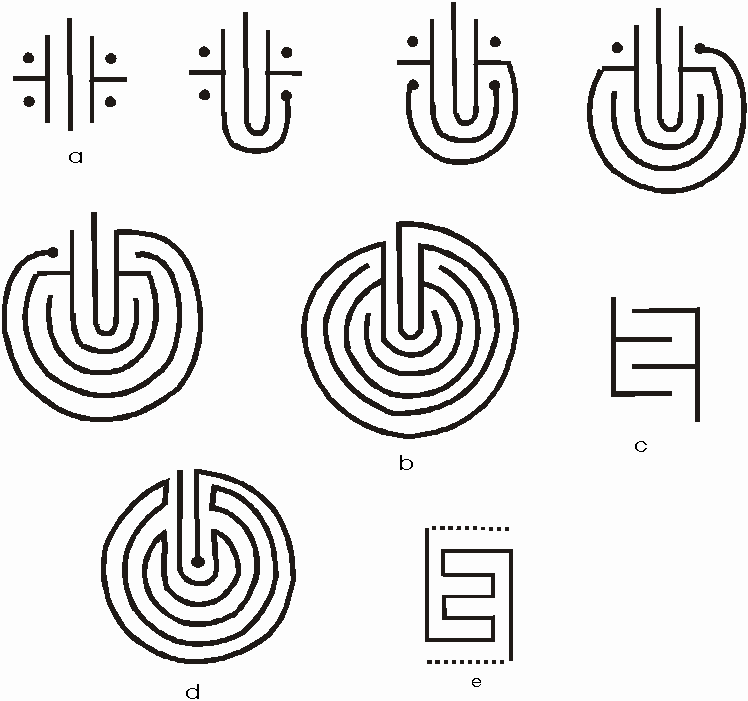
Figure 5: {a} The nucleus. {b} The completed
walls of the labyrinth {c} the dual of the labyrinth
History of the ‘Cretan Labyrinth’ 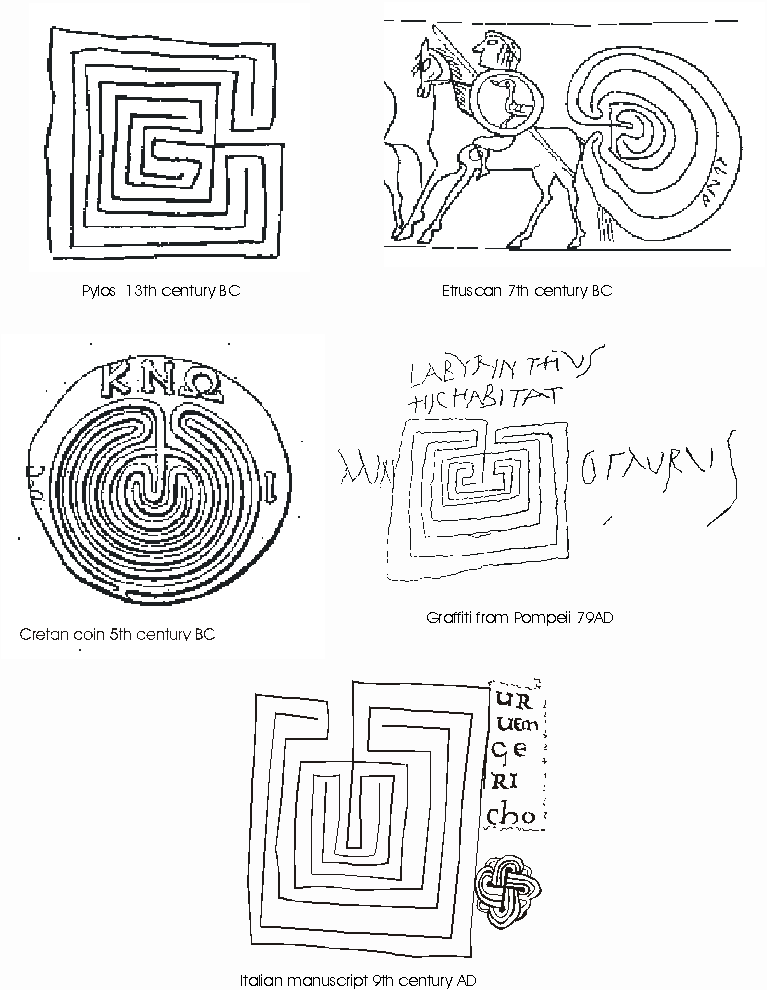
Figure 6: Cretan Labyrinths
The earliest literary reference to the term ‘labyrinth’ is on a small Mycenaean clay tablet found at Knossos, dated c1400BC. The text on the tablet is written in Linear B, a very difficult and archaic Greek. The tablet has been translated to be "One jar of honey to all the gods, one jar of honey to the Mistress of the Labyrinth." [9] The Mistress of the Labyrinth does tend to suggest a goddess. However, goddess of what is the question; a building, a ritual or the cosmos? The tablet leaves more questions than it answers. It is generally thought that the labyrinth is the Palace of Knossos [10] and that the Mistress of the Labyrinth was the Goddess of the Knossos [11]. However, there is no evidence to support this assumption. This symbol has been used in ancient graffiti, rock carvings in England, Spain, Ireland and Sardinia, and they have been dated as early as 2500-2000BC [12], but this dating is without any foundation. The Hollywood Stone, found in Ireland with an inscribed ‘Cretan labyrinth’ was originally dated to the Early Bronze Age. However, on close examination it is now believed to be connected with the early Celtic Church [13]. The earliest dated ‘Cretan labyrinth’ on the basis of archaeological and historical criterion for these symbols is on a clay tablet from the palace of Nestor, Pylos, (Figure 6). Such clay tablets were not meant to be kept as they were originally unbaked. When no longer required the tablets would have been broken up, moistened and reworked to be reused. This tablet only survived because of the fire that destroyed the palace at Pylos, also baked the tablet. The labyrinth tablet was for the scribe’s eye only. The tablet was apparently inscribed with the labyrinth before the writing on the reverse side, and the writing has no relevance to the symbol [14]. It was buried in the ruins of the palace in c1200BC and forgotten until the excavations by Carl Blegen that begun in 1938 [15]. The Pylos labyrinth was no accidental doodle into wet clay by an idle scribe, this labyrinth has an exact and difficult geometrical structure. This structure does suggest that it was drawn from the centre, indicating that a mnemonic devise was used. If it had been an accidental doodle this exact structure would not have reemerged again and again through history. A seventh century BC Etruscan wine pitcher was found in a tomb near the ancient city of Caera, north of Rome. On this wine pitcher is a ‘Cretan labyrinth’ (Figure 6), but this time it is depicted in an allegorical design. The imagery has been equated more or less with the myth of Ariadne and Theseus [16]. The Etruscan labyrinth is round not square as with the Pylos labyrinth. However, these two labyrinths have exactly the same level sequence. The symbol next appears on fifth century BC coins from Crete as a symbol of Crete, (Figure 6). It is often round but occasionally square but these labyrinths have a levels sequence that is the same as that of Pylos and the Etruscan labyrinth. The ‘Cretan labyrinth’ remains on coins of Crete for over six hundred years. This symbol was of religious significance to Crete as shown by the longevity of it being on the Cretan coins. On the reverse side of the coins are divine figures or a bovine head as a symbol of divinity. Graffiti was found on a side of a house in Pompeii, preserved under the lava in 79AD. This depicts a square form of the ‘Cretan labyrinth’ with the inscription Labyrinth. Here lives the Minotaur, [17] (Figure 6) not very flattering for the occupant. Also this exact same structure is found in Biblical manuscripts, as a symbol of the fall of the walls of Jericho, in Figure 6 shows a page of a ninth century manuscript. Next to the labyrinth is the inscription Uruem Gericho, a misspelling of Urbem Jericho, City of Jericho [18]. The ‘Cretan labyrinth’ is in Biblical manuscripts for at least a thousand years [19]. The longevity of this exact and difficult structure does suggest that a mnemonic devise was used. A pottery shard found in Ashkelon in Israel has the nucleus of the Cretan labyrinth (Figure 7.a), [20] it is dated 604BC. This date is so exact because the battle that destroyed the city was recorded Ashkelon was destroy by Nebuchadnezzar, King of Babylon [21]. The pottery shard is of wild goat style originally manufactured in Chios, but this style was manufactured all over East Greece [22]. This is the earliest nucleus of the ‘Cretan labyrinth’ found. But the question has to be asked, ‘Is this a nucleus or just a box type design?’ It is impossible to say. The wild goat style has lot of box type designs and this style of nucleus is not complicated and is easily replicated accidentally. However, such a mnemonic device would explain the duration of this structure across time and cultural diversity. Also a ritual use of this mnemonic device would explain the longevity of the device itself. Furthermore all of these ancient ‘Cretan labyrinths’ are depicted by drawn walls not the path, as if they have been expanded from a nucleus. 
Figure 7: A pottery shard that contains a ‘Cretan
nucleus’
Roman Labyrinths SAT labyrinths are the simplest labyrinths, excluding spirals, the next development in labyrinths are the 'Roman labyrinths' (Figure 8.a). The standard layout of the 'Roman labyrinth' is in four sectors, however this number can be extended, but rarely. These four sectors in the standard layout give an appearance of relatively perfect four-fold rotational symmetry. When you unroll the labyrinth you can see the four sectors (Figure 8.b), the first, second and third sectors are isomorphic to g42 with paths linking the sectors. Definition: In a FF of a labyrinth with semi-axes other than the throat, there are divisions coursed by the semi-axes, which divide the FF into sectors. These sectors consist of a single or a collection of stacked vertically FEs and they are called Fundamental Element Sectors or FES. 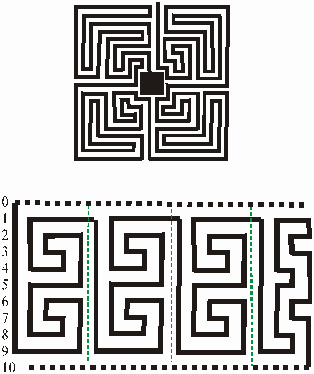
Figure 8: A Roman labyrinth and its FF The fourth FES introduces a new FE that needs to be added to the classification. In Figure 5 there is a FE denoted a2[an] this means, on the right-hand of the graph of the FE anis nested within a a2 FE on the left-hand-side. This type of FE cannot constitute FF alone thus there is no corresponding nucleus. Now the fourth FES in Figure 8 is denoted (a2[a2])2. The notation that will be used for the FF of Figure 8 is R[g42 ´3,(a2[a2])2] this classifies each FES and is read from left to right. In general the notations is R[x ´ i,….,y ´ j] where x ,y = FES and i,j = 1,2,3,..,n. This will enable the variations of each different Roman labyrinth to be detected no matter how many FES there are. 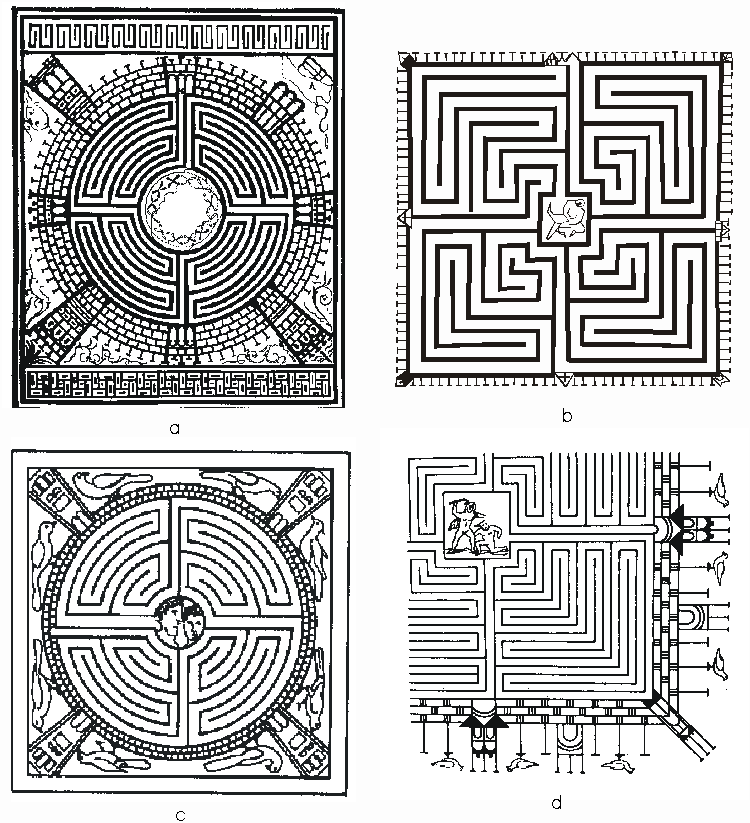
Figure 9: Roman mosaic labyrinths
Figure 9 shows four examples of the Roman mosaic labyrinth, all four examples show the labyrinth as representing a city. Figure 9.a, is dated 200-250AD, and the topology is R[y42x4], in effect this is four ‘Cretan labyrinths’ linked together. The labyrinth represents a fortified city but in the centre of the labyrinth are twelve star-like shapes that possibly represent the twelve signs of the zodiac. This labyrinth could represent the cosmic city. Figure 9.b is dated 25-5OAD, and has the topology R[y42x3, (a2[a2])2], see Figure 8 for its FESs, in the centre of the labyrinth is the dying Minotaur. Figure 9.c is dated 200-250AD, its topology is the same as Figure 9.a, that is R[y42x4]. Figure 9.d is dated 200-250AD and has the topology R[y42x4], each fundamental element sector y44 which is two Cretan labyrinths stacked on top of each other, in the center is Theseus overcoming the Minotaur. Through looking at the topology of the FES, each FES, with the occasional exception of the last sector that runs to the centre, becomes a SAT labyrinth. This makes it easy to see the cultural transference of the symbol and in particular the embedding of other culture’s symbols into another culture’s symbolic format. The structure of the ancient ‘Cretan labyrinth’ remains an integral part of Roman culture. 
Figure 10: The plan of the walls Chartres Cathedral
labyrinth
Church labyrinths The final family of unicursal labyrinths are the 'Church labyrinths' Figure 10, shows the walls of the Chartres Cathedral labyrinth. The FF of the path of this labyrinth is isomorphic to Figure 11.d. The standard layout of the ‘Church labyrinth’ has twelve concentric levels divided into four quadrants. Figure 11 shows examples of the ‘Church labyrinth’ for levels eight, ten and twelve with their FF. By unrolling the Church labyrinth it highlights the symmetry of the structure and will enable the variations of the symmetry and structure of the 'Church labyrinths' to be detected. An example of the notation used for the FFs of Figure 11a is
this classifies each FES and is read from left to right. The bar above and below the middle FESs indicates an extra straight line on the first and last level of that FES. As far as examining the structure goes unrolling the labyrinth is an excellent method but it does not help in look at cultural transferences since there appears to be no connection with the other labyrinth that have been examined. However, if the turns on the semi axes are removed then the SAT structure underlining the Church labyrinth is revealed (see Figure 12). This is far more helpful in tracing the cultural change, transferences and development. 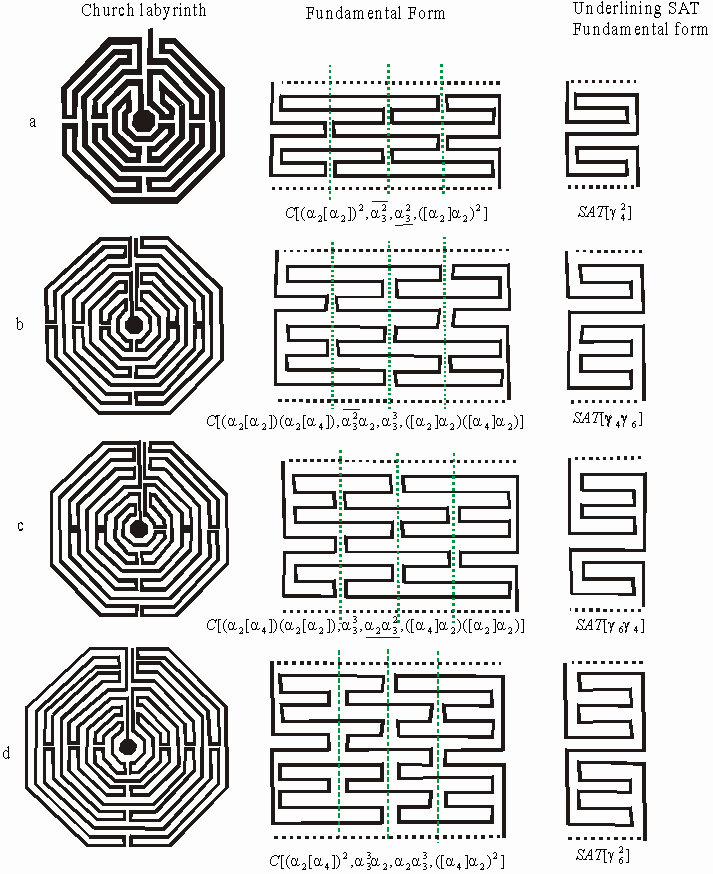
Figure 11: Level 8,10, and 12 Church labyrinths with their FF and underlining SAT FF 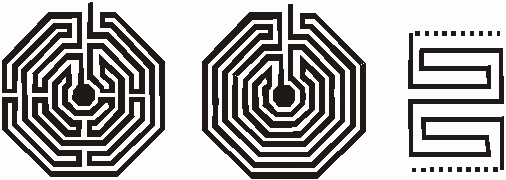
Figure 12: Removing the semi-axes from the level 8 ‘Church labyrinth’
When ‘Church labyrinth’ has eight concentric levels, the level sequence of the underlining SAT labyrinth is 032147658, the ‘Cretan labyrinth’. This is the only variation of the standard ‘Church labyrinth,’ the level ten has two variation, however they are symmetrical to each other. The level eight ‘Church labyrinth’ is a very interesting connection it does give the appearance of having no resemblance at all to the ‘Cretan labyrinth’. The initial thought is that the church labyrinth evolved from the ‘Roman labyrinth’ because of the appearance of the four sectors and closer cultural links. The famous Chartres cathedral, Figure 10, has the underlining SAT labyrinth with a level sequence of 0,5,4,3,2,1,6,11,10,9,8,7,12 two repeated sequences, the FE g6 similar to the Cretan labyrinth FE g4 of only each sequence has a extra turn. All the ‘Church labyrinths’ are all a combination of the FEs of g6 and g4. The twelve levels Chartres style labyrinth is found on the floor of Churches, roof bosses, on stone steles and in many manuscripts, the structure does indicate some continuity with the past. 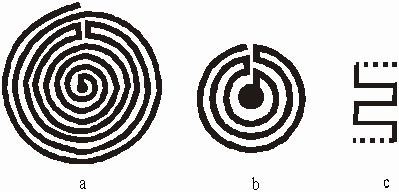
Figure 13: Labyrinth with spirals
Unicursal labyrinths containing a spiral No matter how many levels a spiral
occupies it can be removed without affecting the classification of that
labyrinth since this analysis concentrates only on the turns and junctions.
Figure
13.a has seven levels to the centre, the level sequence is 012345678.
It only has four turns, levels 0->1, 3->4, 4->5 and 7->8. By removing each
spiral the level sequence of Figure 13.b becomes 03478
which then becomes 01234, now the FF is clearly SAT[j4].
Note that in Figure 13.b the spirals have been removed
and the throat of the labyrinth is now clear of paths so it is now possible
to unroll the labyrinth into the rectangular form of the FF.
Conclusion to the restricted unicursal labyrinths topology Through the development of these
three classifications of FF not only can each labyrinth's topology be classified
but also it is possible to make a closer examination of the variations,
structural connections and the transformation from one structure to another,
which can now be highlighted. The continual use of the SAT[g42]
labyrinth indicates that it had a powerful religious or ritual use but
without examining the structure of the labyrinths it would not be possible
to connect the SAT[g42]
labyrinth with the Roman and Church formats. These connections go beyond
the geometrical connection but lead to the cultural and philosophical connections,
which assists in the study of the History of Ideas.
Endnotes [1] Campbell, Joseph. 1991.
Creative Mythology. New York: Penguin Books.
|