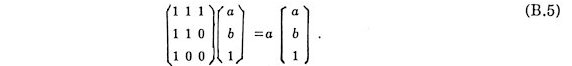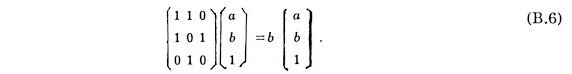|
Appendix Appendix
A
An interpretation is given on the fact that the similarity factor t-3 is the minimum value for three dimensional Penrose tiling with icosahedral symmetry and self-similarity. Six quasibases are a, b, g, x, h, z introduced in Chapter 2. The vectors that can be expressed as a summation of these vectors are restricted as follows. Along a 5-fold axis (parallel to a), it is in the form
and the length is
Along a 2-fold axis (g + z )
whose length is
Along a 3-fold axis (x + h + z )
whose length is
In Table 10, the ratio
of distance to the corresponding minimum value are given for some small
values of (m, n). The ratios 5t and t
can not be realized for 3-fold axis. On contrary,
the ratio t3 can
be realized for all symmetry axes as shown in the last column in Table
10. In order to expand an O6, therefore, the value is the
first candidate of the similarity factor from numerical point of view.
As a matter of fact, the suitable arrangement is actually found as shown
in Chapter 2.
 Table 10 The possible length along
symmetry axis and the ratio to the corresponding minimum value
Let the lengths of two kinds of diagonals of a regular heptagon be a and b where a>b. They are given by
where q = p/7. They are respectively the biggest root of cubic equations
and satisfy the following relations
and
It is noted that the relations are natural extension of that for a regular pentagon
Two sequences
and
associate with them as Fibonacci sequence
does with regular pentagon. Similar relations hold generally for the lengths
of diagonals of regular polygons. The matrices can be regarded as those
for one-dimensional wave propagation.
|