Appendix
A.
Golden
Isozonohedra: A6, O6, B12, F20,
K30
The
definitions of zonohedron and golden isozonohedron are given in the text.
Five golden isozonohedra are A6, O6, B12,
F20 and K30.
These
are two golden rhombohedra A6 and O6. The angle of
two edges at a principal vertex is acute in A6 and obtuse in
O6.
Golden
dodecahedron B12, discovered by Bilinski, can be regarded as
the locus of an A6 or that of O6. It is composed of
2 A6's and 2 O6's. Among 4 quasi-lattice-points altogether,
three are on the surface and the other one inside. The one inside is chosen
of 2 equivalent possibilities. The whole configuration of B12
is four dimensional in the sense that only four kinds of nearest neighbour
vectors are used among allowed six.
Golden
icosahedron F20, discovered by Fedrov, can be regarded as the
locus of a B12. It has a five-fold symmetry axis. It is composed
of 5 A6's and 5 O6's. Among 10 quasi-lattice-points
altogether, six are on the surface and the other four inside. The four
inside are chosen of 10 equivalent possibilities. The whole configuration
of F20 is five-dimensional in the sense that only five kinds
of nearest neighbour vectors are used among allowed six and the one parallel
to the pentagonal axis is excluded.
Golden
triacontahedron K30, discovered by Kepler, can be regarded as
the locus of an F20. It has icosahedral symmetry. It is composed
of 10 A6's and 10 O6's. Among 20 quasi-lattice-points
altogether, ten are on the surface and th'e other ten inside. The ten inside
are chosen of 400 equivalent possibilities. It is the minimum convex region
where all of the allowed six nearest neighbour vectors appear.
It
is noted that the same number of A6's and O6's are
contained in three golden isozonohedra B12, F20,
and K30.
Appendix
B.
The
Coordinates in the Six-Integer Representation
The
configurations with bond orientational perfect long range order of icosahedral
symmetry can be expressed in a form of six-integer-set. It is useful to
introduce proper representation suitable for the purpose. For example,
sometime trigonal and sometime pentagonal.
(1) The trigonal
representation
The
six quasi-bases, a-b-g-x-h-z
are taken so that
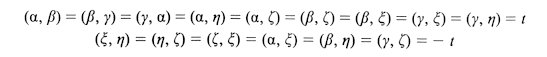
where
t
= cos q
=1 /Ö5.
For
example, they can be taken as follows;
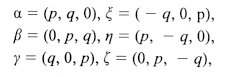
where
p
= Ö((1
+ t )/2 and q = Ö((1
-t
)/2).
There
are following relations among them,
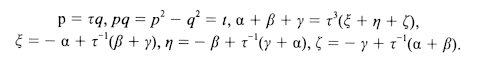
A
representation by these bases is expressed as ( i, j, k,
l,
m,
n
).
(2) The pentagonal
representation
The
six quasi-bases, A -B
-C
-D
-E
-Z
are taken so that
(
A,
B
)=(
B,
C )=( C, D )=( D, E )=( E,
A
)=( A, Z )=( B, Z )=(
C, Z )=(
D, Z )=( E, Z ) = t
(
A,
C
)=( B, D )=( C, E )=( D,
A )=(
E,
B
) = -t
For
example, they can be taken as follows;
A
=
a,
B
=
b,
C
=
x,
D
=
-z,
E
=
h,
and Z
= g.
A
representation by these bases is expressed as [ i, j, k,
l,
m,
n
].
(3) The coordinates
The
coordinates of quasi-lattice-points ate listed in either of these representations.
In
these three choices, if all of three formers or all of three latters are
chosen, then the internal configuration has trigonal symmetry. There are
twenty possibilities in the choice of the trigonal axis. In other six cases
among 23 choices, there are three-times more possibilities for
the direction of axis.
Therefore,
there are altogether 23 × 20 = 160 configurations for
ten inner quasi-lattice-points for a fixed surface configuration. It is
useful for the following discussion to note that seven trigonal surface
quasi-lattice-points among twenty are occupied by the principal vertices
of the inner O6's and one among the seven can be on a trigonal
axis.
In
the case of a triacontahedral cage in the skeleton of an expanded A6,
an O6, which separate the cage into two parts, is already fixed.
Then, only nine inner quasi-lattice-points have freedom and the number
of configurations is reduced to as 23 × (1 + 3 + 3 ×
3) = 104.


NEXT
VisMath
HOME
|