|
GRAPHICAL GEODESIC LINES
APPLIED
TOHRU OGAWA
and YOSHINORI WATANABE
Institute of Applied Physics,
The graphical geodesic
line (GGL) is a tool of characterizing some feature in intermediate
range order of 2D structure. In 1990, the GGL analysis of the triangulated
Penrose tiling was perfectly carried out by one of the authors (TO) and
R. Collins. Now it is applied to the octagonal quasiperiodic tiling. The
situation is different from the former case and a kind of chaotic behavior
in a digital space takes place.
1 Introduction The concept of graphical geodesic line (GGL) was introduced by Ogawa and Collins [1] in 1989 to characterize the intermediate range feature of any 2D triangular networks. A graphical geodesic line is defined as a sequence of triangles, adjacent elements of which shares an edge in common and the common edges in a GGL form a zigzag line. It is locally straight but may globally meanders. For a regular triangular lattice, whole set of the geodesic lines consists of three sets of periodic arrangement of parallel straight lines. Generally speaking, behavior of geodesic line is classified into two cases; open and close, in other words infinite and finite. In both cases, it may or may not cross itself. The length of a graphical geodesic line is measured by the number of triangles it passes. For N (® ¥) points, the number of the triangles is 2N and the total length of the graphical geodesic lines is 6N. A GGL is expected as a path of a free particle. They successfully applied the concept
to the triangulated Penrose tiling. Their result is summarized in Section
3. In this paper, the method is applied for octagonal quasiperiodic
tiling whose elements are square.
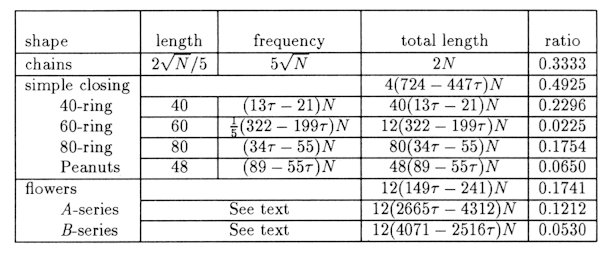
2 Some Properties of GGL A GGL, which was defined in the previous section, runs locally straight and globally meanders because of local curvatures of the space or the fluctuation of the coordination numbers. Here the local curvature corresponds to the distribution of vertex coordination numbers. In view of this fact, it is useful to define the excess coordination number DR of vertex R as DR = ZR - 6 where ZR is the coordination number of vertex R. For a regular triangular lattice where the coordination number of any vertex is six and their excess coordination numbers are all zero. Geodesic lines are three sets of parallel paths. The GGL's tend to converge (diverge) in the presence of a vertex with negative (positive) excess coordination number. If two geodesic lines never intersect, the total excess numbers of all the vertices in the infinite region between them is non-negative. Table 1: The Classification of GGL in 2D Triangulated Penrose Tiling.
Two geodesic lines may intersect each
other several times. There are three types of closed regions bounded by
two geodesic lines. There are three types of closed regions bounded by
a single curve. The bounded regions in these cases are systematically analyzed
in terms of the total excess coordination numbers in the region [1].
3 GGL in 2D Triangulated Penrose Tiling A triangulated Penrose tiling is obtained
by drawing the minor diagonal of all the tiles of the rhombic version of
2D Penrose tiling. Ogawa and Collins succeeded in the complete analysis
of the triangulated Penrose tiling in the sense that all the possible shapes
of the lines and their frequency of appearance rigorously. The analysis
revealed some very organized hierarchical structure of the network with
self-similarity. The result is summarized in Table 1.
The lengths of A-series flowers are expressed as 165×4n
+ 540 (n = 1, 2, 3,...), explicitly, 1200, 3180, 11100 42780, ...
and their frequencies are 1/5(47 - 29t)t-4(n+1)N.
The lengths of B-series flowers are expressed as 330×4n
- 540 (n = 1, 2, 3, ...), explicitly, 780, 4740, 20580, 839401 ...
and their frequencies are 1/5(18 - 11t)t-4(n+1)N.
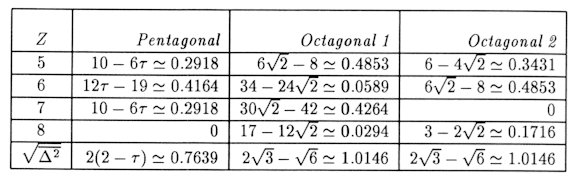
Table 2: Comparison of the Three Triangulated tiling.
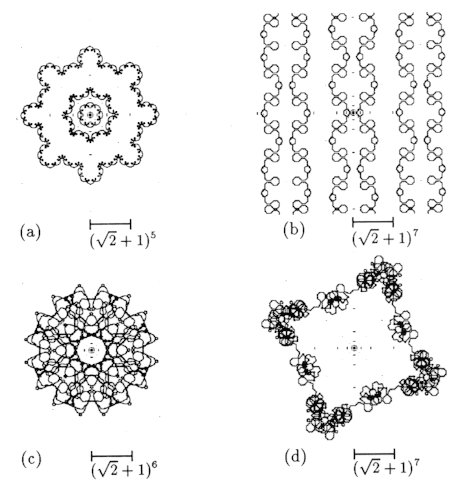
4 Octagonal Quasiperiodic Tiling Octagonal quasiperiodic tiling was discovered by several people including one of the authors [2, 3]. The elements are square and 45o-135o rhombus and whose composition is (Ö2 - 1) : (2 - Ö2) = 1 : Ö2 respectively. The variety of arrow convention for edges is only one kind. There are two ways of the triangulation for square tiles, one of whose diagonals is the symmetry axis. The first one may be described as the symmetry axis is the major diagonal of the square and it corresponds to the minor diagonal in the second one. We tried the former case (Octagonal 1), where the symmetry axis corresponds to the major diagonal of a rhombus, first and this paper is a preliminary report of the attempts. The comparison of the three triangulated tiling are summarized in Table 2. The main results of observation are given below. 1. The number of the points of ZR = 6 is extremely small in Octagonal 1. Therefore GGL's tend to go rather straight, and then are scattered strongly. There are many pairs of slightly meandering GGL's which are rather straight and sometimes they swap the partner when such pairs come across. 2. Some connection of new type starts at rather large scales. In such cases, some connectivity of elementary local GGL elements arises which does not happen in smaller scale. 3. There are many simple closing lines. Their variety is far more abundant than pentagonal case. The amount of the GGL which we traced is nearly 80%. Two types of infinite hierarchical GGL's are contained among them. The lengths of A-series (Figure 1 (a)) are 273×3n = 816,2448, 7344,. ..., and their frequencies are (Ö2 - 1)2(n+4)N. The lengths of B-series are 22752×3n-7536×(-1)n = 75792,197232,621840, and their frequencies are (Ö2 -1)2(n+8)N. 4. There are chains (Figure 1 (b)), which are open GGL's with 1D-extension. Those are self-crossing but macroscopically straight. There are four sets of parallel GGL's. There are only two separation widths, (Ö2 + 1)7 and (Ö2 + 1)7/Ö2 , for two successive parallel GGL's. 5. There remain
rather many GGL's of big scale and of new type (Figure
1 (c)(d)). It is very difficult to deny the possibility of such a new
connectivity. From these, we are thinking of the possibility of a kind
of chaotic behavior.
Figure
1: Examples of GGL in the case of Octagonal 1. (a) Infinite
hierarchical GGL's
References [1] T. Ogawa and R. Collins, Chains, Flowers, Rings and Peanuts: Graphical Geodesic Lines and Their Application to Penrose Tiling, in Quasicrystals, ed. T. Fujiwara and T. Ogawa (Springer Verlag, 1990). [2] T. Ogawa, in Science on Form, ed. Y Kato et al (KTK Scientific and Reidel, 1986). [3] T.
Ogawa, Symmetry of Three-Dimensional Quasicrystals,
Materials Science Forum 22-24, 187 (1987).
The original paper is published in Proceedings of the 6th International Conference on Quasicrystals (Eds.: S. Takeuchi and T. Fujiwara, World Scientific, 1998). |