In Wave Space, the geometry defines the space. The elements, which are shapes in themselves, as squares inCartesian space, are the increments of Wave Space. To get an idea of how shapes change from geometry togeometry. Let us take a 2×2, 4 element square, and translate it in the following two geometries: Fig. 3.1 showsthe square in three regions of the CWS geometry G(X₁4/4Y₁4/2); here, the square appears as a rather amorphousblob, one shape being almost linear in its elongation. Fig. 3.2 is an example of IWS geometry G(X₁2X₂^p22/2),which converts the Cartesian square of our space into a 4 element circular shape in Wave Space,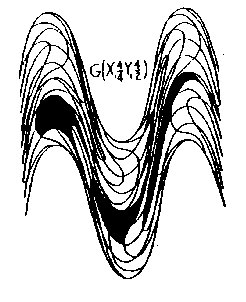

Figure 3.1 CWS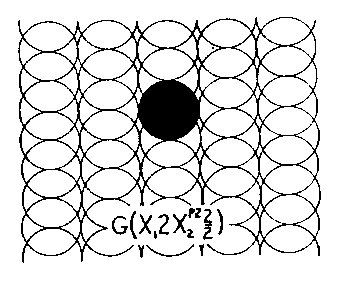

Figure 3.2 IWS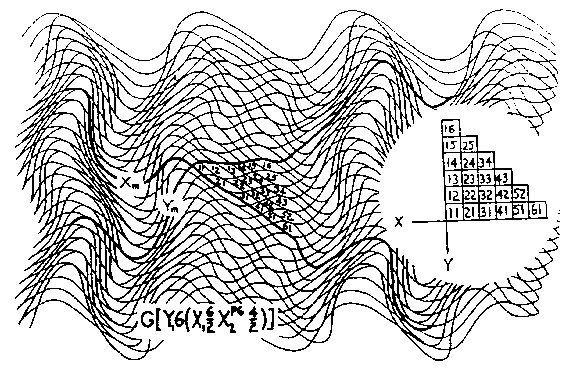

Figure 3.3 Translation

What we have done is take a square from our reality and put it in a different geometric reality. In a sense, it is still a square, and would be seen as such by the inhabitants of this new geometric space; however, from our frame of reference, it has become a circle. In this kind of physicality, it begs the question: What is "true" shape? The answer would seem to depend on your frame of reference, which is true; and, in this particular case, it depends on the geometric space the object occupies. Physically and philosophically this is interesting - considering the infinity of spatial configurations possible; that is, of course, if such spatial realities exist, a speculation we will consider later.

As an exercise, if we wish to translate from our Cartesian space to a Wave Space geometry, refer to Fig. 3.3. Here, we have a geometry similar to Fig. 2.5 with our mock axes arbitrarily chosen, as shown, and numbered to parallel our Cartesian grid (inset). It is now a matter of drawing a shape in Cartesian space and converting it to Wave Space, or do the reverse to see what shapes created in Wave Space look like in Cartesian space. For a demonstration, I show an imaginary character from Cartesian space, Fig. 3.4, and show it in three other geometric configurations,  Figs. 3.4a, 3.4b, and 3.4c.

Figure 3.4 Character 

Figure 3.4a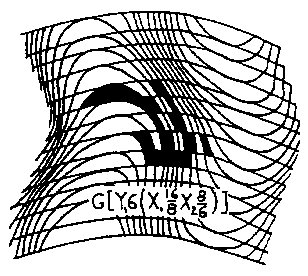 

Figure 3.4b 

Figure 3.4c

However, the idea of shapes changing outside our frame of reference is not new when we consider Einstein's illustration of a clock approaching the speed of light: From our frame of reference, we see the clock being flattened and time slowing; but, from the clock's frame of reference, evenything has remained normal.

If we assume a shape to move in Wave Space, some curious things occur. A shape moving in our Newtonian (Cartesian grid) space will maintain its dimensional and geometric integrity. A shape moving in CWS will distort to a greater or lesser degree, depending on the geometry of the space it traverses; but the relationship of the elements will remain the same. However, a shape moving in IWS will not only distort, but it may fragment; that is, on an elemental level, the relationship of the elements will not remain intact. In IWS, the elements in a shape following one of the mock axes will keep a consistent relationship with one another regardless of the degree of distortion of the shape, as is shown in Fig. 3.5a. Here, we have our 4-element square following the X_m axis through a number of successive incremental changes. If the shape should follow a specific phase track exclusively, as is the case in Fig. 3.5b, some of the elements will separate (the cross-hatched figures) from their partners while passing through the nodal region; however, the square will be reformed as it passes through the next nodal region, thus following a cyclical process of fragmentation and reformation from region to region. For larger shapes comprising a vast number of elements, the individual incongruities would most likely be absorbed and seen as proportionally minor disturbances, fluctuations, or pulses.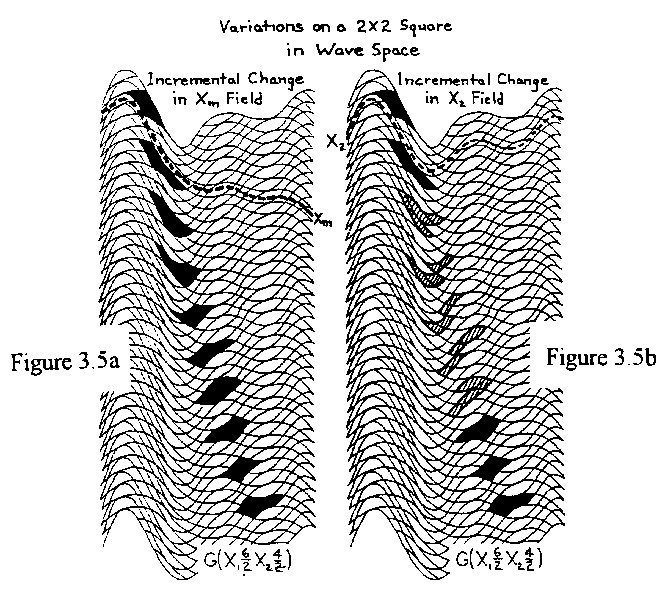

Figure 3.5a         Figure 3.5b
 
 
 

NEXT