|
Of Torus and Turk’s-Head Knots: A Polar Trigonometric Modeling By Skip Pennock
This article concerns itself with graphical solutions from an artist’s/ craftsperson’s/ knot tyer’s perspective. The knots depicted may actually be tied utilizing the
diagrams contained herein, although a good many of the knots may also be
tied “in the hand,” as a sailor/ boater would say, because these knots
are kept relatively simple for illustrating purposes.
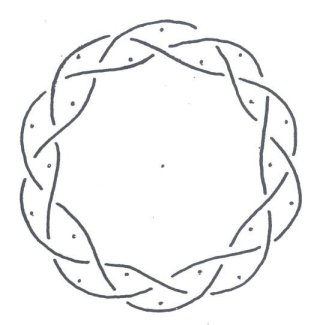
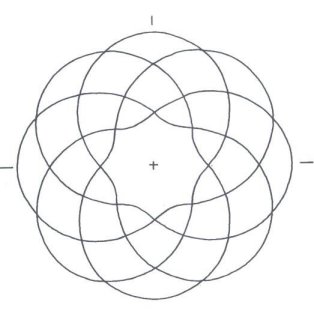
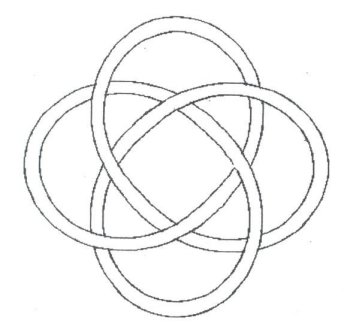
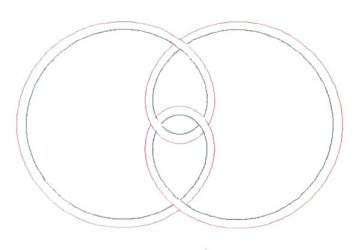
You are very likely to know more about mathematics than I will ever know. I apologize, taking into account your knowledge. In all probability this work has been done before my attempts. It is simply that I do not know of these other attempts, and have never seen these graphs before, elsewhere. The mathematics presented herein, I should say, consists of many anecdotal cases, for, not being a true mathematician, I do not know how to generalize them into a formal proof. Figure 1 shows an additive model applied
for the centerlines of two very simple Turk’s-Head knots. The equations
are also very simple. If the radius R = a constant (in this case,
2 units), then we have the graph of a circle. If an appropriate wave is
added to the circle, then we will have a wavy, braided graph with the right
number of Bights and the right number of Leads.
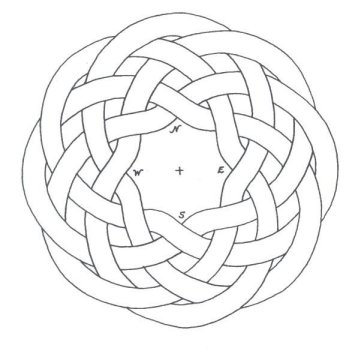
Figure 1
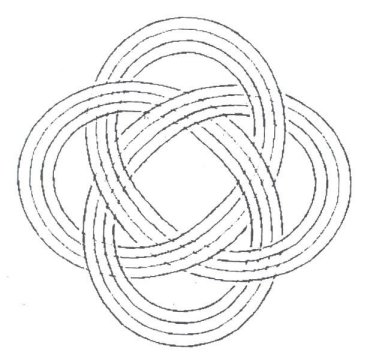
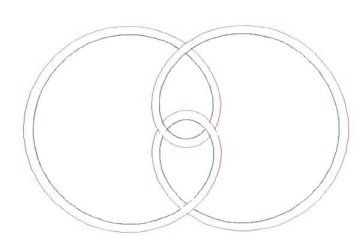
In these cases, a Cosine wave was chosen, because, at its start where q, q = 0o, (or q = 0 Radians), there will be a maximum, and an axis (or orthogonal plane) of symmetry. q ranges between 0 (0 radians), and the Number of Leads × 360 degrees (#Leads × 2p radians). The Amplitude of the Cosine wave was set to = an implicit 1 unit, for reasons of simplification. Some definitions concerning “Turk’s-Head Knots,” “Bights,” and “Leads” (pronounced ‘leeds’) are in order here. To be respectful, a word about the nomenclature “Turk’s-Head” knots, for were I of Turkish lineage, I might be offended by the term: The name first appeared in the literature in Darcy Lever’s 1808 publication The Sheet Anchor , according to Clifford W. Ashley, in his comprehensive and unequaled to date publication, The Ashley Book of Knots. Ashley goes on, saying Their resemblance to turbans was presumably the reason for the name, and There are no knots with a wider field of usefulness. The family of Single Piece, or Common, or Running Turk’s-Head knots, as they are now known almost universally, is one of the most attractive series of knots ever devised or discovered. They are quite ancient, with representations of them being carved into columns found in Egyptian Pharaonic tombs, for example. They are usually cylindrical in form, but they can be tied in decorative and practical woven flat knotting form. Besides consisting of single lengths of cordage, once they are finished, they are “Alternating” knots with a regular over/under, sometimes termed “Basket” weave, pattern. A “Bight” is defined as a scallop or curve at the rim of the knot where the cord changes direction. Given a Common, Running Turk’s-Head knot, there is only one number of Bights. For a flat knot, if you count, the number is the same around the inside hole as around the outside rim of the disk formed by the knot. For a cylindrical knot, the number at the top of the cylinder always equals the number at the bottom. A “Lead” is defined for a Turk’s-Head knot as a single path or revolution of the cord around the band, or if a flat knot, around the hole in the center of the disk, while discounting the extra “parallel” threading or following of the original knot when an extra “Ply” or two is put into the knot. (Sailors call putting an extra ply or two into a knot, “doubling” and “tripling” or, “doubling twice.” A little confusing terminology and tradition.) Given a Turk’s-Head knot, there is only one number of Leads. Figure 2 shows a Turk’s-Head knot tying
diagram, which was created for use with copper twist wire. For knots which
are tied of softer material, such as most cordage, this knot may be made
without resort to nails, pins, or diagram, and may easily be tied in the
hand.
Figure 2
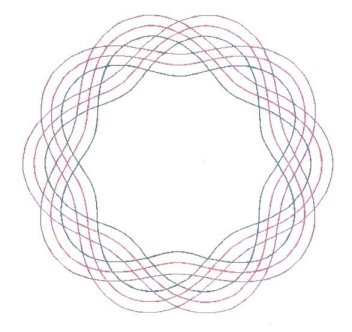
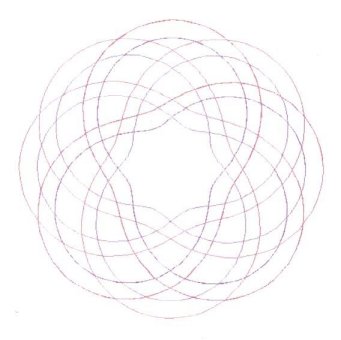
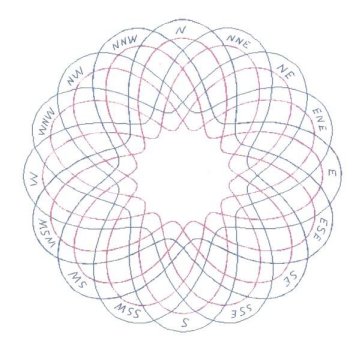
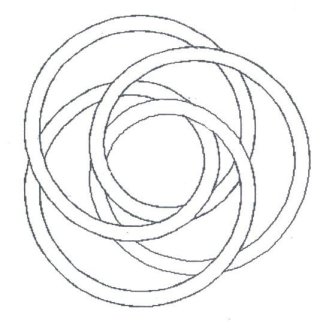
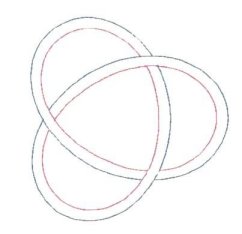
Depending upon how one views graphical representation,
Figure
3 either shows a doubled or tripled centerline diagram.
Figure 3 is actually three equations,
expressed together as one, through the usage of braces. And just as in
Figure
2, there are 10 Bights and 3 Leads.
Figure 3
Something that needs mentioning is that in all the models of Running Turk’s-Head knots in this article, and all known of, the number of Bights and the Number of Leads may have no common factor (or, divisor). The models explain this phenomenon. If they do, in the models, the factor will cancel out in both the numerator (#Bights) and the denominator (#Leads). In such a case the resulting modeled knot will have both fewer Bights and fewer Leads, and it may not form a braided knot at all, but rather, the Unknot. It should be apparent that the generalized model used thus far is: Radius = Rmid + (Amp × Cosine ( B × T / L )) Where: Rmid is a Midrange radius constant, which is greater than
Amp;
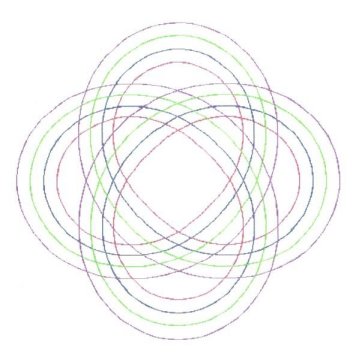
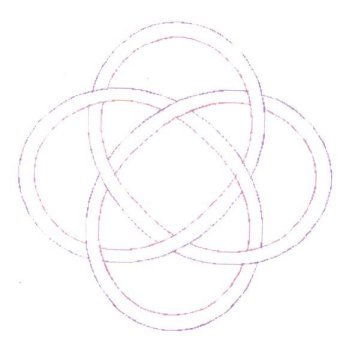
Something which is surprising, is that very often, not only can Rmid be Added to the parenthetic Cosine function, but Rmid can be Raised to it. Figure 4 and Figure 5
demonstrate this. In these cases, Rmid is not actually a true midrange
value.
Figure 4
Figure 6 and Figure 7
show the versions of some of the first, additive models the author arrived
upon while taking a Calculus I refresher class at Towson University. One
day after class, the Professor asked, “What are all those pretty little
geometric drawings you make during class?” I explained and she suggested
I utilize Polar Coordinates directly, instead of trying to convert over
from the more familiar Cartesian Coordinate System. Figure
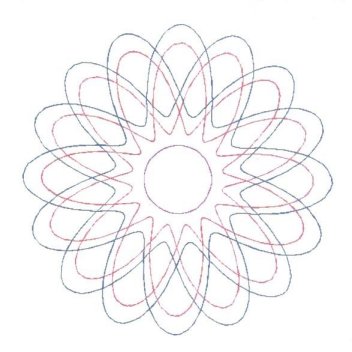
8 is the most recent personal result for an 8-Bight, 5-Lead graph.
Figure 6
Figure 7
Figure 8
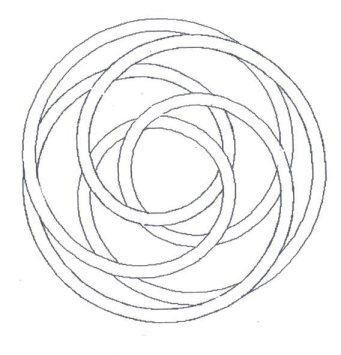
Figure 9 & Figure
10 are just for the fun of it.
Figure 9
Figure 10
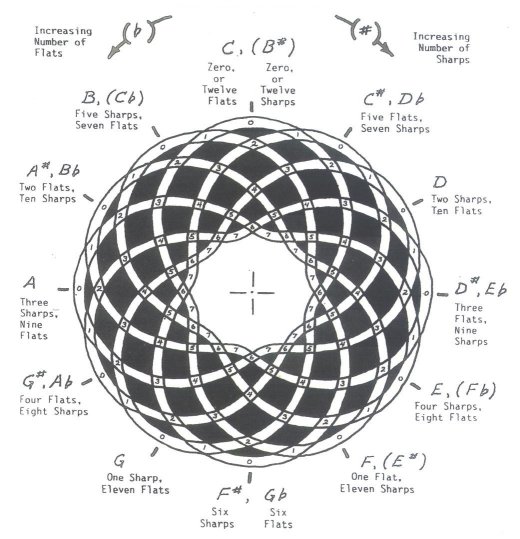
Figure 11, as it says, works much like a clock. It explains just about all that the author knows about Music Theory, which is not a whole lot, but attention should be paid to the written part at the bottom of the figure. Here is an interesting application of a Knot to Music Theory. It works much like a clock. CYCLE of "FIFTHS"
Figure 11
It only recently occurred to the author how well it would be possible to make usage of the polar trig models for Torus knots, for it soon becomes obvious that the crossing sequences neeed not be alternating on these graphs. Figures 12-16 are a couple of results.
Figure 12
Figure 13
Figure 14
Figure 15
Figure 16
Figures 17-20 demonstrate a set of
possibilities which arise from using the polar trig model, a 2B,
3L Power Curve. Which brings us back full circle, to the beginning.
Figure 18
Figure 19
Figure 20
However, before finishing this article, the author must
restate the old adage that “Knots are a book which has no end,” and leave
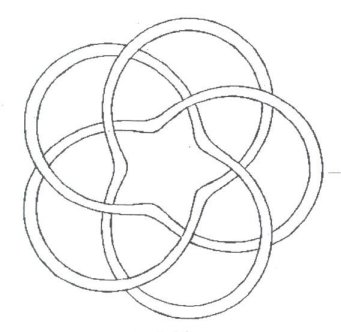
off with a couple of personal artistic designs in Figures
21-22.
* * * The author would like to thank Professor Slavik Jablan for all he has done in converting the paper graphs to electronic format, and for composing the material. The author would also like to thank Rosalyn R. Carpenter and Thomas M. Hughes for their assistance in proofreading and readibility of this article. The author would like to thank Professor Ann Wagner of Towson University for her encouragement and suggestions regarding polar coordinate graphing. Aside from searching the Internet, to no avail, for graphs similar to the ones presented in this article, the author would like to cite the following two texts as sources: Adams, Colin C., The KNOT Book, An Elementary Introduction to the Mathematical Theory of Knots, W.H. Freeman and Company, New York, New York, 2001. This book was given to the article’s author by Phyllis J. Robinson. Ashley, Clifford W., The Ashley Book of Knots, Doubleday & Company, Inc., Garden City, New York, 1944. A copy of this book was given to the author by Wallace McCurdy and Family, including Martha. Skip Pennock,
|