|
PROPORTIONS IN POLYGONS Mª ENCARNACIÓN REYES IGLESIAS
Name: Mª Encarnación Reyes Iglesias, Mathematician, (Burgos, Spain, 1954). Address: Departmento de Matemática Aplicada Fundamental, E.T.S. Arquitectura. University of Valladolid Spain. E-mail: ereyes@maf.uva.es Fields of interest: Geometry, proportion, symmetry
(Art and Architecture, Mathematics with Paper Folding, Phyllotaxis, and
Mathematics in Daily Life).
Publications and/or Exhibitions: - Proporciones y Arquitectura. ICME, (Congreso Internacional de Educación Matemática) Sevilla 1996. - Estudio y desarrollo geométrico del Modulor de Le Corbusier, VIII JAEM, (Jornadas Nacionales para la Enseñanza y Aprendizaje de las Matemáticas.) Salamanca 1997. - Proportions mathématiques et leurs applications a l' architecture. Bulletin IREM (Institut de recherche pour l'enseignement des mathématiques de Toulouse) Toulouse. France, 1998, 39 pp. - Papiroflexia y proporciones dinámicas en rectángulos. JAEM (Jornadas Nacionales para la Enseñanza y Aprendizaje de las Matemáticas.) 1999 - Mathematics: a determinant strategic for the development
of an architectonic project. Symposium on Symmetry. Alhambra 2000,
Granada (Spain)
Abstract: In this exposition
I will focus mainly on the concept of Polygonal Proportion, (PP). At the
same time I present some constructions of polygons using paper folding.
It is very important the justification of these constructions with mathematical
operations. Teaching mathematics through paper folding is becoming a methodological
way understanding mathematics. Today many average citizens usually only
remember traumatic classroom experiences related with the process of learning
mathematics. One of the purposes of this paper is defining a common message
to improve the image of mathematics in contemporary society. Sharing properly
designed activities and classical proofs can help a long way towards fruitful
and productive mathematics education Teaching mathematics has been enriched
with using paper folding environments of exploratory type where students
can experiment with geometrical objects, investigate their properties,
formulate conjectures and verify them.
The concept of proportion in segments and rectangles is well known, but the polygonal proportion (PP) is a concept not so readily studied. We define the proportion of polygon Pn, written p(Pn), as the quotient between the area of the polygon and the minimum side square. In case of a square this formula give us 1 and if R is a rectangle whose sides are a and b, a>b, we obtain p( R ) = (ab)/b2= a/b. This definition applied to the regular octagon O8 provides: p(O8)=2(Ö2+1)=q, where q denotes the silver number. After establishing the definitions and their main properties, we can pay attention to geometric relations in some of convex polygons. The ratio between the radius of the circumscribed circumference of a polygon and the side of this corresponding polygon, is very important. In the case of the decagon, this relationship gives us the golden section and in the case of the octagon, the "cordobesa proportion". Every case of polygonal proportion can be illustrated with many examples in: 1.- Art: classical and modern
paintings as well as ultramodern painters.
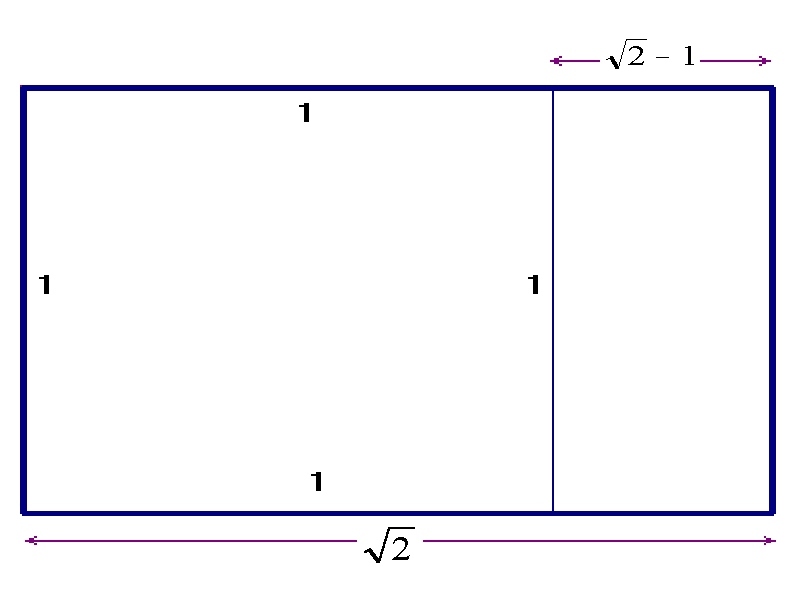
Related with educational aspects I think the paper folding is an important tool when it is incorporated in classes in all levels. My interest focuses on research the underlying mathematics involved in paper folding process. I will construct some of the polygons by paper folding, justifying their constructions with mathematical operations. I will prove that it is possible to obtain an octagon starting from an A4 sheet of paper. It is well known that the DIN A 4 format has the proportion Ö2.So we can consider 1×Ö2the dimensions of the paper.
If we cut the gnomon of a DIN A4, e. g. one square, we
have a little strip of dimensions 1×(Ö2-1).
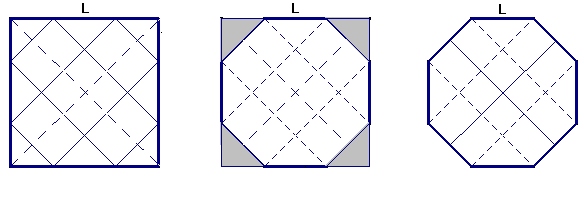
Therefore the strip of paper is placed in parallel with the diagonal of the square and tangent to its sides. Repeat same operation with the other diagonal of the square. Folding the corners of the square, we obtain the regular octagon. The proof of this result is the following:
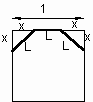
Denoting by L the side of an octagon obtained from a square whose side is 1, we have: 2x+L=1 ; L2= 2x2; x2 = L2/2; x=L/Ö2; 2x+L= 1 Û (2L/Ö2)+L=1; (Ö2+1)L=1; L=1/(Ö2+1)=Ö2-1. Then L = Ö2-1. What implies that the paper folding process is correct
because the side algebraically obtained of the octagon has exactly the
same value as the side of the octagon obtained from the smallest side of
the strip. Because the proportion in a pentagon is related with the golden
number f, the format of DIN A4, in proportion
Ö2
is not suitable for the pentagon. We'll use the paper size's proportion
combined with the Polygonal Proportion to make constructions of some polygons
and justify them algebraic and geometrically.
References Alsina, C. Trillas , E., Lecciones de Algebra y Geometría para estudiantes de Arquitectura. Ed. Gustavo Gili, Barcelona, 1981. Hargittai, I. , Fivefold Symmetry, Ed. World Scientific USA, 1992. Jean, R., Barabé, D. Symmetry in plants. Ed. World Scientific, 1998. Kappraff, J., Connections. The geometric bridge between art and science. Mc Graw Hill, New York, 1991. Kappraff, J. Systems of Proportion in Design and Architecture and their Relationship to Dynamical Systems Theory. http://members.tripod.com/vismath/kappraff/ Reyes, E. Formatos DIN y papiroflexia de algunos polígonos. 5º Seminario Castellano-Leonés de Educación Matemática. Zamora (Spain) 1998. Reyes, E. Papiroflexia y proporciones dinámicas en rectángulos. JAEM (Jornadas Nacionales para la Enseñanza y Aprendizaje de las Matemáticas.) 1999. Spinadel, Vera W. De, The metallic means family and multifractal spectra. Non Linear Analysis, 36 (1999) 721-745. Spinadel, Vera W. De,
. From the Golden Mean to Chaos, Ed. Nueva Librería, Buenos
Aires, Argentina,1998.
|