|
Carlos E. Puente and Marta G. Puente Hidrology and Institute of Theorethical Dynamics
Name: Carlos E. Puente, Mathematician and Engineer
(b. Cartagena, Colombia, 1956).
1. INTRODUCTION Recently, new constructions of the univariate and bivariate Gaussian distributions have been introduced by .1,2 These are universal representations based on plane- and space-filling fractal interpolating functions,3 constructed via iterations of simple affine mappings, that transform arbitrary diffuse measures (i.e., with continuous cumulative distributions) into bells. Also, it has been discovered that the new construction of the bivariate Gaussian distribution leads, as the iterations are performed, to a host of exotic kaleidoscopic patterns of a transient nature having arbitrary n-fold symmetries, that decompose the circular bell in unforeseen and remarkable ways.4,5 The intrinsic beauty and apparently infinite variety of snow crystals have fascinated and puzzled mankind for centuries. Studied by renowned thinkers such as Kepler, Descartes, and Hooke, and amply photographed in the first half of the twentieth century by Bentley and Nakaya, these lovely sets continue being researched under natural and laboratory conditions.6 Although much has been learned about the diverse shapes formed under distinct climatic conditions,7 their modeling remains a challenge due to the intricacy of their geometries.8 The purpose of this article is to show that the circular bell contains a vast collection of 6-fold symmetric patterns that encompass the graceful geometric structure encountered in many ice crystals, including both stellar and sectored flakes of diverse varieties. The organization of this paper is as follows. Section
2 reviews the mathematical construction leading to the exotic patterns
that make up a circular bell. Section 3 shows that specific ice crystals,
taken from Bentley's catalog, may be closely
captured via suitable iterations of two simple mappings, as members of
a gigantic jigsaw puzzle that ultimately generates a circular bell. This
section also presents several examples which illustrate the sensitivity
of the patterns to the specific iterations followed. Section 4 portrays
yet more examples of "ice crystals'' "grown'' inside the bell via fractal
interpolating functions and more general attractors, when the iterations
of two suitable maps are performed following the binary expansion of p.
The article ends with its concluding remarks.
2. THE EXOTIC PATTERNS INSIDE THE CIRCULAR BELL The graph G of a continuous fractal interpolating function over three dimensions, a "wire'' from x to (y, z), passing by N+1 points {(xn, yn, zn): x0 < ¼ < xN}, is defined as the fixed point of N contractive affine maps, G = Èn = 1N wn(G), where
subject to
and such that
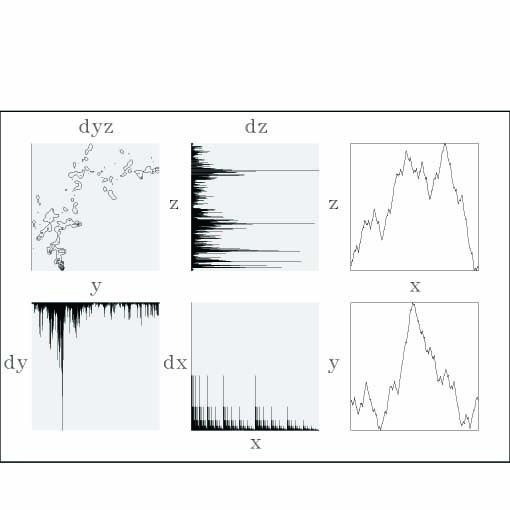
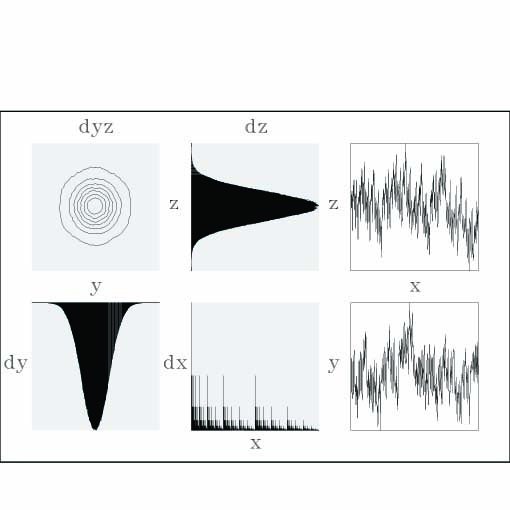
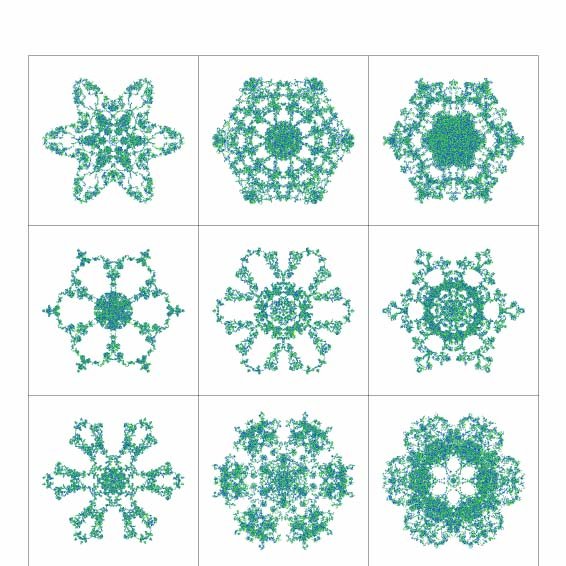
has L2 norm, Ö{lmax (AnT An)}, less to one. Equations (2) ensure that G contains the initial points and allow computing parameters an, cn, kn, en, fn, and gn in terms of the N+1 interpolating points and the scalings rn(j) and rotations qn(j), via simple linear equations. At the end, the unique, and hence deterministic, set G turns out to have fractal dimension D Î [1,3), and a space-filling fractal interpolating function is obtained when the L2 norm of matrices An tends to one, that is, when all |rn(j)|® 1 and qn(1) = qn(2) + k p, for any integer k.2 In practice, the graph of a fractal wire is found dot by dot, starting the process at a point already in G and progressively iterating the maps wn following the outcomes of independent "coin'' tosses.9 As this process is carried, a unique invariant measure is also induced over G, and unique (deterministic) projections of such a texture over the coordinates x, y, and z, say dx, dy, and dz, and jointly on the y-z plane, dyz, may be obtained to visualize how the attractor is filled from a variety of vantage points.1 Depending on the usage of fair or biased coins and on the actual placing of the initial points in x, dx is either uniform or (multinomial) multifractal and dy, dz, and dyz are derived measures of dx via the marginal and joint functions implied by the continuous fractal interpolating function.1 Figure 1 shows examples of these notions for two such fractal functions that interpolate {(0,0,0), (1/2,1,1), (1,0,0)}, and whose implied affine mappings have all rotations equal to 60 degrees, and scalings -r1(1) = r1(2) = r2(1) = r2(2) = r such that r = 0.55 (top), and r = 0.9995 (bottom). Included in the plots are the implied aforementioned projections of the unique texture over G (left) and the x-y and x-z projections of the function itself (right), as obtained when the two required mappings w1 and w2 are used on a 70-30% (biased) proportion, for a total of 15 million times, using pseudo-random numbers to guide the iterations,10 starting from the mid-point (1/2,1,1). Notice, on top, how the conjunction of the induced (binomial) multifractal measure dx and a low-dimensional transformation leads to interesting derived measures dy and dz that resemble data sets as found on a variety of applications.11 Observe, in the bottom, how the (joint) derived measures tend to a bivariate Gaussian distribution with no correlation, as D ® 3, a result that happens to be universal, for the shown dx may be replaced by any diffuse measure to obtain yet another bivariate Gaussian (possibly with non-zero correlation) over the y-z plane.2 As recently discovered, when the outcomes of few thousand points at a time are plotted rather than several million, the iterations generate unexpected and exotic patterns over y-z.4,5 Figure 2 illustrates such results by showing successive sets made of 20,000 points as found from the same set-up of Figure 1 but with r = 0.99995, which result in 6-fold (360/60) symmetric patterns. Notice how the limiting circular bell is decomposed in
terms of beautiful mathematical designs of diverse shapes, colored green
and blue according to mappings w1 and w2,
unforeseen kaleidoscopes which suggest that the geometric structure of
actual ice crystals may be understood in terms of suitable iterations of
simple mappings. That such may be the case is studied in the remainder
of this work.
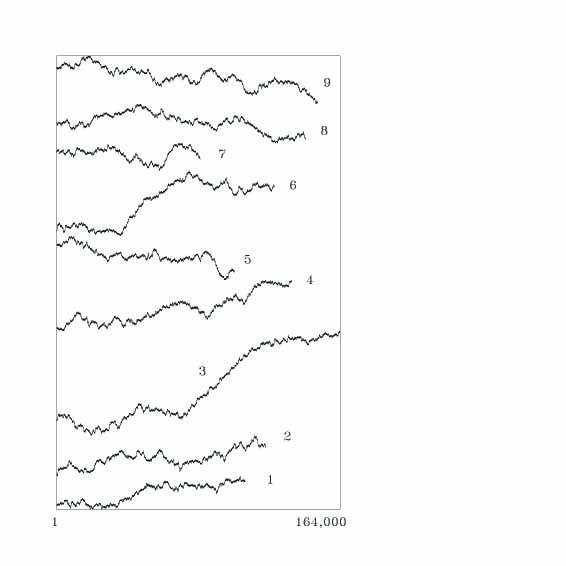
3. EXAMPLES OF ICE CRYSTALS INSIDE THE BELL To study whether actual snow crystals may be encoded geometrically as geometric objects inside the bell, a collection of sets from Bentley's famous catalog was selected. Then, computer templates of such varied patterns were made in order to assess the existence of suitable iteration paths that would allow filling them point by point, using two simple affine maps that ultimately yield a circular bell. Figure 3 shows that such an exercise indeed proved successful, pasting together appropriate sequences of heads and tails in groups of a 1,000 tosses, as given by a generic pseudo-random numbers generator,10 using a fair coin. Specifically, all such sets were found using the same nearly space-filling fractal function, one that has the same set-up used before except for the magnitude r = 0.99999. At the end, all ice crystals turned out to be members of the same bell but required alternative iteration paths which, as shown in Table 1, ranged from 83,000 (top left on Figure 3) to 164,000 points (bottom right). To visualize the structure of the alternative iterations, Figure 4 includes the corresponding Brown trails of each crystal when the original pseudo-random numbers are given in terms of 1's and -1's. Notice that all trails share similar textures irrespective of the crystal's overall shape, sectored or stellar, and also independent of the presence or absence of dendritic arms. Observe that despite the use of fair coins, some trails include noticeable portions when a mapping is used more often than the other, for trails 3 and 6 exhibit sustained increases for a large portion of the iterations and trails 5, 7 and 9 contain short sharp decreases by the end. As, by construction, the crystals typically increase in size smoothly and in a manner that is roughly proportional to the number of iterations, the sustained changes in Brown trail appear to be related to specific features of the corresponding set. For instance, the increase from 45 to 75% of the iterations of trail 3 indeed reflects the emergence of the second set of (large) appendages on the arms of the bottom right pattern in Figure 3, and similarly it happens to the decrease from 85 to 100% of the iterations in trail 9 that correspond to the final tip (made of non-inclined branches) in the top right crystal in Figure 3. But when a detailed analysis is performed, however, and as hinted by the variety of patterns in Figure 3, the trails by themselves do not allow understanding the main features of a given set, for the whole history of iterations matters. This fact is vividly illustrated in Figure 5, which uses the same iterations of Figure 3 except for the middle iteration value which has been switched from 1 to -1, or vice versa. Notice how the new shapes, whose centers match those of Figure 3 but possibly at distinct scales for some of the new patterns wander also towards their center, although beautiful, are now typically incomplete pieces of snow crystals. Observe how the noted appendages on the bottom right set or the dendritic branches on the top right of Figure 3 no longer appear and how even crystals with 12 arms, as sometimes seen in nature,6 are generated. As shown by the graphs thus far and as implied by the 2M possible scenarios for M iterations for a given set-up of interpolating points, rotations, and scaling signs, usage of simple affine mappings yielding space-filling fractal wires result in a rather vast depository of 6-fold symmetric shapes that can not be studied in a systematic fashion. But although this is the case, it turns out that it is easy to find patterns inside the bell that look like "snow crystals,'' as illustrated herein. For example, Figure 6 shows that splendid crystals may be "grown'' by combining portions of the paths of iterations that gave rise to the structures in Figure 3 (in the same order), pasting together the 1's and -1's of two of them, to obtain crystals with the same number of points as those in Figure 3, such that their centers (possibly rotated by 30 degrees for aesthetic reasons) match. As recorded in Table 2, the sets in Figure 6 share either the 50 or 75% center of those in Figure 3, and result in varied geometries stemming from the corresponding tail iterations of another crystal. For instance, the left bottom set in Figure 6 is made of 109,000 dots, half of which correspond to the same set in Figure 3 (with a 30-degree rotation), and the rest of the crystal comes from the last 54,500 iterations of the top left set in Figure 3 (i.e., the one numbered 7). Similarly, the left top set in Figure 6 is made of 83,000 points, 75% of which correspond to the same Bentley's pattern in Figure 3, and the remaining 25% (20,750 dots) from the tail of the center top set in Figure 3 (i.e., the one numbered 8), and so on. Notice how these new crystals typically do not inherit the shape implied by a tail of iterations (as already alluded to in regard to Figure 5), except for the dendritic pattern in the top center (i.e., number 8) which quite accidentally preserve the tail of the bottom center crystal in Figure 3. These trends were also noticed on a complete study of all combinations of crystals in Figure 3 by couples, such that their centers are preserved at the 25, 50, 75 and 90% levels, which gave a variety of patterns that could or could not (as those in Figure 5) be classified as "ice crystals.'' As shown in Figure 6, however, it is indeed possible to find beautiful sectored and stellar crystals, whose shapes may be further grown either way using additional suitable iterations, to find yet other sectored or stellar crystals. In the same spirit of Figure 6, Figure 7 shows that other beautiful crystals may be found inside a circular bivariate bell when other set-ups of scaling signs are used, i.e., another one of the twelve cases that may be chosen out of the 24 = 16 sign combinations, for the remaining four result in symmetric patterns with rotational traits not seen in natural ice crystals.12 Observe how these mathematical designs, having by construction the same number of points as those in Figure 3, see Table 3, yield varied patterns with exquisite shapes both inside and towards their boundaries, whose dots "dance'' in and out, as in natural ice crystals,6 as if painted by an artist having six hands. Clearly, the figures shown thus far are just a very small
subset of what is surely concealed inside the circular bell while using
a given set-up of affine functions and iterations. This observation is
further illustrated in Figure 8, which shows that other
interesting sets may be found while using a 30-70% biased coin to guide
the iterations, just using pseudo-random numbers.10
Observe how these distinct sets, now more blue than green, and made of
an arbitrary number of 100,000 dots, see Table 4, furnish
us with an invitation to further explore what is found in "the plenitude
of dimension'', inside the bell.
4. ICE CRYSTALS VIA THE BINARY DIGITS OF p As random iterations are at the core of the constructions, it is natural to study the kinds of (deterministic) patterns that may be generated via the binary expansion of celebrated irrational numbers, such as p. In such a spirit, Figures 9 and 10 confirm that a wide variety of stellar and sectored "ice crystals'' may be found inside the bell, respectively, from space-filling fractal wires that pass by alternative interpolating points corresponding to diverse scaling signs and rotation angles, see Tables 5, 6, and 7, when the iterations are started at the corresponding mid-point (as all along), using chunks of 100,000 binary digits of p at a time. Notice how such crystals, now colored red and blue depending on w1 and w2, give indeed additional interesting shapes that resemble those found in nature, although the shapes of some of the crystal-tips may require additional iterations to acquire complete realism. It turns out that additional crystals may also be found via iterations of affine mappings when equations (2) and the ordering of interpolating points in x are replaced by
such that the n-th affine mapping contracts the horizontal space [x1L, xNR] (x1L = min xnL, xNR = max xnR) into end-point intervals [xnL, xnR], leading to general attractors that are either functions that have the structure of a Cantor set, when the union of the end-point intervals does not cover the domain [x1L, xNR], or not functions at all, when the aforementioned end-point intervals overlap.5 Observe in Figures 11 and 12,
and in the companion Tables 8, 9 and
10, how these cases also define beautiful stellar and
sectored "ice crystals,'' respectively, patterns made via 100,000 binary
digits of p each that have interesting dynamics
irrespective of their underlying attractors: Cantorian as in cases 2 and
5 in Table 9 or non-functional as in the remaining cases
in such a table.
5. CONCLUDING REMARKS It has been shown, via a variety of examples, that the bivariate circular bell may be constructed iterating arbitrarily two (or more) simple affine mappings, to yield 6-fold symmetric patterns that closely approximate the intricate and beautiful geometric structure seen in natural ice crystals. As it is believed it happens in nature,6 it has been illustrated that details matter quite a bit, for the presence of stellar or sectored crystals may not be discriminated from the order of iterations alone, for such define the precise growth and the ultimate shape of a crystal inside the bell. Given the hexagonal lattice structure of the ice molecule, the general connection of the Gaussian distribution with the process of diffusion, and the random addition of atoms involved via collisions,7 the results herein suggest that the iteration of affine mappings may be useful to further understand the physics of ice crystal growth, specially when subsets of iterations are identified which result in suitable shapes (i.e., with proper tips for stellar crystals) not just for a given number of iterations, but all along, as it should be possible to achieve given the success in matching Bentley's shapes. Not diminishing the value of other constructions via differential
equations and cellular automata,8 the one
given here, surely non-unique for it is just a matter of patience to find
other suitable iteration pathways that may fill a given template, may help
clarify the origins of order for these and other crystals at "the plenitude
of dimension,'' via a remarkable central limit theorem that yields a vast
array of patterns having arbitrary n-fold symmetries.12
Certainly, as Ian Stewart succinctly puts it "snowflakes are snowflake-shaped,''13
and they may also be mathematical designs concealed inside the harmonic
and ever present bell, via a exotic and lovely puzzle.
Acknowledgements This work was possible due to the gracious support of
Akin Orhum, Daniel Fessler, and Dick Odgers. The authors dedicate this
work to their daugthers Cristina and Mariana.
References
Table 6 shows interpolating points.
Table 6 shows interpolating points.
Table 9 shows end-points.
Table 9 shows end-points.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||