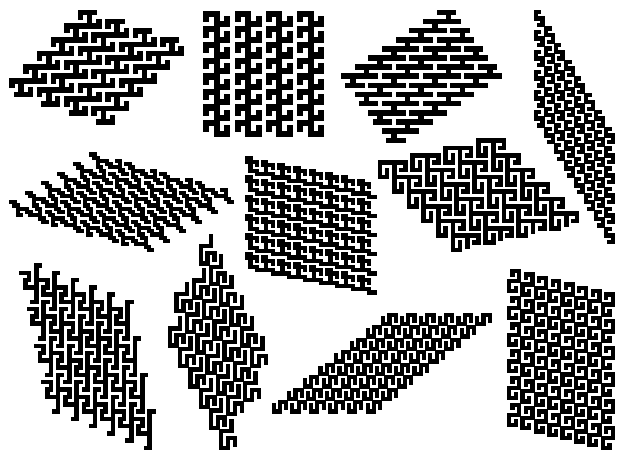|
OF ORNAMENTS Ljiljana Radovic Faculty of Mechanical Engineering
E-mail: liki@masfak.ni.ac.yu
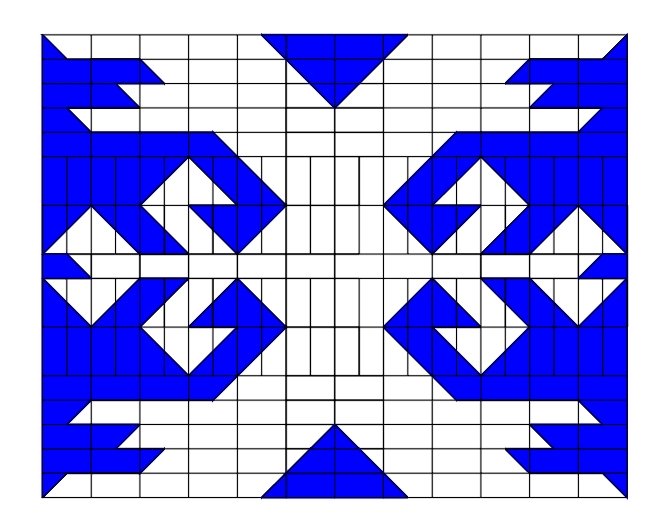
In the many cases, working with archaeological material, it is necessary to make a reconstruction of complete ornaments from their parts preserved on bone, stone, ceramics or textile. One of the possible ways is the use of symmetry (antisymmetry, colored-symmetry), where the complete ornament is extrapolated using plane symmetry groups and periodicity [1, 2]. It is interesting to notice that several antisymmetry rosettes and the most of antisymmetry friezes and plane antisymmetry ornaments can be derived in a very simple way, using just one basic element: Truchet tile (a black-white square) or a full set of tiles derived from a square by its all black-white colorings. The same holds for a remarkable collection of antisymmetric patterns presented in one Cakaudrove cloth decoration, used as a cover of the book "Symmetry of Cultures" by D.K. Washburn and D.W. Crowe [3]. This indicates that artists and artisans even in the Neolithic period, or in ethnic art, from the prehistory till our days sometimes used a very restricted set of basic elements and their recombination. This is exactly the essence of the concept of modularity [4]. Modularity in art occurs when several basic elements (modules) are combined to create a large number of different (modular) structures. In art, different modules (e.g., bricks in architecture or in ornamental brickwork) occur as the basis of modular structures. In science, modularity is represented by a search for fundamental units and basic elements (e.g., physical constants, elementary particles, prototiles for different geometric structures, etc.). In various fields of (discrete) mathematics, the search for modularity is the recognition of sets of basic elements, construction rules and the exhaustive derivation of different generated structures. In a general sense, modularity is a manifestation of the universal principle of economy in nature: the possibility for diversity and variability of structures, resulting from some (finite and very restricted) set of basic elements by their recombination. In all such cases, the most important step is the choice, by recognition or discovery, of the basic elements. This is illustrated by examples from ornamental art, where some elements originating from Paleolithic or Neolithic art are still present in ornamental art as "ornamental archetypes". One of them, discovered already in prehistory independently by different cultures distant in space and time, is the Truchet tile. Using the modularity from every set of modules by their recombination it can be obtained a large collection of different ornaments. Therefore, having a larger amount of archaeological material we may try to find the same modules occurring in different pieces and proving the modular basis of the ornaments in question. The other similar antisymmetric prototiles are obtained when some simple tile, a square, rectangle or triangle, is divided in 2 or more parts. From this division, by a systematic coloring, a full set of antisymmetry tiles is derived. If a basic tile is divided in n subregions, that complete set consists of 2n two-colored tiles (Fig. 1). That method is used by A.M. Zamorzaev, A.F. Palistrant and other authors in order to visualize multiple antisymmetry groups by their mosaics [5]. A series of interesting ornaments of that kind was found in the authors’ attempts to make a symmetry reconstruction of the patterns from the kilims (carpets) from Pirot (Serbia, Yugoslavia) [6] or much older Turkish carpets [7]. In both cases we were able to recognize a simple set of two-colored rectangular or square elements (i.e., the complete set of antisymmetric prototiles) used as the modules (Fig. 2).
Figure 1.
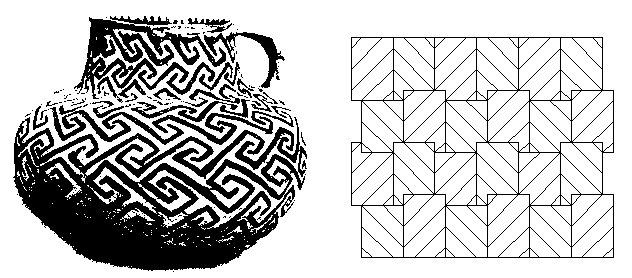
Figure 2. In those and in similar Neolithic patterns we can recognize a higher level of antisymmetry organization: instead of using a particular disjoint element arranged according to the laws of antisymmetry, here we have a complete counterchange – the perfect two-colored ornaments where the figure (black part) is congruent with the ground (white part), covering a plane without gaps or overlaps. The patterns with zoomorphic counterchanging congruent tiles were created by M.C. Escher, but a large number of such geometric ornaments can be found in the Neolithic ornamental art. In that sense, the patterns and the details from the kilims from Pirot or Turkish carpets could be considered as a treasure preserving some much older knowledge, originating even from prehistoric times. For Neolithic ceramic ornaments, this kind of a perfect counterchange is not an exception, but almost a rule. This can be shown by analyzing black-white patterns from the Neolithic of Hungary, Romania, Greece, and Yugoslavia. According to Nandor Kalicz [8], their common origin could be the Neolithic textiles, i.e., matting, which them the ornaments have been copied to the other stronger media (ceramic) (Fig. 3).
Figure 3. The other prototile based on the antisymmetry and used abundantly in ornamental art, even from the time of the Paleolithic, was a square with a set of diagonal bands. Decomposing such a square into two squares (a "positive" and "negative") and arranging them in patterns by using very simple repetition or alternation rules (left, right, left, right, etc.), an infinite series of patterns can be obtained. Those patterns, known as "key-patterns", are common for different cultures (Paleolithic, Neolithic, Chinese, Celtic) and were independently discovered by them. The oldest examples of key-patterns are ornaments from Mezin (Ukraine, about 23 000 B.C.) (Fig. 4) [9]. After that, their appearance in prehistoric ornamental art can be traced in archeological findings from Moldavia, Romania, Hungary, Yugoslavia, and Greece, and all of them can be derived as modular structures (Fig. 5). It is interesting that almost identical key-patterns can be found in widely separate parts of the world (e.g., in Hungary and in Fiji islands, as Lapita patterns (Fig. 6), both in the ceramics from the Neolithic period, in Celtic art [10], as well as in Anasazi pottery (Fig. 7)). This could be considered as evidence that different cultures discovered the same basic elements and created even the similar or same ornaments by using modularity. Because of their similarity with Neolithic ornaments from different parts of Europe, we will try to prove their same technological origin: production of textile designs that are later transferred to ceramics.
Figure 4.
Figure 5.
Figure 6.
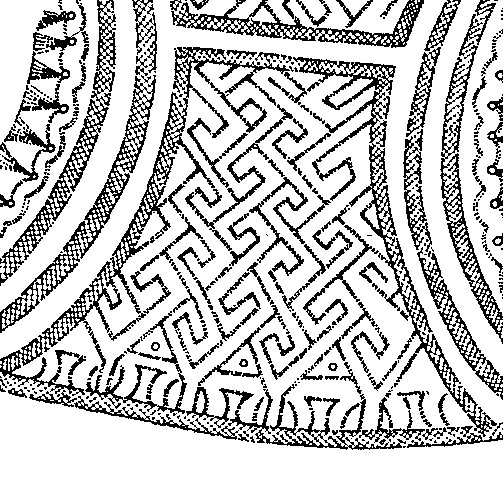
Figure 7. The same basic elements, "positive" and "negative" square with diagonals, is also preserved in another very ancient kind of art: in the art of mazes. That art, known from Greek mazes (labyrinth from Knossos)(Fig. 8), Roman mazes, or Celtic mazes [11, 12], probably comes from much older, Neolithic or even Paleolithic origin.
Figure 8.
References: [1] Jablan S., Symmetry, Ornament and Modularity, World Scientific, Singapore, 2002. [2] Radovic Lj., Antisimetrija i visestruka antisimetrija, M.A. Dissertation, Univerzitet u Nisu, 2000. [3] Washburn D.K., Crowe D.W., Symmetries of Culture, Theory and Practice of Plane Pattern Analysis, University of Washington Press, Washington, 1988. [4] Jablan S., Modularity in Art, http://members.tripod.com/modularity/ [5] Zamorzaev A.M., Teoriya prostoi i kratnoi antisimmetrii, Shtiintsa, Kishinev, 1976. [6] Zivkovic M., Album pirotskih cilimova, Tesen (Austrija), 1902. [7] Erbek G., Kilim: Catalogue No. 1, Selçuk A.S., Istambul, 1990. [8] Kalicz N., Die Gotter aus Ton, Corvina Verlag, Budapest, 1989. [9] Gimbutas M., The Language of the Goddess, Harper & Row, San Francisco, 1989. [10] Bain G., Celtic Art - the Methods of Construction, Dover, New York, 1973. [11] Mathews W.H., Mazes & Labyrinths: their History and Development, Dover, New York, 1970. [12] Meehan A., Maze Patterns,
Thames and Hudson, New York, 1993.
|