1. Glide Reflection.

First let's have a closer look at Glide Reflection. Maybe one of the most well known examples is M.C. Escher's Horseman (Figure 1) [1]. The shapes of the light and dark horseman are the same apart from the operation of reflection. If you want to place a tile of a light horseman on a tile of a dark horseman, you can't do that with just reflection, rotation or translation. You have to use both translation and reflection. These two transformations have to be used together (Figure 2, 3, 4).
 

This gave me the idea to explore other combinations of transformations which could be used together.
 
 

I examined the following combinations: a) rotation + translation which I will call Swing Translation, b) rotation + rotation (different axis) this is called Swing Rotation and c) rotation + scaling, Swing Scaling.

The purpose of this examiation was to see whether it could lead to designs or objects in which a combined transformation is a generating element.

A first remark maybe that we know representations of all three combinations: the helix, the moebius strip and the spiral. In this article I will focus on Swing Translation.
 
 

3.1 Basic Principle. Combining the two transformations rotation and transformation can be done in a few different ways. We will start with the restriction that the direction of translation has to be along the rotational axis. Moving a point continuously this way in 3-dimensional space will result in a helix. But as with the tilings we will first use this transformation with discontinuous steps to build 3D objects.

As an example we start with a basic shape which consists of two connected tetrahedra (Figure 5 left). Like in tilings we add a next element to the first one. When we combine them face to face as in Figure 5 (middle), you will see that the transformation which is needed to go from the first double-tetrahedron to the second is a combination of a rotation and a translation. Going on with this process will result in the well known tetrahelix (Figure 5 right) [2].
 

3.2 Variations. Now that we have seen the principle we can make variations. Instead of starting with a basic element of 2 tetrahedra we can take one which consists of 3 (Figure 6) or 4 tetrahedra (Figure 7). The result is again a tetrahelix but very different from the first one.
 

3.3 Relation between Glide Reflection and Swing Translation. Let's go back to the Escher tiling with the Glide Reflection for a while. There is an alternative way to make the transformation from the light horseman to the dark one. I will illustrate this using another tiling of M.C. Escher, regular tiling No. 17 [1].
 

Another way to make the transformation from one white bird to the white bird which is in the row above is the use of Swing Translation (Figure 9, 10).
 

Applying Swing Translation in a continuous way to the white bird tile will result in the weird spiral shape of Figure 10. In fact the 2D tiling is then an intersection with a plane and these spiral shapes. Note that this kind of helix can be made with the bird looking outwards and with the bird looking inwards. And the helical shapes can be entwined!
 

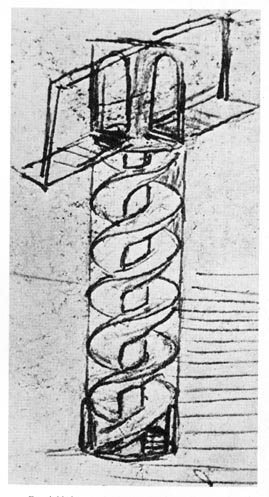
3.4 Spiral Dissection. The object of Figure 10 is in fact one part of a dissection of a cylinder into two parts. This structure could also be recognized in the tetrahelix of Figure 5. And also Leonardo da Vinci made use of it in his drawing for the double spiral staircase (Figure 11) [3].

In these examples the spiral cut is applied to cylindrical shapes. The parts are still close to the normal spiral shape. When we apply the spiral cut to a cube the shape of parts becomes more interesting. So we can divide a cube into two equal spiral shapes that can be twisted in and out each other (Fig. 12). And even a spiral dissection of a sphere can be made (Fig 13.).
 

3.5 Other Examples. Let us consider a few examples based on polyhedra. The first is an object made with cubes. I started with a set of two linked cubes as in Figure 14.
 

In both cubes (Fig. 14) a line is added to indicate where a next set of cubes is to be placed. To go from one marked edge to the other marked edge you need the combined tranformation of translation and rotation. And after adding more sets of linked cubes the result is an object that can be seen as a combination of two strings of cubes, spiralling around each other (Fig 15).

In the next example the dodecahedron is the basic element to which the Swing Translation was applied. In the final object only a part of the spiralling edges are left to create an open structure.
 

The object in Figure 17 may look like a set of linked cubes. But when you take a closer look you may see that it is a string of linked squares. The ground plan for the object is the 9,2 star polygon as can be seen in Figure 18. When spiralling around the squares get entwined and we get the nice suggestion of the linked cubes.
 

[1] Doris Schattschneider, Visions of Symmetry - M.C. Escher, W.H. Freeman and Company, New York. 1990.

[2] Pugh, Polyhedra - A Visual Approach, Dale Seymour Publications, Palo Alto. 1976, 1990.

[3] Carlo Pedretti, Leonardo Architect, Rizzoli International Publications, New York. 1985.