|
Modularity in Medieval Persian Mosaics: Textual, Empirical, Analytical, and Theoretical Considerations Reza Sarhangi Mathematics Department Towson University Towson, MD 21252, USA Slavik Jablan and Radmila Sazdanovic The Mathematical Institute Kneza Mihaila 35, 11001 Belgrade, Serbia & Montenegro Abstract
1. Introduction In Mathematics and Arts: Connections between Theory and Practice in the Medieval Islamic World [1], we read: "Intriguing patterns ornamenting architectural monuments and other objects of art bear witness to the predominance of geometry in Islamic art. Traditionally, the artisans who produced them were believed to be experts in geometry. Recent studies, however, have shown that mathematicians who taught practical geometry to artisans played a decisive role in the creation of those patterns and perhaps in designing the buildings themselves." The purpose of this article is to not only emphasize the expertise of artisans as well as the direct involvement of mathematicians in Persian art of the medieval time, but also to suggest the use of modularity in creations of some classes of patterns. Through comparison of extant designs and models we present the possibility of techniques of trial and error used by artisans to create fascinating designs based on sets of tiles we called "Kufi modules." In the present article, for our discussions, we mainly rely on two resources: a treatise written by Buzjani in the 10th century, On Those Parts of Geometry Needed by Craftsmen [2], and a modern five volume book of design construction illustrations and related images entitled Construction and Execution of Design in Persian Mosaics [3]. The treatise by Buzjani was originally written in Arabic, the academic language of the Islamic world of the time, and was translated to the Persian language of its time in two different periods: 10th and 15th centuries. There are only a few known original translations of this book in the world; two of them are kept in two libraries in Iran, Tehran University Library and Astan Ghods Razavi Library, and another in the National library in Paris. The book Applied Geometry, which includes a contemporary Persian language translation of Buzjani’s treatise appeared first in 1990 and then was republished with some corrections in 1997 [2]. The book also includes another treatise of later centuries: Interlocks of Similar or Corresponding Figures. Even though the book introduces a 15th century Persian mathematician as the author of this treatise, there are documents that suggest the possibility of a much earlier time writer, around the 13th century, for this work [1]. Perhaps the most comprehensive and elegant recent book about Persian mosaics that includes geometric constructions of designs presented along with colorful images of their executions performed on different mediums on the wall, floor, interior and exterior of domes, doors and windows, and many more, is Construction and Execution of Design in Persian Mosaics written by Maher AnNaghsh [3]. The author, who is a professional artisan, inherited his profession from his ancestors of several centuries, has the most access to original artisans’ repertories of the past. The ornamental qualities of these geometric constructions and their executions provide a joyful journey to the past for readers. In the next section we introduce Buzjani by illustrating his "cut and
assemble" method of squares. In section 3 we present
what we propose as a modular art, based on the color contrast of sets of
cut-tiles. Section 4 proposes the possibility of "gaps"
and "overlaps" as two ideas for creating other ornamental designs based
on modularity. In section 5 we introduce Kufi modules
and show how this set has the capacity of generating a large number of
traditional ornamental and calligraphic designs.
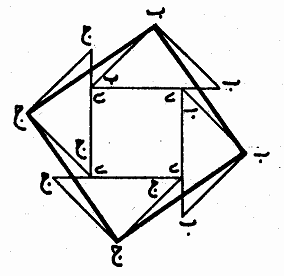
2. Abul Wafa, Mohandes Abul Wafa al-Buzjani was born in Buzjan, near Nishabur, a city in Khorasan, Iran, in 940 A.D. He learned mathematics from his uncles and later on moved to Baghdad when he was in his twenties. He flourished there as a great mathematician and astronomer. He was given the title Mohandes by the mathematicians, scientists, and artisans of his time, which meant "the most skillful and knowledgeable professional geometer." He died in 997/998 A.D. Buzjani’s important contributions include geometry and trigonometry. He was the first to show the generality of the sine theorem relative to spherical triangles and developed a new method of constructing sine tables. He introduced the secant and cosecant for the first time, knew the relations between the trigonometric lines, which are now used to define them, and undertook extensive studies on conics. In geometry he solved problems about compass and straightedge constructions in plane and in sphere. Buzjani wrote in On Those Parts of Geometry Needed by Craftsmen that he participated in meetings between artisans and mathematicians. "At some sessions, mathematicians gave instructions on certain principles and practices of geometry. At others, they worked on geometric constructions of two- or three- dimensional ornamental patterns or gave advice on the application of geometry to architectural construction [1]." Such gatherings were usual practice in the Islamic world in medieval times. "Ghiyath al-Din Jamshid al-Kashi solved a problem about a triangular leveling instrument at the construction site of the astronomical observatory in Samarkand during a meeting of artisans, mathematicians, and other dignitaries [1]." Therefore, it will not be far from the truth if we claim that some of the spatial properties and aesthetic elements in the structures of the Islamic art and architecture come from the direct involvements of mathematicians. In his treatise, in a chapter titled "On Dividing and Assembling Squares," Buzjani presents the two different attitudes of mathematicians and artisans toward geometry: A number of geometers and artisans have made error in the matter of these squares and their assembling. The geometers made error because they don’t have practice in applied constructing, and the artisans because they lack knowledge of reasoning and proof. He continues: I was present at a meeting in which a number of geometers and artisans participated. They were asked about the construction of a square from three squares. Geometers easily constructed a line such that the square of it is equal to the three squares but none of the artisans was satisfied. They wanted to divide those squares into pieces from which one square can be assembled. Buzjani describes what he means by the mathematicians’ approach for
solving this problem. In the following figure
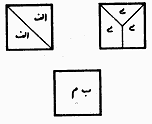
Figure 1: Consecutive constructions of Then artisans presented several methods of cutting and assembling of these three squares. Some of these methods based on mathematical proofs turned out to be correct. Others were incorrect, even though they seemed correct at first glance. Buzjani illustrates two of these incorrect cutting-and-pasting constructions. We show one of them here: Some of the artisans locate one of these squares in the middle and divide the next one on its diagonal and divide the third square into one isosceles right triangle and two congruent trapezoids and assemble together as it seen in the figure.
Figure 2: An incorrect construction of a square
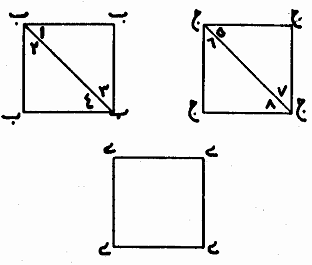
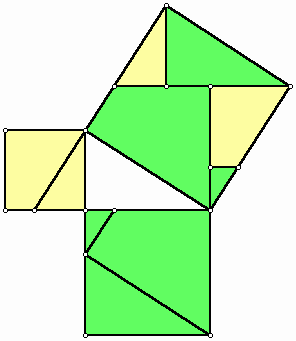
from three unit squares. For a layperson not familiar with the science of geometry, this solution seems correct. However, it can be shown that this is not the case. It is true that the resulting shape has four right angles. It is also true that each side of the larger shape seems to be one unit plus one half of the diagonal of the unit square. However, this construction does not result in a square because the diagonal of the unit square (which is the hypotenuse of the assembled larger triangle) is an irrational number but the measure of the line segment that this hypotenuse is located on in the larger shape is one and half a unit, which is a rational number. Buzjani includes more information and simple approximations to reinforce his point that the construction is not correct. However, his way of using an argument based on the idea of rational and irrational numbers is undoubtedly elegant. He then after presenting another incorrect artisans’ way of cutting and pasting gives his solution, which is mathematically correct. At the practical level it can be performed in any medium by artisans. But on the division of the squares based on reasoning we divide two squares along their diagonals. We locate each of these four triangles on one side of the third square such a way that one vertex of the acute angle of the triangle to be located on a vertex of the square. Then by means of line segments we join the vertices of the right angles of four triangles. From each larger triangle a smaller triangle will be cut using these line segments. We put each of these triangles in the congruent empty space next to it to complete the square.
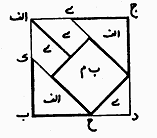
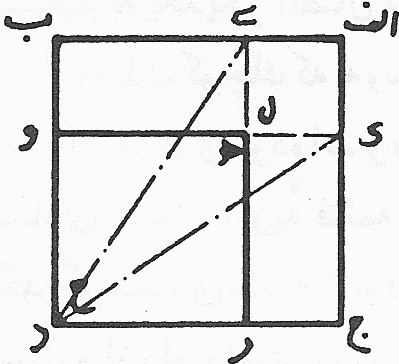
Figure 3: The correct construction of a square from three unit squares. Another interesting problem that Buzjani presents in his book is the composition of a single square from a finite number of different sizes of squares. For this, he solves the problem for two squares first and then comments that with the same method we are able to solve the problem for any number of squares.
Figure 4: Generating a square from two different sizes squares. The proposed solution for two squares is again based on cutting and pasting squares and therefore is acceptable by artisans. His solution is elegant: We first put the small square (a) on the top of the larger square (b) and then draw necessary line segments presented in (d) and (e) and finally cut the solid lines and paste them to obtain the resulting square.
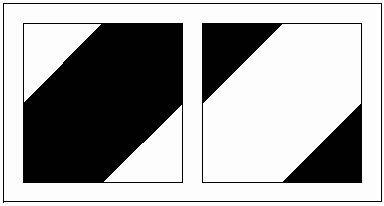
Figure 5: The details of generating a square from two different squares. For a person familiar with elementary mathematics what Buzjani is doing in this problem can be justified as follows: Let a be the size of a side of small square and b the size of a side of the large square. Then the sum of the areas of these two squares will be a2 + b2. Now the cuts will create four right triangles with sides a and b (and hypotenuse Ö (a2 + b2)), and a square with side equal to b -a. The way that we arrange these four right triangles and the little square is in fact the visualization of the following equation: 3. Modularity Art: Elementary Trial and Error, Sophisticated Symmetry It may seem that some of the cutting and pasting activities presented in On Those Parts of Geometry Needed by Craftsmen by Buzjani such as mentioned above are simply mathematical challenges and lack practical value. However, if we study ornamental designs in Persian arts and architecture closely we notice the use of modular designs based on assembled cut-tiles. "Recently discovered authentic plans of buildings and architectural decorations show that their designs were based on square-grid layouts or radial organization of squares and rhombi. The 15th-century mathematician Ghiyth al-Din Jamshid al-Kashi noted that muqarnas designs were generated from a unit square which he specifically referred to as "module" (migyas)."[1] So far we have seen that by using these modules one can approach ornamental qualities of patterns created by ingenious processes executed by either highly skilled artisans or mathematicians. What we wish to propose is controversial: There is the possibility that not very skilled artisans, who had no access to geometers, by the use of elementary cut-and-paste processes, based on trial and error, could create complex designs that require sophisticated geometric explanations—processes that remind us of modern fractal geometry: simple input with complicated results. The widespread approach for constructing and arranging pattern designs in ceramic mosaic during the 10th and 11th centuries was the use of squares. The economy of energy and space for molding, casting, painting, and baking tiles forced artisans to use single-colored square tiles. The four colors available were light blue, navy blue, brown and black. The color scheme improved rapidly by increasing the number of colors made through different combinations of metals [4]. It is natural to assume that a practical way of achieving new patterns from these squares for some artisans would be to cut them in different formats and assemble them such a way that different colors replace one other in new arrangements. In this way the artisans could rely on the color contrast of cut-tiles to emphasize designs, rather than use a compass and straightedge. An elementary example would be to consider congruent squares in two colors of black and white. If we cut an isosceles right triangle with sides equal to one half of the side of these squares in one color and exchange it with the other triangle with opposite color, we have two two-color "modules" where one is the negative of the other. Now if we also include the two original single-color square designs, then we have four modules to work with to create patterns.
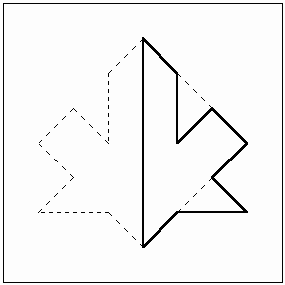
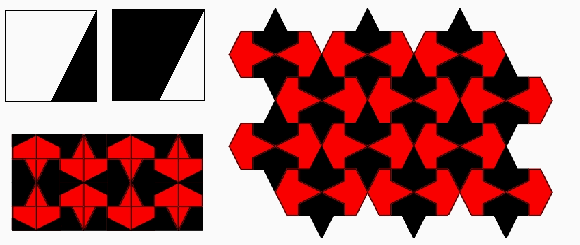
Figure 6: Four modules created based on two different colors of congruent squares. One interesting Islamic pattern is the "maple leaf". Polya illustrated the 17 wallpaper patterns in his article "Über die Analogie der Kristallsymmetrie in der Ebene" published in Zeitschrift für Kristallographie in 1924. He illustrated a maple leaf pattern and identified it as D°4. The basic shape to construct this pattern, based on Heech’s classification of the asymmetric tiles [5] that can fill the plane in an isohedral manner, is an isosceles right triangle. The isometries employed are then a quarter rotation of one side to another and then reflection of the shape under the hypotenuse. The mathematical notation for this pattern is P4m. It belongs to the square lattice of wallpaper patterns and its highest order of rotation is 4. It can be generated by 1/8 of its square unit. If we consider this design as a two-color pattern then its crystallographic group classification will be p4’g’m (2-fold rotational symmetry, vertical and horizontal reflective symmetries).
Figure 7: A "maple leaf" motif.
Figure 8: Traditional construction of the "maple leaf" pattern. Figure 8 presents a traditional means of constructing the maple leaf pattern using compass and straightedge. In comparison we wish to present the modularity method and introduce the simplest possible set of modules using two single-color square tiles cut diagonally to generate the "maple leaf" pattern. If we cut a black and a white tile from their diagonals and exchange one of the generated triangles from each then we have a set of three modules of black, white, and half black-half white tile. In any other case by a diagonally shaped cut we create four modules as illustrated in Figure 6. Truchet’s 1704 paper laid down a mathematical framework for studying permutations based on these tiles [6].Now by using 14 white, 14 black, and 8 black-white tiles we create a 36-tile grid, which is a base for construction of the maple leaf tessellation (Figure 9).
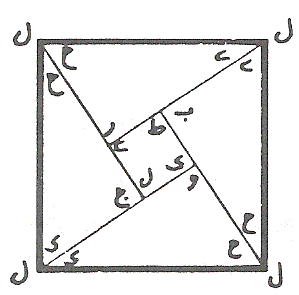
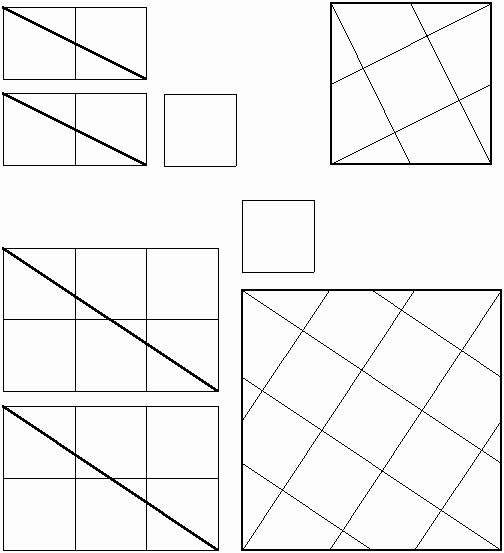
Figure 9: A set of three modules, the generated base design, and the final result for the "maple leaf" tessellation. Another interesting problem that Buzjani solved in assembling of squares is if we have (m2 + n2) squares, where m, nÎ Z+,m ³n, (the sum of two perfect square numbers) such as 5 (22 + 12) or 13 (32 + 22), then we can make two congruent rectangles, each of whose length is equal to m and their width is equal to n. Therefore, we use 2mn of our squares in this way. This is possible because of the simple fact that m2 + n2 ³2mn. But then, the unused squares make a perfect square: (m -n) 2. Now if we cut these two rectangles diagonally and arrange the pieces around the square with side m -n we find our desired square. In fact Buzjani mentions that the measure of the diagonals of the two rectangles is equal to the side of desired square (Öm2 + n2) and this is a hint for how to arrange the pieces around the square with side m -n. Figure 10 presents two examples of 5 and 13 squares, respectively.
Figure 10: Cutting and assembling a square from five square
units;
We should note that the "sum of two perfect square" problem, is in fact, a special case for the general case of "two different squares" problem, presented in Figure 4. Nevertheless the cut for the above two examples can provide us, or an artisan with a set of modules for exploring new patterns. The following figure presents a pattern, called "hat," which can be generated by only two opposite modules (without the use of original single color tiles) using the cuts from the above "5 squares" problem.
Figure 11: Modules based on the "5 squares" problem, and its generated "hat" tessellation. Figure 12 illustrates steps taken by a geometer or a highly skilled artisan to compose the "hat" grid using compass and straightedge. You may find more design constructions in [7].
Figure 12: Polygon construction approach for generating the grid for the "hat" tiling. The following tiling is generated from a set of modules that are cons-tructed from cutting and assembling thirteen squares as illustrated in Figure 10.
Figure 13: A tiling created by trial and error
from a set of modules resulting from cuts on thirteen squares.
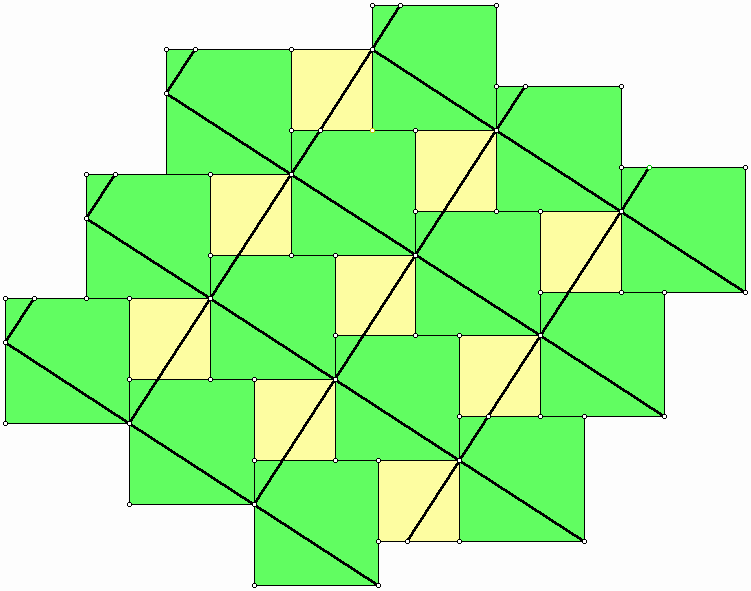
4. Gaps and Overlaps for Creating Ornamental Modules The treatise Interlocks of Similar or Corresponding Figures presents various sub-grids of ornamental geometry, which were compiled based on a series of meetings between geometers and artisans. Figure 14a shows a square polygonal sub-grid from this treatise. The artisan uses this sub-grid (and its reflection on its sides) as a motif to cover a surface. Figures 14b-c show two different ways that an artisan may use copies of this tile for tiling of a wall or a floor. The first tiling uses the copies of the original tile and its mirror image to cover a surface without any gaps (a square tessellation). However, the second tiling, that only uses the original motif, admits square-shape gaps that can be filled out by smaller squares. An immediate and obvious conclusion is that artisans of medieval Persia who had access to actual tiles tried all these possibilities for ornamental tilings and applied them in their works.
(a)
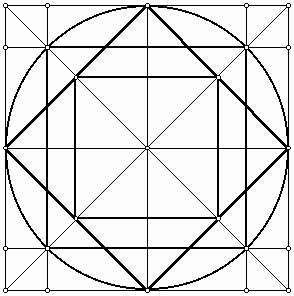
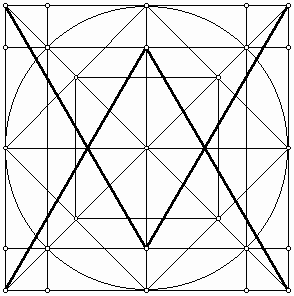
(b) (c) Figure 14: (a) Polygonal grid, (b) Tiling without gap, (c) Tiling with gap. In fact, tilings of two different size squares are not unusual in Islamic art. A proof of the Pythagorean theorem, attributed to Annairizi of Arabia (circa 900), is based on the tilling of two squares of different sizes (Figure 15). The bold overlay of larger squares presents copies of a square whose area is equal to the sum of the areas of the two square bases of the tiling. This proof is based on the cutting and assembling method [8].
Figure 15: Proof of the Pythagorean theorem by Annairizi. Unlike "gapping," when we work with actual tiles, we cannot produce "overlapping" during execution of an ornamental design on the wall. However, one step earlier, before the artisan works with actual tile, he needs to transfer the grid from his scrolls to the wall. In this step he can simply overlay several grids to produce a more detailed and attractive tiling—a perfect "overlapping." The artisans of medieval Persia were fascinated to incorporate multiple-level designs into their ornaments. One to mention among various methods was to use a smaller scale of the primary grid as an overlay in a way that vertices of the two grids coincide. "An example of an Islamic self-similar design is probably compiled in the late 15th or 16th century somewhere in western or central Iran. Pattern 28 in the Topkapi scroll is a 5-fold self-similar design that also depicts the underlying polygonal sub-grid used in the creation of the secondary design. The fact that artists and designers limited themselves to only a single iteration of self-similarity is due to the constraints of the materials than any lack of creative imagination or geometric ingenuity. [9]" The following figure presents the "maple leaf" tiling by means of a totally new construction. Here we have employed a different set of modules. Unlike the previous approach (Figure 9), we cannot create the design without using gaps and overlaps. It seems that these modules provide more capacity for creating new designs if we use proper gaps and overlaps. A person may discover this or similar tiling motif faster than using, for example, the modules that we introduced in Figure 10.
Figure 16: A new approach for creating the "maple leaf" tiling
using a set of Kufi modules.
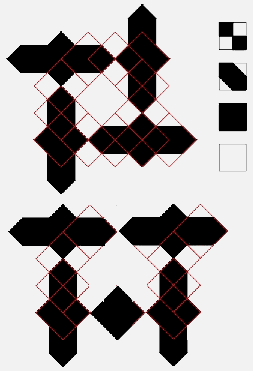
5. Kufi Modules The modules that we introduced in Figure 16 are produced from a simple procedure of two equal cuts in two opposite color tiles and the exchange of opposite color triangles. We will use these modules not only to regenerate some original Persian ornamental designs, but also to render angular and geometric Kufic calligraphy of this area. Because of the relationship to Kufic calligraphy, we have chosen to call these Kufic modules.
Figure 18: A Kufi module and its
tiling in Goharshad Mosque, Mashad, Iran.
Figure 19: Kufi module structure and a related tiling in Mazar Sharif, Afghanestan.
Figure 20: Calligraphic design
using Kufi modules and a related tiling in the mausoleum of Shahzadeh Hossein,
Ghazvin, Iran.
Figure 21: Design using a combination
of overlapping Kufi modules and checkerboard tile,
Figure 22: Design based on Kufi modules and checkerboard tile, and a similar tiling in the Ali Mosque in Esfahan, Iran. Using Kufi modules, appropriate gaps or overlaps, and appropriate use
of other tiles, we are able to generate the basic ornamental pattern for
a large class of tiling designs as we can observe in Figures
18-22. All the original patterns in these figures are from [3].
6. Conclusion The art of Medieval Persian artists and artisans demonstrates the complex
overlay of geometric patterns, floral designs, and calligraphy. They achieved
this level of sophistication by collaboration with mathematicians of their
time and by improvement of their skill levels in geometric constructions.
The most ubiquitous method in creation of the ornamental patterns for the
artisans was by means of polygonal constructions. Some cut-tile patterns
suggest a modular approach, which is based on color contrast and repetition
by trial and error methods.
References [1] A. Özdural, Mathematics and Arts: Connections between Theory and Practice in the Medieval Islamic World, Historia Mathematica 27, Academic Press, 2000, pp. 171-301. [2] S. A. Jazbi (translator and editor), Applied Geometry, Soroush Press, ISBN 964 435 201 7, Tehran 1997. [3] M. Maher AnNaghsh, Design and Execution in Persian Ceramics, Reza Abbasi Museum Press, Tehran, 1984. [4] R. Sarhangi, Persian Arts: A Brief Study, Visual Mathematics, http://members.tripod.com/vismath/pap.htm, Vol. 2, No. 1, January 2000. [5] B. D. Martin, R. Sarhangi, Symmetry, Chemistry, and Escher’s Tiles, 1998 Bridges Proceedings, Gilliland Printing, Kansas, 1998. [6] D. E. Smith, The tiling Patterns of Sebastien Truchet and the Topology of Structural Hierarchy, Leonardo 20, 4, 1987, pp. 373-385. [7] B. L. Bodner, Constructing and Classifying Designs of al-Andalus, ISAMA/BRIDGES Conference Proceedings, University of Granada, Spain, 2003, pp. 61-68. [8] R. B. Nelson, Paintings, Plane Tilings, and Proofs, Math Horizons, MAA, Nov. 2003, pp. 5-8. [9] J. Bonner, Three Traditions of
Self-Similarity in Fourteenth and Fifteenth Century Islamic Geometric Ornament,
ISAMA/BRIDGES Conference Proceedings, University of Granada, Spain, 2003,
pp. 1-12.
|