Most straight lines in Hyperbolic Geometry appear curved to us, according to our experience built Euclidean Geometry. If you could somehow be transported inside a world of Hyperbolic Geometry, then all of the "straight lines" shown in this simulation would appear perfectly straight to your vision
Moreover, each model has the property of preserving angles from the Lobachevskian plane to the model, but only Poincare models are conformal representations of angles with respect to their Euclidean measures with the angle between two arcs of circles understood in the usual way.
One of the most
interesting things about hyperbolic geometry is how so many properties
differ from Euclidean geometry. One of the striking differences is that
the sum angles in a triangle measure less than 180°.
The defect of a triangle is defined as:
δ(Δ)=π-α-β-γ
where α,β,γ are
angles of the triangle. Similar proposition applies to all polygons. A
way to see the measure of the defect is by movements in Lobachevskian
plane along the edges of a given polygon.
When we construct
Hyperbolic triangles, and measure the defect of each, we find that
for small triangles the defect is small (the angle sum is almost 180°)
and vice versa.
In fact, as the perimeter of triangle approaches
zero,the angle sum approaches 180°. This is consistent with the idea
that a relatively small piece of Hyperbolic Space looks, and behaves very
much like Euclidean Space. Our choice
was to present this feature on regular octagon:
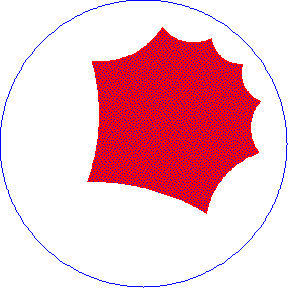 |
 |
|
Poincare Disk
|
Poincare Halfplane
|
and to You we leave the question:
IS THE WORLD THAT WE ARE LIVING IN JUST A SMALL PIECE OF HYPERBOLIC SPACE?
