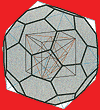
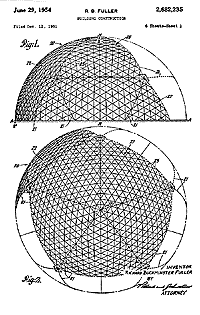
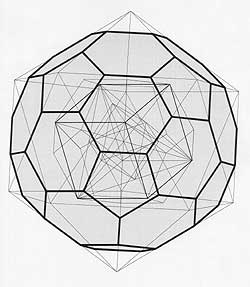
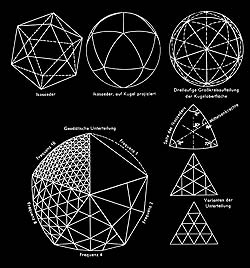
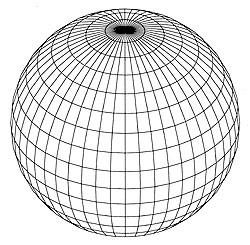
Fullers constructions are networks of triangles spread over a sphere, produced by great circles crossing over it. He calls these structures "geodesics". Fuller considered the geodesic dome as triangular faces projected onto a sphere by great circles running in three directions.

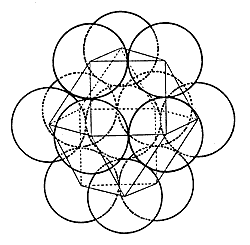
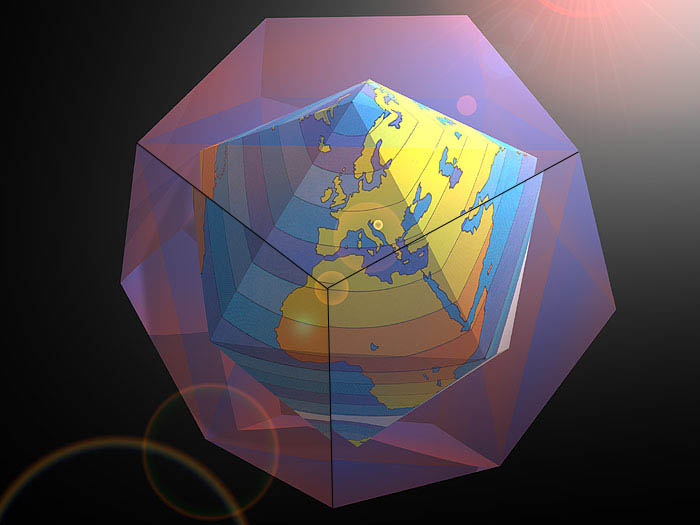
From another viewpoint, these are projections of different polyhedrons from a centre point onto a surrounding sphere, whereby the vertices of the polyhedrons actually lie on the spherical surface.

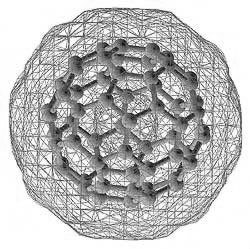
Fuller's Patent of 1954 presents a fundamental figure, a projection of the (truncated) icosahedron onto the circumscribing sphere. We thus always have 12 pentagons on the corners of the icosahedron, the remaining projected triangles can be subdivided into triangles, hexagons or rhombuses; the possible steps in this subdivision process are called "frequencies" by Fuller.

In order to generate geodesic domes, one can project any desirable Platonic or Archimedean polyhedron onto a sphere; these all are contained in the Metaeder.

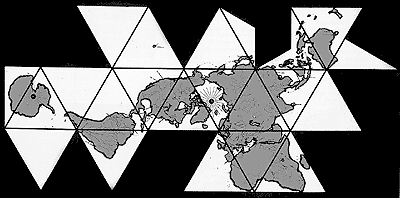
Fuller developed his cartographic "Dymaxion Map", which - contrary to the standard Mercator projection - shows considerably fewer distorsions when projecting a sphere onto a flat surface. It represents a projection of the globe onto the circumscribed icosahedron or other polyhedrons.

Snelson, Fuller and his adherents found the principle of "tensegrity", static constructions using discontinuous compression members and continuous tension members, building a series of figurations and domes on the basis of the polyhedrons.

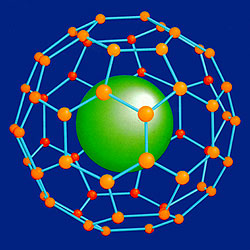
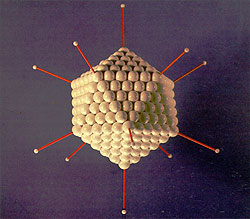
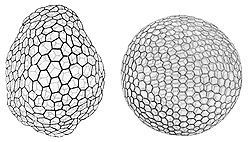
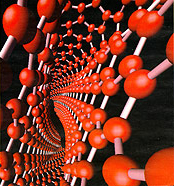
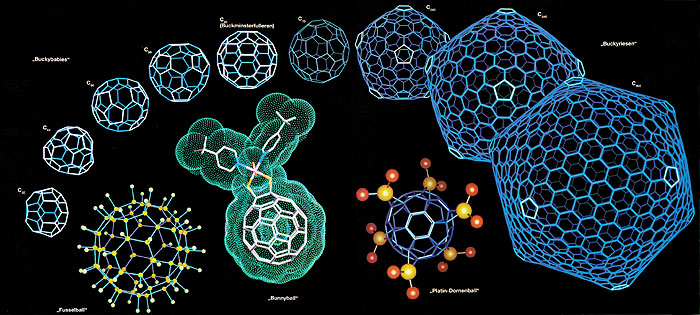
In 1985, chemists discovered a new modification of the carbon molecule called the fullerene, in addition to the diamond and graphite forms of carbon already known before. In its configuration, the diamond is an arrangement of tetrahedral umbles, and graphite consists of hexagonal rings; that of the C60 Buckminster fullerene, i.e. the fullerene having the greatest symmetry, unites 60 carbon atoms to to form a nearly spherical molecule in the form of a truncated icosahedron (one of the Archimedean solids) or, that of a football.

In 1996, Kroto, Curl and Smalley received the Nobel prize and called the new carbon modifications "fullerenes".

"Researchers have been studying the class of molecules called fullerenes for over 15 years. Now, scientists at the University of Freiburg (in Germany) have succeeded in producing the smallest possible fullerene. It consists of only twenty carbon atoms arranged in the order of twelve pentagons and thus forming the geometric body of a dodecahedron." (Frankfurter Allgemeine Zeitung)