Analogies from 2D to 3D
Exercises in Disciplined Creativity
Computer Science Division, EECS Department
University of California, Berkeley, CA 94720
E-mail: sequin@cs.berkeley.edu
Abstract
Human creativity
reliesto a large part on our ability to recognize and match patterns, to
transposethese patterns into different domains, and to find analogies in
new domainsto known facts in old domains. In the realm of geometrical proofs
and geometricalart, such analogies can carry concepts and methods from spaces
that areeasy to deal with, e.g. drawings in a 2-dimensional plane, into higher
dimensions where model making and visualization are much harder to carryout.
Students in a graduate course on geometric modeling are challengedwith open-ended
design exercises that introduce them to this analogicalreasoning and, hopefully,
enhance their creative thinking abilities. Examplesinclude: constructing
a Hilbert curve in 3D-space, finding an analogousconstellation to the Borromean
rings with four or more loops, or developing3D shapes that capture the essence
of the 2D Yin-Yang figure or of a logarithmicspiral. The proffered solutions
lead to interesting discussions of fundamentalissues concerning acceptable
analogies, the role of symmetry, degrees offreedom, and evaluation criteria
to compare the relative merits of thedifferent proposals. In many cases,
the solutions can also be developedinto attractive geometrical sculptures.
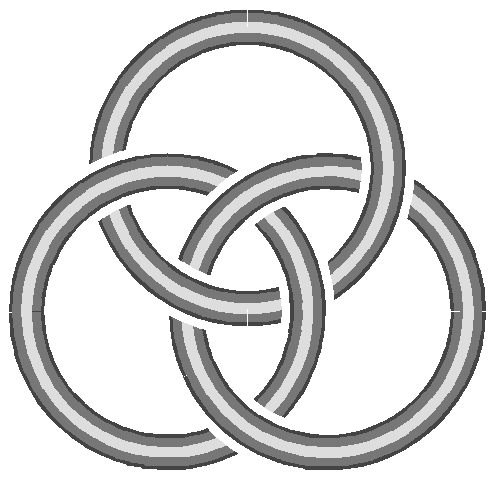

Introduction
Where
does creativitycome from? What is "good design"? How do we know that we have
a "solution"to a design problem? These are some questions behind the design
exercisesthat I will discuss in this paper.
The human mind
is good at discoveringpatterns. One might argue that human intelligence and
creativity reliesto a large extent on our ability to recognize patterns and
match them withpreviously stored patterns. We easily see animal shapes and
faces in clouds,or goblins and ghosts in tree trunks at night in the forest.
We are intriguedby star constellations if they approximate regular triangles
or quadrilaterals,or if they lie on a roughly circular arc. We also recognize
and enjoy theregularity in tiling patterns. Often we try to explain the patterns
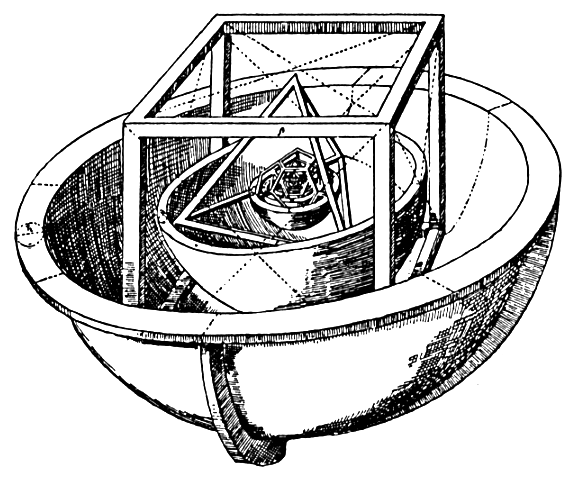
inone domain with patterns from another domain. For example, Kepler tried
to explain the relative sizes of the planetary orbits with the suitablynested
circumspheres of the Platonic solids (
Fig.2), and there were attempts to draw the periodic table onto simple
geometricalobjects such as cylinders. Often we use analogies to try to explain
a newand unfamiliar domain with a model from a well-understood and intuitively
plausible domain; as an example, the model of water flowing over a damof
adjustable height has been used to explain the operation of an MOS fieldeffect
transistor [
8].
I believe that
one's creativityand imagination can be improved by training one's ability
to find suchanalogies. This is why I include such exercises in almost every
courseI teach at U.C. Berkeley. I try to improve the students' design skills
by raising to a conscious level sequences of thoughts and associationsthat
appear in the search for a solution. We ponder questions such as:What is
going on in the design process? Where do good ideas come from?What can we
do to enhance the flow of good ideas? When do we know thatthe design is done?
In my graduate
courses on geometricalmodeling and computer-aided design, these kinds of
questions and the correspondingexercises that I discuss in this paper often
involve an inductive stepgoing from a 2-dimensional form to a related 3-dimensional
shape, or froma configuration of n elements in a highly symmetrical arrangement
to aconstellation of n+1 and more such elements. Each problem was first solved
to my own satisfaction to gain an idea of its possibilities and difficulty.
I then clarified the design task and curtailed the solution space so that
a structured exercise resulted. Typically, these tasks are attacked bythe
students in two waves: First they are simply given the short, open-endedproblem
statement and are asked to think about it and bring their ideasand questions
to the next class. In a joint discussion we then agree onthe salient features
that the solution should have and identify some criteriaby which we could
judge the quality of the various designs. In spite ofthe stated constraints
and of the focussing effect of our discussions,I normally have the pleasure
to obtain new and unexpected solutions thatadd to the richness of the problem
and transcend the previously known solutions.Often I find out later that
others had pondered the same questions, andsometimes even wrote a whole book
about related issues -- as in the caseof the delightful book "Orderly Tangles"
by Alan Holden [
6].Since
the exercises often lead to artistically interesting and pleasingresults,
they should be particularly well suited for this conference, bridgingthe
gap between logic and the arts.
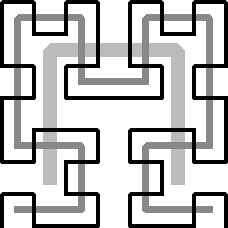
Hilbert Curve
An exercise
that datesback to 1983 [
9
,
10]asks the students to
develop a 3-dimensional, recursive, self-similar,space-filling, piece-wise
linear path inspired by the 2D Hilbert curve[
5] shown in
Figure1b.
This Peano curve, which in the limit fills the unit square, wasdiscovered
in 1891. It can be nicely described by a recursive procedure.The problem
statement makes it implicitly clear that we want the new curveto visit all
the grid points of a cubic array with 2
n x 2
nx 2
n
points so that no grid point has more than two line segmentsattached to
it. The basic approach is fairly obvious: The overall cubeis split into eight
equal octants which are visited in a particular sequence.These octants are
split into octants again, which are then visited in thesame geometric order.
All the interesting issues lie in the details!
After the students
have ponderedthe question for a while, we start discussing desirable criteria
that onemight use to rank-order different designs. For instance, the higher-order
Hilbert curves should maintain the symmetry of the starting frame, andthat
symmetry should be as high as possible. The 3D solution may well havemore
symmetry than the 2D curve. To achieve that goal, we might want tomodify
the top level of the recursion in the original Hilbert curve sothat it forms
a closed loop, thus introducing a second axis of mirror symmetryand leading
to a prominent "H" in the second generation (
Fig.3a).Other aesthetic considerations may suggest that the extra-long
line segmentof three unit lengths occurring near the center of the 3rd-order
planarcurve should be avoided. Ideally one might want to avoid even two subsequent
collinear line segments. Similarly, one might want to minimize the number
of subsequent elements that lie in the same plane. While three subsequent
coplanar segments cannot be avoided, if we want to visit all eight corners
of a unit cube, sequences of more than three segments may be avoidable.Ideally
we would like to find a simple recursive formulation for such astructure.
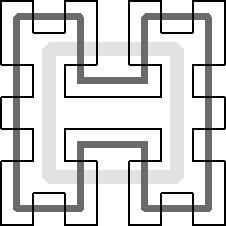

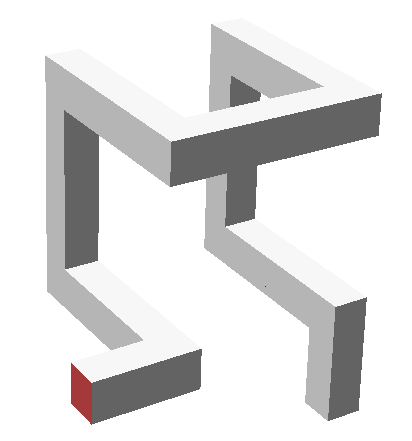
A plausible starting
frame consistsof the closed loop shown in
Figure3b. To use this frame as the basic corner element at the next level,
one of its eight segments, i.e., the dark one in the lower part of
Figure3b, must be opened up, and two new connections to adjacent, identical
corner elements must be created by suitably twisting the L-elements thatwere
formerly attached to it (
Fig.3c
),we place eight such modules, reduced to half-size, into the eight octants
of the original cube. They have to be properly oriented, and some unitshave
to be mirrored (shown darker in
Fig.4a) so that they can be connected readily with their neighbors. This
should be done in such a way that a closed path results that basicallyfollows
the path of the original frame (
Fig.3b).I have built a physical implementation of such a second generation
structurefrom 64 plastic 3/4-inch pipe corner pieces. The problem with constructing
larger physical structures lies in the fact that, regardless of the level
of recursion, two halves of the sculpture are connected only with eithertwo
or four pipe segments, which renders the physical structures ratherweak.
On the other hand, in the virtual space of computer modeling, theprocess
can be continued without limits using ever smaller copies of theoriginal
module. The basic design can then be turned into an impressivevirtual sculpture
with a suitable choice of pipe dimensions, texture, andcoloring (
Fig.4c).
For Hilbert curves
of orderthree and higher, some interesting choices have to be made. I was
ableto design a 512-segment 3D pipe in which there are never more than three
coplanar line segments. However, I had to start with a different cornerelement
for the 2nd-generation curve. Rather than removing the dark segmentin the
base frame (
Fig.3b),I chose
to remove one of the elements adjacent to it (of which there arefour to start
with) and to orient the connecting L-pieces so that theyturn away from the
plane last visited inside the base-frame. These cornerelements now show C2
symmetry around the mid-point of their middle segment,and they can now be
properly oriented in all eight corner positions toform a 2nd-generation Hilbert
path (
Fig.4b).To produce
the corner element for the 3rd generation, we again break opena segment near
one of the corners and suitably twist the adjacent L-elementsoutwards. This
unit can then be assembled into a symmetrical closed loopwith carefully chosen
orientations and mirroring operations. The drawbackof this solution is that
the connection operation needs to modify one ofthe lowest level corner elements,
thus a simple recursive composition ofeight identical corner elements is
not possible.
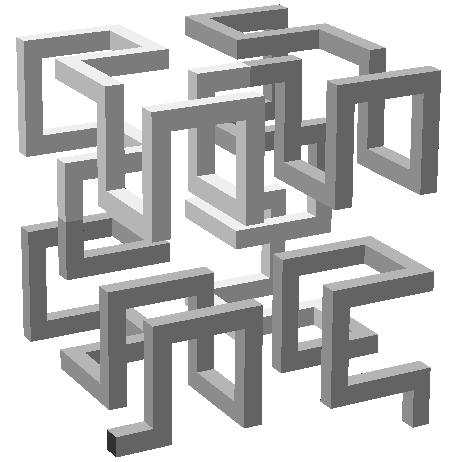


The solution presented
in
Figures4a,c, has the same
basic symmetry, but it exhibits sequences of foursubsequent coplanar pipe
segments; on the other hand, I was able to describeit with a nice recursive
formulation. If a closed curve is desired, thenone has to change the orientations
of the first and last corner elementsat the top level of the recursive procedure.
The approach generalizes tohigher dimensional cubes [
3].The initial starting frame can always be seen as an n-bit reflected
Graycode which runs through all permutations of an n-bit string in such a
waythat each string differs from its predecessor in only a single bit. Scaled-down
versions of this traversal of the starting frame are then placed -- withsuitable
orientation -- into each "corner" of the original hyper-cube.
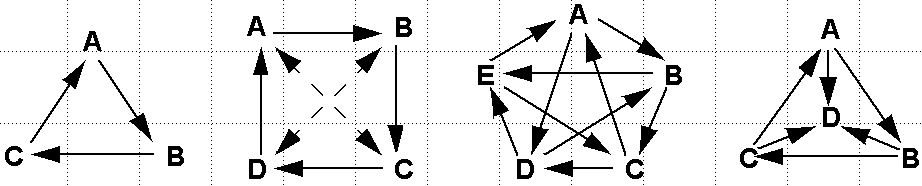
Symmetrical Constellations of Interlocking Loops
Two
tightly intertwinedrings form a simple yet intriguing configuration that
seems to have symbolicmeaning in several cultures (
Fig.5a).An attempt to place three loops in space as compactly and as
symmetricallyas possible, leads to an arrangement known as the Borromean
rings (
Fig.1a,
Fig.5b). Individual pairsof rings are not actually interlocked; the configuration
only holds togetherwhen all three rings are present. However, when we try
to place three perfectlytoroidal rings into a constellation of high symmetry,
the result is a pairwiseinterlocking configuration with three-fold symmetry
(
Fig.5c).
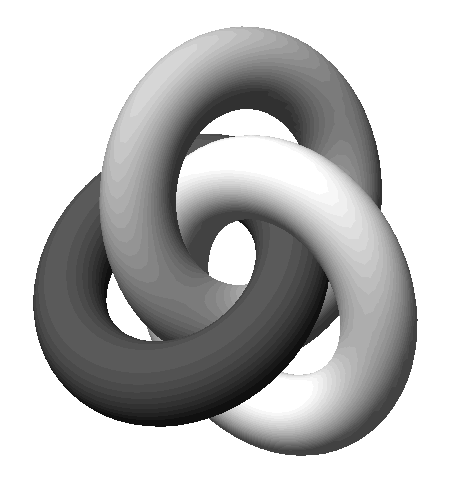
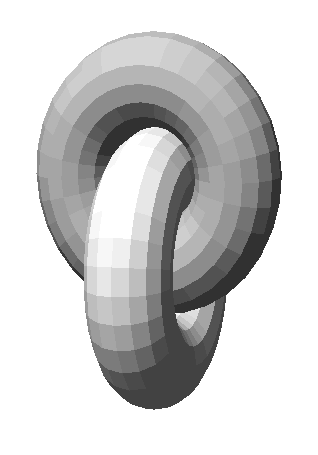

Next, we aim to
cluster morethan three rings around the origin, without much concern whether
individualpairs of rings mutually interlock. The task given to the students
was tofind a constellation of four loops with the highest possible symmetry.
Every loop should be in an identical position within the constellation,so
that the basic symmetry operations transpose any one loop into any otherloop.
If one has not
seen the solutionbeforehand, this problem turns out to be surprisingly difficult.
Two approacheshave proven helpful to guide the students to finding a solution.
The firstone is to ask what symmetry groups one might possibly expect. After
somecontemplation, one finds that with four rings it has to be the tetrahedral
or the octahedral group. The second approach starts with the notion thatone
might want to interlock four triangles. The choice of triangles torepresent
the loops seems natural, because each loop has to interact withthree other
loops, and if we want to do this in a symmetrical manner, weshould choose
a loop with 3-fold symmetry. Given that we want to placefour triangles symmetrically
in 3D space, we need to define the positionsfor twelve vertices -- in a symmetrical
manner. So the question then turnsto how one can place twelve vertices uniformly
and symmetrically onto thesurface of a sphere. The insight to this secondary
problem might come fromthinking about the densest sphere packing, or from
contemplating the Platonicand Archimedean solids and looking for the occurrence
of the number 12-- preferably in an object with tetrahedral or octahedral
symmetry. WhenI initially contemplated this problem, I first thought of the
twelve edgeson a cube. So I placed the vertices at the midpoints of these
edges andconnected them into 4 triangles -- and the solution emerged almost
immediately(
Fig.6a).
I implemented
this configurationas a physical sculpture from 4-inch cardboard tubes [
9],spray-painted with copper enamel on the outside, and with a touch
of fluorescentyellow near its center-- which made the sculpture glow on the
inside whenhit with indirect sunlight (
Fig.6b).It should be pointed out, that in this arrangement every pair
of trianglesmutually interlocks; cutting away one triangle would still leave
the otherthree entangled. Also, the topology of
Figure6b is the mirror image of that of
Figure6a.
I continued my
quest by lookingfor constellations of five and more intertwined loops. For
five loops,an extension of the process that had helped me find the 4-triangle
structurewas employed -- i.e., I tried an inductive approach. Each of the
five loopswould have to interact with four others, thus using squares seemed
likea reasonable start. This then required twenty vertices positioned symmetrically
in space. The twenty vertices of the pentagon-dodecahedron offered themselves
conveniently, and it did not take long to find a grouping of the vertices
into four planar polygons -- which however were rectangular rather thansquare
(
Fig. 6c). Alsothe resulting
constellation does not carry the full symmetry of the Platonicsolid from
which it was derived, it just has one axis of 5-fold symmetry(C5) and five
axes of C2 symmetry.
It is interesting
to study theinterlocking pattern of this structure. No two rectangles interlock!
Itlooks like a more complicated Borromean arrangement in which each loopsurrounds
exactly two other ones in a cyclical relationship. Encouragedwith this result,
we might try again to look for a Borromean arrangementwith four loops. However,
a little conceptual reasoning will soon let ussee the difficulty of this
quest. Let's use the notation A ---> B to indicatethat loop A encircles
loop B on the outside. Thus the Borromean rings havethe cyclic relationship
indicated in
Figure7a. If
we try to draw a similar diagram for the 4-ring constellation,then we run
into the difficulty that in a complete graph with four vertices,there are
three edges joining at each vertex; thus the number of incomingand outgoing
arrows cannot be made the same everywhere. To draw a symmetricaldiagram in
which all vertices are identical, we would have to use double-headedarrows,
which we can interpret as an indication that the two rings (vertices)connected
by such a double arrow are mutually interlocking (
Fig.7b).On the other hand, the complete graph with five vertices has
four edgesjoining at every vertex, and we can readily draw such a graph with
twoincoming and two outgoing arrows at each node (
Fig.7c).This corresponds to the configuration of five loops discussed
above andshown in
Figure 6c
.
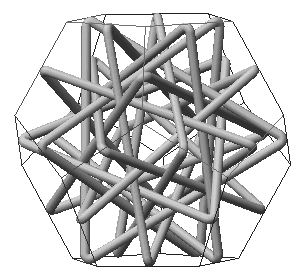
Before I had a
chance to pushmy quest much beyond the constellation with five rings, I stumbled
ontothe delightful book "Orderly Tangles" by Alan Holden [
6].This is an invaluable resource containing dozens of such symmetrical,
interlockingconstellations with as many as twenty loops.
Figure8b shows a computer simulation of a tangle with ten triangles inspired
by a model built by Holden. In this case, the vertices of the triangleslie
on the midpoints of the thirty edges of the dodecahedron. The inductivereasoning
outlined above for the steps from three to four and then to fiveloops can
be continued. Once one understands the search procedure, it isnot too difficult
to find the more complicated tangles.


Holden's book
also containsa Borromean configuration formed by four triangles; its linking
logic correspondsto
Figure 7d
, and it isrealized by a 3-ring Borromean configuration that rigidly holds
in placea fourth, non-entangled triangle (
Fig.8a).Holden also shows how such symmetrical tangles can be carried
beyond justsimple loops; he shows models of interlocking tubular tetrahedral
frames.Another realization of the classical tangle of five tetrahedra with
all20 vertices lying at the corners of a dodecahedron is shown in
Figure8c. This part has been constructed with Selective Laser Sintering
(SLS),one of the emerging layered Solid Free-Form (SFF) fabrication technologies
[
7].
Yin-Yang
Yin-Yang
symbolizesthe two complementary forces that comprise the Tao, the eternal
dynamicway of the universe: Yin is the earthly, dark, passive, or female
principle.Yang is the heavenly, light, active, or male force. Geometrically,
theYin-Yang symbol divides a circle into two complementary halves that in
some sense are "opposites" of one another. The task given to the students
was to find a corresponding partitioning of a sphere in 3-space. The richness
of the solutions proposed by the students in the Fall 1997 course CS 285,
Solid Free-Form Modeling and Fabrication, was unusually rewarding (
Fig9,
Fig.10).

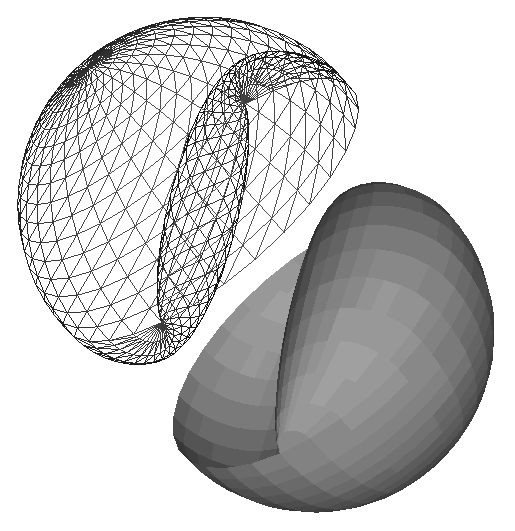

The most often
proposed solutionwas a sphere cut into two halves with a "band-saw" following
the path ofthe 2D Yin-Yang dividing line. Some solutions were offered as
clay models(
Fig.10a), others
as machinedparts (
Fig.10b
), or assophisticated computer renderings (
Fig.10c).While I feel that this is not the best solution, since it is
just an extrudedextension of the 2D figure, this is also a shape celebrated
by great artistssuch as Max Bill (
Fig.10d).




Still, I was more
intriguedwith attempts to cut the sphere with a surface that curves in both
directions.A key question then arises: should the two halves be identical
or mirrorimages? The most innovative proposal came from a couple of students
whoreasoned, that the true analogy of going from 2D to 3D demanded that the
sphere be cut into three identical parts -- possibly colored with the three
primary colors red, green, blue.
The crucial characteristics
to order and classify this plethora of shapes is the symmetry of the surface
that divides the sphere. The following fundamental possibilities exist:The
trivial solution cuts the sphere with a plane through its center; butthis
does not exhibit any features of the Yin-Yang icon. A more interestingclass
of dividing surfaces has C2 symmetry with respect to some axis throughthe
sphere center; this results in two congruent halves (
Fig.9a,b).The "band-saw-cut" solutions (
Fig.10)also fall into this class. A generalization allows C3 symmetry
around thisaxis and would thus cover the case of three identical subcomponents.
Thethird and, to me, most interesting class, has glide symmetry, which brings
the dividing surface back onto itself when it is rotated 180 degrees andthen
mirrored on a plane perpendicular to that axis; this leads to complementary
mirror-parts (
Fig.9c).This
shape is most defensible on philosophical grounds; we want to createtwo halves
that are not identical but rather complements of one another.The most beautiful
formulation of such a shape (
Fig.12a)is composed of three spherical surface pieces and two cyclides
[
2].This shape was also discovered
by C. E. Peck in 1992.



Attempts at machining
such ashape on a milling machine run into the problem, that the part shows
aconcave groove that leads into a point with infinite curvature, which cannot
be cut with any tool of finite dimension. The 2D Yin-Yang has constantcurvature
and uses only circles of two radii that differ by a factor oftwo. I found
a corresponding solution in 3D that replaces the two cyclidsurfaces with
two tori in which the major radius R is twice the size ofits minor radius
r. This shape can readily be described as a Boolean expressionof its five
curved shapes and a few half-planes. The resulting shape isshown in
Figure 12b, andan early attempt at machining it on a milling machine
in
Figure12c.
Spiral Surface
The
logarithmic spiral(
Fig.13a
) is a fascinatingcurve, and may be considered the ultimate solution to self-similarity
atarbitrary scales. As in the first problem dealing with the Hilbert curve,
we might ask what an analogous curve through 3D-space might look like.One
might argue that a 3D spiral curve should (eventually) pass throughall possible
directions emerging from the origin of the coordinate system,and, at the
same time, gradually move outwards at an exponential rate.The problem of
visiting all points on a sphere with a continuous smoothpath has been addressed
by Dan Asimov's "Grand Tour" [
1],which, given a long enough time span, will approach every point on
thesurface of a sphere with arbitrary closeness. All we have to do, is to
let the radius grow exponentially as a function of time.
This problem has
not been presentedto any student yet. The way I approached it myself was
to make a wire skeletonfrom pipe cleaners (
Fig.13b)that contained the three coordinate axes (black) and three spirals
in thethree main coordinate planes (white). Additional pipe cleaners (grey)
producedsome connectivity among these spirals and formed partially spherical
shells(
Fig.13c). It became
clearthat it was not possible to connect all spiral branches smoothly with
oneanother; some jumps from one "onion shell" to another had to occur. Thus
the surface cannot be totally closed. It turns out that this is a usefulfeature,
since it would be rather dull, if we could not view the internalstructure
of this surface. Later it became apparent that the edges thathad to be introduced
to avoid the discontinuous jumps from one shell tothe next inner/outer one
could themselves take on the shape of spirals.What serendipity!
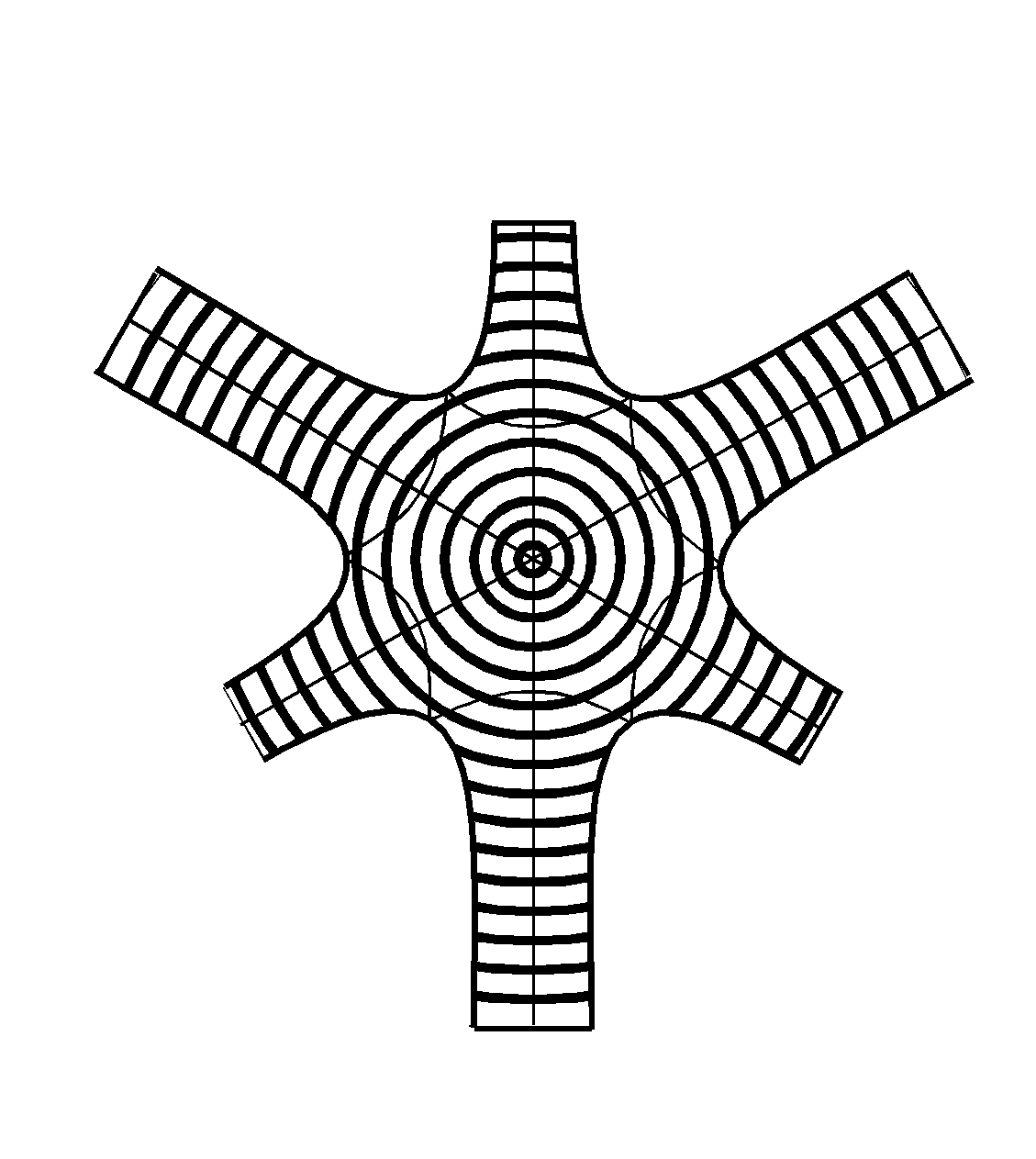

One emerging solution
exhibitedD3-symmetry along the {111} space diagonal in the coordinate system
inwhich I had placed the original three spirals; and it showed six openings
with helical edges leading inwards toward this axis. At this stage, I started
to build paper models to get a better feeling for the surface topologyitself.
I designed the spider pattern shown in
Figure14a and made several suitably scaled copies. These were joined
togetherin a nested manner, where the long arms of one spider join the short
armsof the next larger spider. The result is shown in
Figure14b.
Subsequently this surface was
modeled on the computer. Using three Bézier patches to form theshape
of one "L" with a 60-degree corner, it takes 18 patches to composeone complete
spider (
Fig.14a).The boundary
constraints to guarantee smooth continuation of the patchesare not hard to
derive; and the inner control points of the cubic patchesare adjusted to
minimize any apparent bumps. Finally, Jane Yen added highlightsand shadows
and rendered that surface (
Fig.15a,b
)with the Blue-Moon Rendering Tools [
4].The next step is to make the surface thicker and to derive a solid
descriptionfrom which a 3D model can then be built with one of the layered
Solid Free-Form(SFF) fabrication techniques [
7].


Fig.15: a)
Virtual model of Spiral Surface, b) half that surface showing spiralcurve
in cross section.
Discussion and Conclusions
The
design exercisesdiscussed in this paper are a good example of an activity
that bridgesthe realms of logical reasoning on the one hand, and of intuitive
and evenartistic contemplation on the other. The region between art and mathematics
is particularly suitable to study the creative process on (somewhat) open-ended
design problems. The problem statements are loose enough to allow the mind
to roam free and to come up with potentially wild and unorthodox solutions.
At the same time, these geometrical puzzles possess enough structure andquantifiable
properties so that one can apply an acceptable metric to theresults and rank-order
different solutions. This process brings wild, far-flung,non-sequitur creativity
into a more disciplined mode where there are designsolutions of defensible
quality.
The presented
problems startwith the construction of a simple one-manifold, the 3D Hilbert
curve, whereconnectivity, symmetry, and a recursive formulation are the dominant
concerns.The subsequent tasks increase in complexity, adding topological
considerationsof linking behavior, and evolving from one-manifolds (curves)
to two-manifolds(surfaces).
The methods employed
to tacklethese problems vary, but a dominant role is played by inductive
reasoningand a judicious use of symmetry. The key challenge of the 3D Hilbert
curveis to find a recursive formulation to build a generic corner element
withthe desired connection properties at the corners so that the connectivity
among the eight octant cuboids stays the same in each generation. In searching
for orderly tangles of interlocking loops, it was most productive to determine
the expected symmetry group, and then place a suitable number of vertices
evenly onto the surface of a sphere so as to span the polygonal implementations
of the loops. For the two surface-related problems, paper and pencil, oreven
computer drawings did not seem adequate to explore the potentiallyvery large
solution space. The use of clay, wire-mesh, and/or pipe-cleanersseemed to
help a lot in the visualization of the problem and its possiblesolutions.
What all the solutions
havein common is that the "best" solutions in terms of maximum analogy with
the starting shape also have a high aesthetic appeal by themselves -- which
adds a special bonus to these exercise tasks. This bonus becomes even greater
with the advent of solid free-form (SFF) manufacturing technologies thatallow
to turn these virtual design artifacts into nice physical sculptures.
Acknowledgments
Some
aspects of thiswork were partially supported by the National Science Foundation
undera research grant to study the designer/fabricator interface for rapid
prototypingof mechanical parts. The help of Jane Yen and Jordan Smith with
the renderingof some of the virtual sculptures is also gratefully acknowledged.
References
-
D. Asimov, "The GrandTour: A Tool For Viewing Multidimensional Data." SIAM
Journal of Science& Stat. Comp., Vol. 6, pp. 128-143, (1985).
-
W. Boehm, "On Cyclidesin Geometric Modeling." CAGD, Vol 7, pp. 243-255, North
Holland, (1990).
-
E. N. Gilbert, "GrayCodes and the Paths on the N-Cube." Bell System Tech.
Jour. 37, pp. 815-826,(1958).
-
L. Gritz, "Blue MoonRendering Tools Home Page," http://www.bmrt.org/
-
D. Hilbert and S.Cohn-Vossen, "Geometry and the Imagination." Chelsea, New
York, 1952.
-
A. Holden, "OrderlyTangles." Columbia University Press, New York 1983.
-
D. Kochan, "SolidFreeform Manufacturing: Advanced Rapid Prototyping." Manufacturing
Researchand Technology 19, Elsevier, Amsterdam, New York, (1993).
-
C. Mead and L. Conway,"Introduction to VLSI Systems." Section 1.15, Addison
Wesley, Reading MA,(1980).
-
C.H. Séquin."Creative Geometric Modeling with UniGrafix." Technical
Report UCB/CSD83/162, U.C. Berkeley, CA (Dec. 1983).
-
C.H. Séquin."More... Creative Geometric Modeling." Technical Report
UCB/CSD 86/278,U.C. Berkeley, CA (Dec. 1985).
VisMath HOME