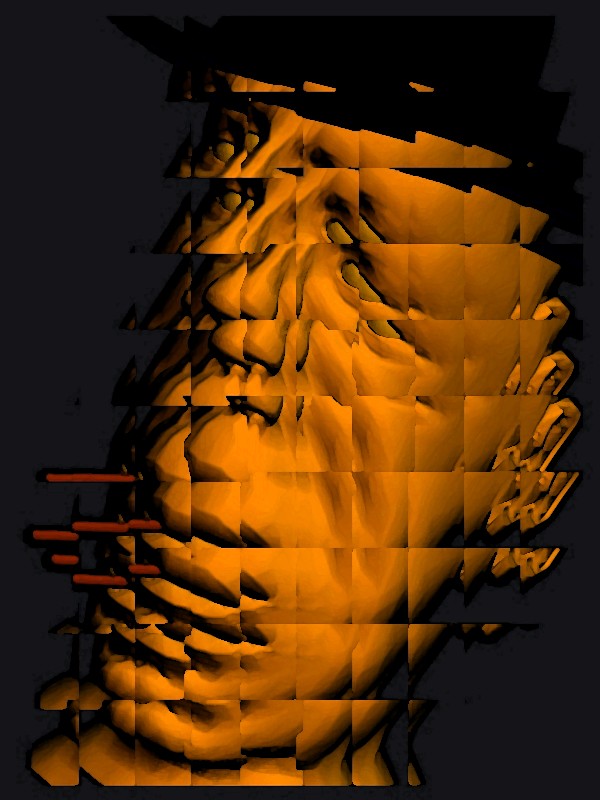
|
Rendering of Abstract Digital Images Jeffrey Smith and Ergun Akleman Visualization Sciences Program Richard Davison Department of Architecture John Keyser Department of Computer Science Address: Visualization Laboratory 216 Langford Center, Texas A&M University College Station, Texas 77843-3137, USA. Email: ergun@viz.tamu.edu
Abstract
1. Introduction This paper presents the MultiCam system which provides interactive feedback to artists designing abstract paintings with a simple, interactive and intuitive rendering technique. In this system, multiple distinct views of a 3D scene are combined into a final image. The viewing area is initially divided into a grid of randomly jittered and overlapping viewports, each containing a unique view of the object. When combined, these views form a composite view of the object that has been hardware-rendered from many cameras. In our system, a wide variety of parameters including
the number of cameras, their fields of view, their positions in the 3D
space, background colors, textures, warm and cool light intensities, and
silhouette edge thickness can be controlled by artists. The ability to
control these parameters in real time enhances the artists' ability to
create unique abstract images with a variety of styles including cubist
and surrealist. Examples of cubist and surrealist-like MultiCam
paintings, designed by the authors, are shown in Figures 1.A
and 2.A. The resolution of the images created by our
system is limited by the screen resolution. Moreover, these images do not
have the noise that is very common in actual paintings. They can, therefore,
serve as base paintings and can be used as a point of departure for an
abstract painting. These base paintings can be further improved and manipulated
by artists either by using computer paint programs as shown in Figures
1.B
and 2.B or by hand as shown
Figure
3.
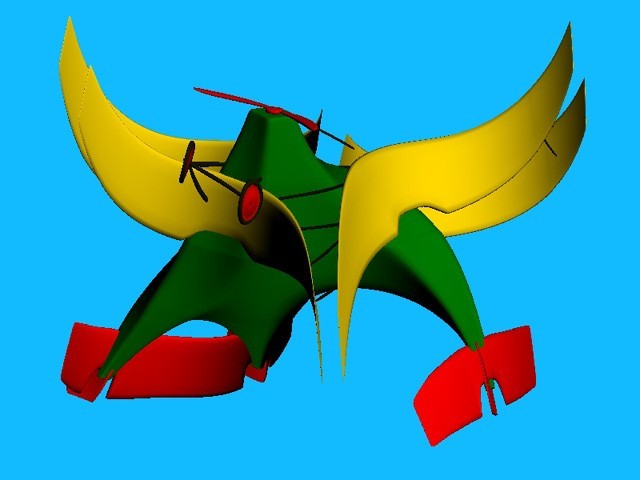
Figure 1: (A) An example of a cubist-like
painting that can be interactively created using our system.
Figure 2: (A) An example of a surrealist-like
painting that can be interactively created using our system.
Figure 3: (A) is reprint of an original MultiCam
rendering that was worked over with
2. Inspirations and Contributions MultiCam allows artists to design their own paintings by explorations using an abstract computer graphics rendering system that is based on the cubist principles of multiple views and collage. This interactive system is inspired by multiple view ray-tracing techniques introduced simultaneously by Glassner [6] and Meadows-Akleman [12,1]. These two techniques generalize ray-tracers by allowing a different camera position for each pixel. Although it is easy to create interesting abstract paintings with these methods, the major disadvantage is that they do not allow interactivity since they are based on ray-tracing. The main difference between the two techniques is the user's ability to control camera parameters. Glassner uses free-form surfaces to control camera parameters; Meadows-Akleman uses RGB colors of the images. The advantage of free-form surfaces is that they allow total mobility of the cameras. Using images limits the camera parameters; for instance, cameras stay inside a bounding box. On the other hand, the advantage of images is that they can allow discontinuities in camera parameters which are important in the creation of fragmented (or faceted) images. Our technique is an interactive and discrete version of
Glassner's method. We allow the artists to control camera parameters using
free-form surfaces, but instead of a continuous camera space we use a discrete
space, i.e., we allow only a finite number of cameras which can be hardware-rendered
using OpenGL. Moreover, with a finite number of cameras we
can obtain fragmented images as in the Meadows-Akleman method. Unlike Glassner
and Meadows-Akleman, our method employs another cubism-based concept: collage.
Using our system, artists can manipulate how the images, which are obtained
from each camera, are composed in the image space.
3. Related Work This paper draws influence from many areas of traditional and computer artwork. The non-representational nature of the work is based on ideas and methods first explored by late-nineteenth and early-twentieth century artists, as well as in early computer art. The work presented here is also related in its non-photorealistic and non-objective nature to many studies in various computer graphics and digital image rendering methods. In the nineteenth century, many renaissance conventions of picture making began to break down in art [15]. Cezanne is one of the first modern painters to break from the use of traditional perspective. A significant departure from traditional realistic methods of painting came with the Cubist painters [3]. Their paintings were characterized mainly by a new way of handling space: a volumetric structure in which depth was flattened and objects and their surrounding environment were often simplified into many facets. Objects were often depicted from many sides at once using multiple views. Cubists also introduced collage to painting by adding non-painted objects (collage elements) to the surface of the canvas. Futurists developed a style to incorporate the movement through time and space into multiple-view compositions [15]. One of the best known futurist painting is Duchamp's "Nude Descending a Staircase", in which the movement is represented by multiple views, each representing a successive motion of a figure walking down a staircase [3]. In recent years, Hockney produced multiple view photographic collages that are composed of Polaroid and 35mm photographic prints [10]. The fragmented composition and multiple perspectives of Hockney's collages are reminiscent of a Cubist style, and produced a painterly feel in the work, instead of photographic realism. In computer graphics, many early attempts at creating artwork with a computer were abstract, due to the limited capability of early graphical displays [8]. However, with the advent of more sophisticated software programs and graphical displays, the efforts of computer scientists turned more toward the creation of photorealistic images. During the last decade, non-photorealism again becomes popular [Gooc2001]. In 1990 Haeberli developed the first painterly rendering system [9]. Since then, a large variety of painterly rendering approaches such as [5, 11] have been developed. Although there has been an increasing interest in more artistic and non-photorealistic approaches, only a few truly abstract rendering approaches have been developed to create abstract paintings. In 1991, Sims created a system of artificial evolution to produce wildly abstract digital images [17]. Snibbe and Levin performed experiments in abstract computer graphics by developing a 2D interactive dynamic abstraction system [19]. Only a few applications have been developed that use cubist
ideas, multiple perspectives and simultaneous views. The digital artist
Utterback in 2000 devised an interactive installation that explored the
idea of cubism as it applied to video sequences [20].
Glassner devised a free-form "Cubist" camera system [6]
using a commercial 3D modeling and rendering package. The system
uses raytracing to render images, taking one unique viewpoint for each
pixel in the final image. Viewing vectors are produced by sampling points
from the surfaces of two NURBS planes, one designated as the "eye" plane
and another as the "lens" plane. Meadows-Akleman developed an abstract
rendering approach, known as camera painting [12,1],
that used the color information from digital images to distort 3D
scenes rendered with raytracing. The system uses the r,g,b color components
of digital images to replace the x,y,z coordinate information of the camera
position and orientation for each pixel in a raytraced image. The output
produced is an abstraction of a normal raytraced scene, controlled by an
input image of the user's choice. In this way, control over the final image
is based on the user's production of the input image by means of painting
or photography, or selection of other imagery. Although interesting looking
images can easily be created using the Glassner and Meadows-Akleman techniques,
these methods do not allow interactivity.
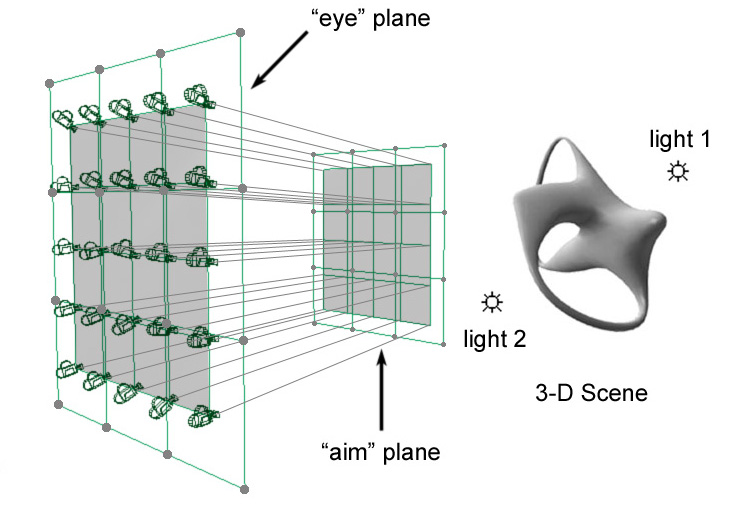
4. Methodology and Implementation Our interactive technique for creating abstract images is based on simple and widely available 3D modeling and rendering methods. Our system was developed using C++ and OpenGL [14]. Its user interface is built using the Fast Light Toolkit (FLTK). The current MultiCam system is running on IRIX and LINUX operating systems, but, because of the flexibility of FLTK and OpenGL, the system is portable to other operating systems. The main application window of MultiCam consists of a drawing area, in which the image composition can be viewed and updated, and a side option panel, which contains menu bars that display the many options for creating what appears in the drawing area. The interface provides an organized set of controls that the artist may use to execute procedures that create abstract images from any given 3D scene. A 3D scene in the MultiCam system
is a 3D space that contains a number of 3D polygonal objects,
a number of cameras from which the models can be viewed, and lights (Figure
4.A). The system does not support shape modeling, i.e. the polygonal
objects in the scene are created in separate modeling software. Except
for the shapes of polygonal objects, all other properties of the scene
including the number of cameras, their positions and orientations, the
light colors and the material properties can be controlled by the users.
The polygonal objects are imported into the MultiCam system
via the Wavefront OBJ file format. Their shapes cannot
be changed, but, the objects can be rotated, translated and scaled through
mouse controls using code derived from the "Arcball" interface
developed by Paul Rademacher.
4.1. Camera Controls. The camera system of MultiCam is based on
the Glassner model [6], which is composed of two camera
surfaces, known as an "eye" surface and an "aim" surface. The eye surface
contains the points at which the cameras are placed, while the aim surface
contains the points at which the cameras are aimed.
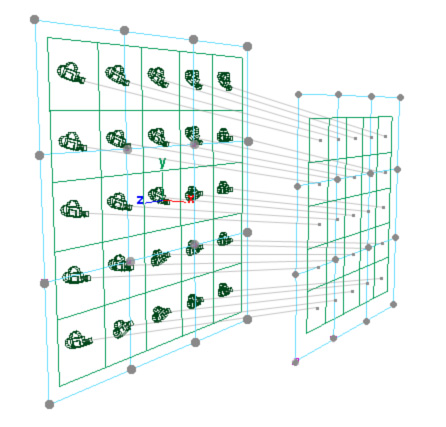
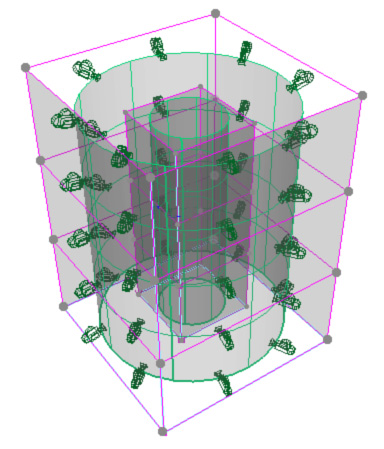
Figure 4: (A) MultiCam scene description and examples
of multiple-camera "eye"
The camera eye and aim shapes are two free-form surfaces that are defined by a set of control cameras that are given by two (eye and aim) points. Currently, we use sixteen control cameras and uniform bi-cubic splines [2] and Bezier surfaces[16] are available options for free-form surface creation. Example free-form surfaces include planar or cylindrical surfaces (see Figure 4.B and 4.C). We allow the camera system to contain differently-shaped eye and aim surfaces, (e.g. an eye sphere and an aim plane). The user can freely move control cameras in the 3D object space through mouse and keyboard interaction. Options are available allowing the user to specify in which direction to translate and about which axis to rotate. The positions and orientations of the actual cameras are
determined by uniformly sampling u and v parameters of the free-form surfaces.
The sampling frequency is determined by the number of cameras in the u
and v directions. The number of cameras can be changed by the users
anytime through sliders. The users can also modify these individual camera
positions and orientations by "jittering". The camera jitter option disrupts
the regular placement of the cameras by adding two random vectors to be
added to the placement of eye and aim positions of each camera.
4.2. Collage Control Our system uses the GL scissor test to create a collage of images that are rendered by each camera. The GL scissor test is an OpenGL technique that allows the display window to be divided into many viewports [14]. By default, this 2D collage gives a simple grid in which each grid square contains a unique view of the scene as seen by one of the cameras. Each window shows an updated view of the object as it is rotated or translated interactively. The user can change the sizes of images, can randomize their positions and can add z information. These controls add a sense of movement and rhythm to the resulting collage image. MultiCam allows the users to implicitly
control the placement of the images in the collage. In MultiCam,
even these collage images are considered to form a free-form surface that
can be folded over itself in two-dimensions. The user can control the 2D
placement
of collage images by moving the 2D positions of sixteen control
points. Uniform bi-cubic splines [2] and Bezier surfaces[16]
are again available options for free-form surface creation.
4.3. Lighting and Rendering Controls An artist's control over the composition of an image depends largely on the choice of a color scheme and lighting parameters. To light the objects in the scene and enhance the artist's choice of color, a warm-cool lighting system is included, based on the system developed for technical illustration and adapted to use OpenGL functions by Gooch, Gooch, Shirley, and Cohen [Gooc2001]. The user has the choice of using one or two lights, one designated as warm and the other as cool, and is also able to interactively choose their color. To enable a modulation effect similar to the technique used by Cezanne and other cubist painters, warm and cool light colors and intensities are allowed to mix across the surface of the object, adding a rich color effect to the object through a smooth color transition. This effect, along with the fragmented multiple-camera view, creates a modulation effect in which colors pass from one hue to another through mixing in gradual steps. To incorporate the use of line into the MultiCam drawing system, a "silhouette" edge drawing option is included, which provides an outline. The use of silhouette outline is meant to emulate the use of line by Cezanne and the cubist painters. The silhouette edge utility allows the user to experiment with line weight by specifying the color and thickness of the object's outline. To create the silhouette edge the models are drawn twice in OpenGL, once in wire-frame mode without lighting calculations to create an outline, and another time with normal lighting calculations, drawn over the wire-frame image. Surface properties, such as color, shininess, and texture,
as well as the color of the background are also important to an object's
appearance. In MultiCam, the user can select a static background
color. The surface properties can either be imported within OBJ
file or can be manipulated by the users in the MultiCam interface.
The system also allows texture mapping, resulting in increased detail.
A texture mapped example is shown in Figure 5.A.
4.4. Saving Still Images and Creating Animations To save single images, a function to write TIFF
(Tagged Image File Format, copyright Adobe Systems, Inc.) files has been
included. The images in Figure 5 show two cubist caricatures
of Humphrey Bogart that were created and saved using MultiCam.
In addition to saving individual still images, abstract animations can
also be created and saved as a set of image frames. Abstract animations
are created by interpolating key-framed collage controls and scene parameters
such as shape transformations, eye and aim positions of control cameras,
and material and light properties.
Figure 5: (A) A textured example, interactively
created in the MultiCam rendering system by Jeffrey Smith.
5. Conclusion and Future Work In this research, a tool has been developed that allows artists to experiment with multi-perspective viewing parameters in real-time through mouse-driven control of the size and shape of camera surfaces. Through an efficient and user-friendly interface, artists can adjust color and lighting information, material properties, and drawing techniques. In addition, artists cancontrol the multi-perspective camera properties of a 3D scene. The real-time nature of the MultiCam viewing mechanism allows artistic computer image manipulation to take on an interesting mixture of 2D and 3D forms in the same interface, providing a unique system for creating computer-generated art. Future research endeavors in the area of MultiCam rendering for artistic purposes can include a number of options for improving the functionality and increasing the flexibility of the MultiCam software. Alternatively, the camera surface information can be exported to separate, more sophisticated photo-realistic rendering software. 6. Acknowledgments We are thankful Stephen Parker and Han Lei for allowing
us to use their 3D facial models. The silhouette edge utility is
based on code developed by Vinod Srinivasan. The function to write TIFF
files is adapted from the TIFF library specification in code written
by Michael Mistrot. We are also thankful to anonymous reviewers for their
helpful suggestions.
References [1] {E. Akleman and S. Meadows, "Camera Painting", webpage: www-viz.tamu.edu/faculty/ergun/research/artisticdepiction/ [2] R. H. Bartels, J. C. Beatty, and B. A. Barsky, An Introduction To Splines for Use in Computer Graphics & Geometric Modeling. Los Altos, Calif.: Morgan Kaufmann Publishers, Inc., 1987. [3] D. Cooper, The Cubist Epoch. New York: Phaidon Publishers, Inc., 1971. [4] P. Cooper, Interpreting Cezanne. London: Tate Publishing, 1996. [5] C. Curtis, S. Anderson, K. Fleischer, and D. Salesin. "Computer-Generated Watercolor", Proc. SIGGRAPH '97, pp. 421-430, Aug., 1997. [6] A. Glassner, "Cubism and Cameras: Free-form Optics for Computer Graphics", Microsoft Technical Report, MSR-TR-2000-05, http://www.glassner.com/andrew/cg/ research/cubism/cubism.htm [7] A. Gooch, B. Gooch, P. Shirley, and E. Cohen, "A Non-Photorealistic Lighting Model for Automatic Technical Illustration", Proc. SIGGRAPH '98, pp. 447-452, Aug., 1998. [Gooc2001] B. Gooch and A. Gooch, Non-Photorealistic Rendering. Natick, Mass.: A.K. Peters, Ltd., 2001. [8] C. Goodman, Digital Visions Computers and Art. New York: Harry N. Abrams, Inc., 1988. [9] P. Haeberli, "Paint by Numbers: Abstract Image Representations", Proc. SIGGRAPH '90, pp. 207-214, Aug., 1990. [10] C. Knight, "Composite Views: Themes and Motifs in Hockney's Art." David Hockney: A Retrospective. Organizers, M. Tuchman and S. Barron. New York: Harry N. Abrams, Inc., 1988. [11] B. Meier, "Painterly Rendering for Animation", Proc. SIGGRAPH '96, pp. 477-484, Aug., 1996. [12] S. Meadows and E. Akleman, "Abstract Digital Paintings Created with Painting Camera Technique", Proc. D'ART 2000/Information Visualization 2000, London, United Kingdom, July, 2000. [13] M. Mohr, Personal website, www.emohr.com/index.shtml. [14] OpenGL Architecture Review Board, M. Woo, J. Neider, T. Davis, D. Shreiner, OpenGL Programming Guide: The Official Guide to Learning OpenGL, Version 1.2. Reading, Mass.: Addison-Wesley, 1999. [15] H. Read, A Concise History of Modern Painting. London: Thames and Hudson, 1974. [16] D. Rogers and J.A. Adams, Mathematical Elements for Computer Graphics. New York: McGraw-Hill, Inc., 1976. [17] K. Sims, "Artificial Evolution for Computer Graphics", Proc. SIGGRAPH '91, pp. 319-328, July, 1991. [18] S. Snibbe, Personal website, www.snibbe.com/scott/index.html. [19] S. Snibbe and G. Levin E., "Interactive Dynamic Abstraction", Proc. NPAR 2000, pp. 21-29, June, 2000. [20] C. Utterback. "Liquid Time: An
Exploration of Video Cubism", SIGGRAPH 2000 Conference Abstracts and Applications,
p. 223, July, 2000.
|