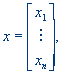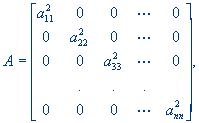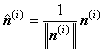|
OF AN ITERATIVE PROCEDURE FOR SOLVING THE
OPTIMIZATION PROBLEM INTO AN ELLIPSOID Liljana Stefanovska
Faculty
of Technology and Metallurgy, P.O. Box 580, Skopje, Macedonia Beti
Andonovic
Faculty
of Technology and Metallurgy, P.O. Box 580, Skopje, Macedonia Sonja
Gegovska-Zajkova
Faculty
of Electrical Engineering, P.O. Box 574, Skopje, Macedonia szajkova@cerera.etf.ukim.edu.mk ABSTRACT.
For solving the problem of optimization in a space limited by an
ellipsoid and a linear goal function, for which the maximum is searched, there
is an iterative procedure suggested. The procedure starts from an interior point
of the ellipsoid and by moving into its interior there is a generated sequence
of points of the contour of the ellipsoid that converges to the optimal solution
(point), where the goal function is of greatest value. 1.
PRELIMINARY OBSERVATION
Let
Rn is Euclidean n-dimensional space where the vector xÎRn is denoted by
where
xi (i = 1, ..., n) are scalars. The
inner product of two vectors x,
y Î Rn is defined by and the norm of an arbitrary vector xÎRn is defined by For
any vector x¹0, there is its unit vector
where
2. SETTING OF THE OPTIMIZATION PROBLEM We observe the optimization problem of the following type max{cTx
| xÎE} E = {xÎRn | xTAx £ 1} (1) where
c,
xÎRn are vectors, A is a
diagonal matrix of positive elements of an order n´n, that is
where
ai (i = 1, ..., n) are
scalars. Such a defined feasible space determines the interior of an
n-dimensional ellipsoid. Not getting more specific, instead of problem (1), we observe the problem of the following type
max{
E = {xÎRn | -xTAx ³
-1}
(2) where
3. AN ALGORITHM OF THE METHOD To
solve the optimization problem (2), there is an iterative procedure suggested
for constructing a sequence of feasible solutions {x(k)}
obtained by the
recurrence formula
x(k+1)
= x(k)
+ t(k) d(k),
( k = 0, 1, 2, ... ).
(3) The vector d(k)¹0 determines the feasible movement direction
into the interior of the ellipsoid, and the scalar t(k)¹0
determines the length of the step which is chosen such that the following
solution is on the contour of the feasible area and thereat a real improvement
in the goal function is achieved. That means that the following inequality is
satisfied
3.1.
THE STARTING STEP The
method starts from an interior feasible solution x(0),
i.e.
- x
(0)TAx(0)
> -1. A starting movement direction is the vector
d(0)
=
and
the length of the step t(0)
is chosen by the condition that the next solution x(1)
obtained by
x(1)
= x(0)
+ t(0) d(0)
(6) satisfies the
following equality
x(1)
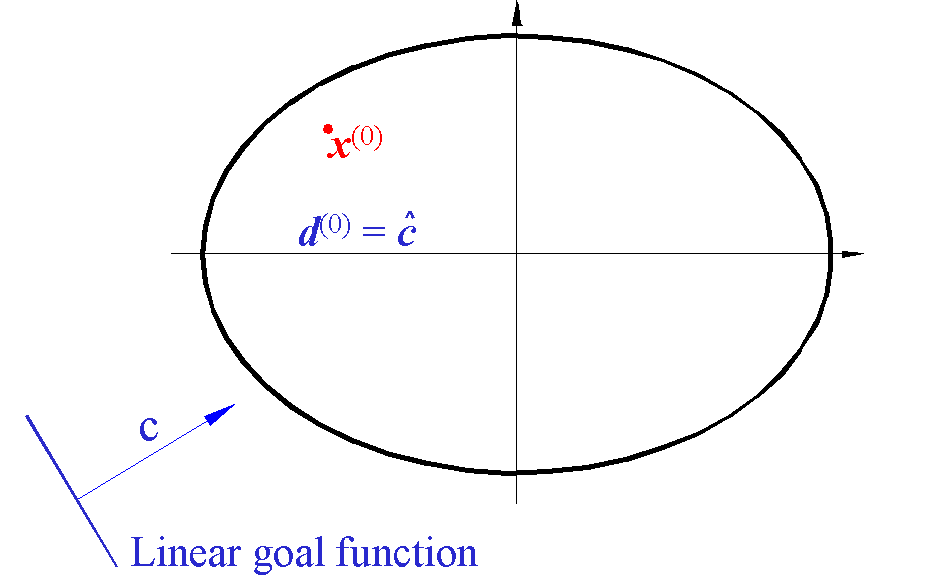
TAx(1) = 1, i.e., to be a boundary feasible solution. The graphic review of this coming out on the contour of the feasible space in R2 is shown on Figure 1.
Figure
1. Indeed,
by choosing the starting movement
direction (5), there is always some small length of the step t(0) >
0, provided by the condition x(0) to be an
interior solution, where for the next solution
x(1)
= x(0)
+ t(0)
the value of the
goal function will be
Thus, for the next solution x(1) the value of the goal function will increase, which means that a better feasible solution is obtained. 3.2. AN ARBITRARY STEP The further determining of the boundary feasible sequence of solutions x(i+1) = x(i) + t(i) d(i) (i = 1, 2, ... ) (7) continues by choosing an upper movement direction and determining the step length. At any feasible solution x(i) determined by (7) and for which holds
x
(i)TAx(i) = 1 there
is the vector n(i)ÎRn, that is perpendicular to the
tangent plane of the ellipsoid at the vector x(i) and
directed to the interior of the ellipsoid. Thus,
and
Lemma:
The direction
d(i)
=
is a feasible movement direction (Figure 2.), by which the goal function increases its value.
Figure 2 Proof: For a length that is small enough t > 0, the next feasible solution is
x(i+1)
= x(i) + t d(i)
= x(i)
+ t (
for which it is true x(i+1)TAx(i+1) = 1 and the value of the goal function
=
achieves a real increasement because
||
To
the sequence of boundary solutions there
is a corresponding sequence of the goal function values { z(i)
}, (i = 0, 1, 2, …) for which it is true z(i+1)
> z(i). The method ends when the following condition is satisfied
|| z(i+1) - z(i) ||
< e .
(10) for
an arbitrary e > 0. 4. EXAMPLE
In R2,
let the goal function vector be and the
ellipsoid is defined by the diagonal matrix where e =0.001 is given. Table 1. Results for the initial solution
Table 2. Results for the initial solution
Table 3. Results for the initial solution
The
results presented above show that the optimal solution is REFERENCES [1]
Bandi, B.,
Metodì optimizacii, Vvodnìi
kurs,
Izd. Radio i svyazy, Moskva, 1988 [2]
Chang, Y. S., The Steepest Descent Gravitational Method for Linear Programming,
Discrete Applied Mathematics 25, (1989) 211-239 [3]
Garvin, W. W., Introduction to Linear Programming, Mc Graw-Hill Book Company, Inc,
1960 [4] Karcicka,
L. D., Teorija i metodi na linearnoto
programirane, Univerzitet ”Kiril i Metodij”,
Skopje, 1987 [5]
Zlobec, S., Petric, J., Nelinearno programiranje, Naucna knjiga, Beograd, 1989 [6]
Vujcic, V., Asic;, M., Milicic, N., Matematicko
programiranje, Matematicki institut, Beograd, Savremena racunska
tehnika i njena primena, Knjiga 7, 1980
|