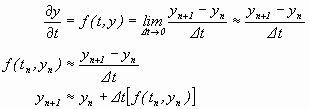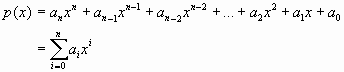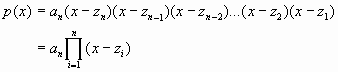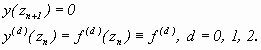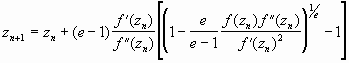|
Newton, Chebyshev, and Halley Basins of Attraction;
Bart D. Stewart
ab8146@exmail.usma.army.mil Real world phenomena commonly exhibit nonlinear relationships, complex geometry, and intricate processes. Analytic or exact solution methods only address a minor class of such phenomena. Consequently, numerical approximation methods, such as root-finding methods, can be used. These root-finding methods include Newton-Raphson, Chebyshev, and helley’s methods. The goal is to gain a qualitative appreciation on how various root-finding methods address many prevailing real-world concerns. The concerns include, how are suitable approximation methods determined; when do root finding methods converge; and how long for convergence? Answers to the questions were gained through examining the basins of attraction of the root-finding methods. Different methods generate different basins of attraction. In the end, each method appears to have its own advantages and disadvantages. BACKGROUND Root finding methods have been of interest for a long time. Why? Often people ask qualitative questions about real-world phenomena, and they want these questions answered. To come to an answer, one must accurately model the real world phenomena in a mathematical model, and then solve the model. In many applications, the solution involves finding a root. Constructing models is rarely a simple process. Models come in many shapes and sizes. Some of these represent a dynamical process – a recipe for how real-world phenomena interact and change over time. How these interactions and changes occur governs the choice of model. For example, the continuous model leading to a differential equation is reasonable for certain phenomena, while difference equations in the form of a recurrence relation address phenomena occurring in discrete steps. Solutions, however, are not guaranteed in every instance. When analytical or exact methods are applicable, sometimes formulas for solutions exist. However, these methods are restrictive, often providing insight into the behavior of only a minor class of real world phenomena. Included in this category are models that can be approximated by linear relationships, simple geometry, and low dimensionality. For a great deal of real world phenomena, that is not the norm. Real world phenomena commonly exhibit nonlinear relationships, complex geometry, and intricate processes. Consequently, exact methods can be of limited practical value (Chapra, 1988). MOTIVATION Where analytical or exact methods fail, numerical approximation methods
often succeed. One such approximation method employs difference equations.
When applied to a large though finite number of steps, difference equations
are closely related to the continuous behavior of a differential equation.
In fact, a continuous model, y(t), can be seen as a limit of the
discrete model, yn(tn) (Figure 1.2).
Although the model approaches are different, solution methods for each share common ground. In the continuous model, solution curves may be obtained from the roots of a linear, constant-coefficient differential equation’s characteristic polynomial. In the discrete model, solutions come from the roots of the recurrence relation’s characteristic polynomial. In either case, roots can be real, imaginary, or complex. Consequently, solutions can vary greatly in their dynamical behaviors. Numerical (Root finding) methods, however, serve as the computational tools that unveil the mysteries of such dynamical behavior. Different methods, however, may produce different results from the same initial guess. So things can get really interesting! METHODOLOGY From a mesh of points within the complex plane, Newton-Raphson, Chebyshev, and Halley root-finding methods numerically compute the successive approximations of some nth order complex polynomial’s roots. In order to better grasp the effects, the results are mapped – thus, creating a geometry of basins of attractions which are the set of starting points whose trajectories are asymptotic to a bounded region (Devaney, 1989). The geometrical differences lend to the qualitative difference amongst the root-finding methods.BEHAVIORS OF DYNAMICAL SYSTEMS While the mathematics describing dynamic behavior may be fairly straightforward, interpreting such behavior can be difficult. In order to truly grasp it, one must familiarize oneself with the role of numerical methods and the utility of mapping their geometry. NUMERICAL METHODS ROLE Numerical methods approximate solutions to mathematically expressed
models. When these solutions are obtained from the zeros of some functions,
root-finding methods serve as the tool of choice. These methods are usually
iterative – beginning with an initial starting value and computing successive
approximate solutions using a well-defined recurrence relation (Figure
2.1). Each successive step yields a numerical solution to the recurrence
relation – in essence, generating a sequence of even better approximations.
Hence, the solution process itself is a discrete dynamical system that
generates a sequence of numbers. Each term of the sequence not only signifies
a numerical solution for the nth iterative step, but
also suggests the ultimate behavior of that solution. Determining such
behavior is not always done by simple inspection. Some sequences are obvious;
others are not. Consequently, numbers alone are often not enough.
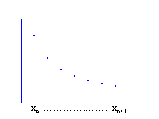
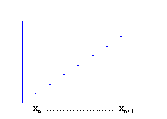
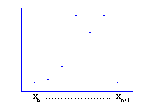
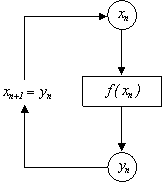
UTILITY OF MAPPING – SINGLE FIXED POINT Another, often preferred, method used to determine dynamical behaviors is to visualize them. Visualization entails mapping out the geometry of the numerical solutions. Why is this geometry important? Simply put, it graphically depicts the dynamical behavior of root-finding methods. As Figure 2.2 suggests, the mapping of a sequence of numerical solutions depicts the behavioral path or trajectory of a single starting point. Starting points that do not change after iteration are called fixed, and qualitative behaviors of other starting points can be interpreted in relation to the fixed points.
Cobweb diagrams help point out the qualitative behaviors near fixed
points using the principle of feedback (Figure 2.3) (after Peitgen, 1992).
The principle of feedback is simple – an input, xn, is
given, processed through some function, f, and then the output,
yn,
becomes the next input, xn+1, repeatedly. When allowing
the ouput to equal the next input, an identity exists so that
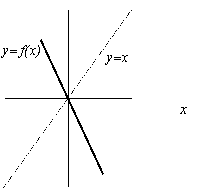
Behaviors about fixed points are converging, diverging or chaotic, and
all can be mapped. Convergent mappings point out attracting fixed points;
divergent mappings denote repulsive ones; and chaotic mappings never settle.
While all three behaviors are essential in describing dynamical behavior,
a simple example excluding chaotic mappings will suffice to illustrate
the point. Consider a simple linear recurrence relation;
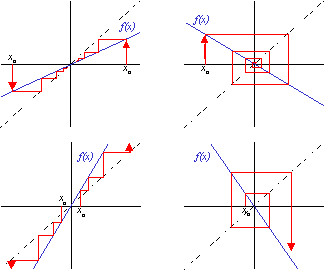
With relatively little effort, the geometrical approach can handle nonlinear
behavior as well. For smooth nonlinear recurrence relations, the same sort
of contracting and expanding argument holds near the fixed point. As Figure
2.5 indicates, the trick is to locally reduce the nonlinear model to linear
parts, apply the graphical analysis, and then couple the pieces together.
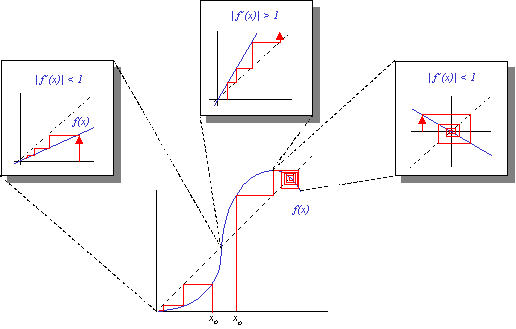
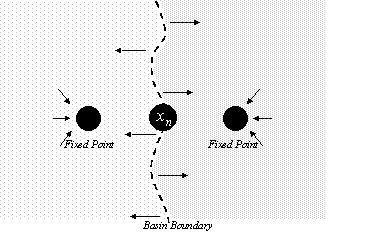
Although dynamic behaviors about a single fixed point are fairly predictable, startling behavioral effects can and often do occur when multiple fixed points exist. UTILITY OF MAPPING – MULTIPLE FIXED POINT When fixed points coexist, the geometry of numerical solutions can change considerably. The effect of each fixed point is no longer simple; rather their effects interact. Consequently, determining such points and their effect is a necessity. Multiple fixed points are often found in the realm of nonlinear phenomena.
While the effect of a single fixed point has been discussed, what happens
when there are two, three, or n of them? How many can there be when
the iterator is a root approximation method? As Figure 2.6 points out,
the fundamental theorem of algebra tells us that an nth
degree polynomial is factorable into n linear factors and contains
exactly n roots, which are not necessarily distinct. Whether these
points are real, imaginary or complex, their coexistence may create surprising
behaviors.
With each additional fixed point, coexisting attractors can exhibit
varying behaviors. Such behaviors are actually emerging in a sort of competitive
state – with each vying to influence a solution’s trajectory. As Figure
2.7 suggests, such behavioral effects may or may not extend globally. Each
attracting region is called a basin of attraction – the set of starting
points whose trajectories are asymptotic to a bounded region. Competition
amongst the fixed points, in the effect upon xn, exists
near and on basin boundaries. Moving the fixed points can create new basins
and destroy old ones.
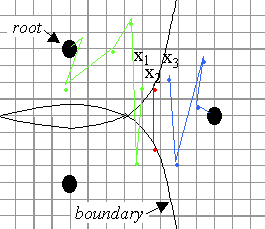
Basin boundaries can take on infinitely many shapes. And basin boundaries
can be far more complicated than a simple curve, and in most instances
are. Within their intricate patterns, commonly referred to as Julia sets,
is the key that reveals some erratic behaviors. Where the basins interact
and compete, the behavior is not so obvious. Figure 2.8 demonstrates how
nearby starting points, which are expected to have similar behaviors, can
assume distinct solution paths, particularly near basin boundaries. Consider
each starting point, x1, x2, and x3.
Despite their ‘nearness’, starting points x1 and x3
reach a root (through different roots) while x2, which
begins on a basin boundary, never settles. Hence, behaviors have a sensitive
dependence on starting points, and can, at times, be considered chaotic.
JULIA SETS Further consideration of such behaviors begins with observing the role
of Julia sets. Julia sets are the boundary of basins of attraction -- distinguishing
which starting points are ‘prisoners’ to some fixed points’ basin, and
others that ‘escape’ them. Consider the following example in Figure 2.9
(after Peitgen, 1992). Note that ‘prisoner’ points converge to some basin,
while ‘escapees’, had any existed, would never settle. While the Julia
set may be quite complicated, its role remains crucial in revealing the
coexistence and competition of complex behavior.
NUMERICAL METHODS Since numerical methods are capable of approximating the zeros of an analytic function, root-finding methods serve as the tool of choice. Such methods come in many shapes and sizes. Some are rather simple; others are complex. Each, however, employs a different iterative approach that affects the geometry of numerical solutions, and thus impacts on dynamical interpretations. Consequently, an investigation of such methods is necessary. Although there are many root-finding methods to choose from, their conceptual origin is the same – that is, all stem from a successive point-wise approximation of an arbitrary function’s root. For example, Taylor’s theorem approximates a function value and, when truncated accordingly, is a numerical method of some sort. Figure 3.1 illustrates another, and more recent, method yielding a one-parameter family, e, of single-point numerical methods capable of finding roots (after Popovski, 1979). Of particular interest were the Newton-Raphson, Chebyshev, and Halley methods. For illustrative purposes, a uniform approach is applied. No matter
the root-finding method, each considers the function, f(z)= z3-1,
and is restricted to real arithmetic for its geometrical interpretation.
From an arbitrary point, xo, approximations are computed
so as to satisfy Popovski’s single-point method,
No matter the function to be approximated, special parameter values,
e,
reveal familiar methods. When e approaches one, the single point
iteration formula reduces to the popular Newton-Raphson method (Figure
3.2). The approximation method simply computes a tangent line to the point
xn
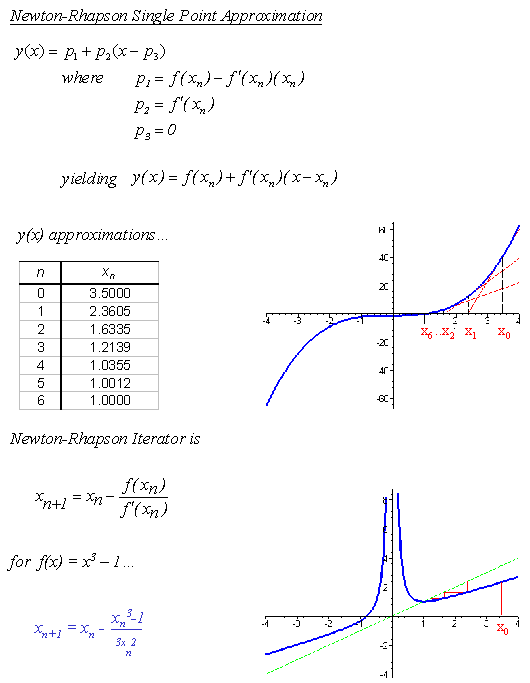
of our function. When e equals one-half, the single point iteration
formula reduces to Chebyshev’s method (Figure 3.3). The approximation method,
rather than line, computes a tangent horizontal parabola to the point xn
of our function. When e equals negative one, the single point iteration
formula reduces to Halley’s method (Figure 3.4). The approximation method
computes a tangent hyperbola to the point xn of our function.
For each of these approximations, the root of its tangent typically represents
a better approximation to our function’s root.
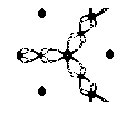
While each method can determine the appropriate root, certain methods are preferred. As Figure 3.6 illustrates, when monotonic behavior exists, the preferential order is clear – Halley, Chebyshev, and then Newton-Raphson. In Halley and Chebyshev, the approximating curves echo the shape of our function. Newton-Raphson’s approximating curve is restricted to a simple line. While in this instance convergence is guaranteed, it varies according to the step sizes of the approximating methods. With the smallest step size, Newton-Raphson is only quadratically convergent while the other methods having larger step sizes are cubically convergent. When a function is not monotonic, the preference is generally uncertain – with no single method consistently better than the others. Clues to determining such an ordering begins with the careful observation of each method’s geometry.numerical Methods’ geometry Again, numerical methods can sort through a dynamical system’s behavior through finding its roots and examining their affect. With different methods yielding different behaviors, an examination of individual numerical methods is necessary. Recall how our three numerical methods, while obtaining the appropriate root, all sought distinct solution paths to it. Consider now a mesh of complex starting points, rather than a single real point, with an assortment of fixed points. What are the numerical solution paths now? What is the effect of the competition and coexistence of fixed points? What numerical method is preferred, if any? Answers to these questions appear when mapping and coloring each numerical method’s solutions. While an nth order complex polynomial with distinct
roots partitions the complex plane into n number of basins, the
partitions may or may not be equally distributed – or even connected for
that matter. In an ideal setting, these attracting regions resemble a Voronoi
diagram – regions containing all points that are the nearest neighbors
to the polynomial’s zero (Figure 4.1). Few things, though, are ideal. Rather,
an attracting region contains all starting points that asymptotically approach
the zero, despite their locality.
One popular method to visualize these regions is basin coloring. The
process simply assigns n colors to the n basins, executes
some numerical method to calculate which initial points within a bounded
region or mesh converge to a particular basin, and paints that basin’s
color to that point (Figure 4.2). Furthermore, the number of iterations
necessary to converge to a root can be shown through variety of color intensities.
Points calling for fewer iterations appear with greater intensity. Through
employing these tools, sensible geometric interpretations are possible
for nearly all complex polynomials.
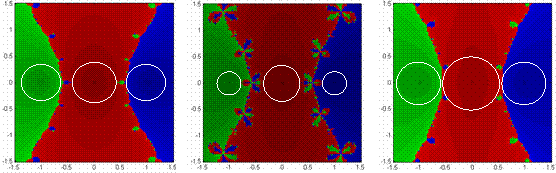
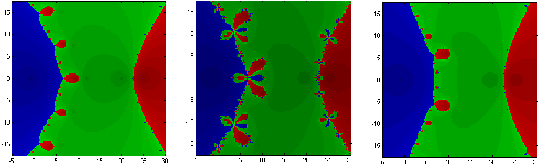
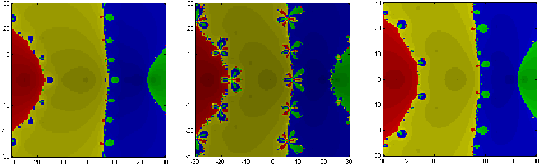
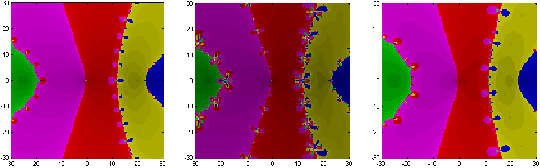
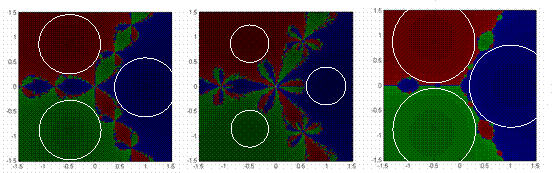
PURE REAL AND PURE IMAGINARY ROOTS When considering pure real or pure imaginary roots, the geometries, while still creating a variety of basin shapes, sizes, and complexities, are remarkably similar – only differing by a rotation to the appropriate coordinate the axes. Consequently, observations for one case support the other. Even in what appears to be the simplest of settings, real roots, our
basins of attraction are not ideal (Figure 4.3). Whether considering the
case of equally or unequally distributed roots (Figures 4.4 & 4.5),
nearest neighbor convergence fails to hold. The shape of the basins roughly
appears to conform to that of a hyperbola. Symmetry is another common factor
that plays a role in shaping the basins. Equally distributed roots generate
symmetry throughout the geometry; unequally distributed roots do not.
With slight exceptions along basin boundaries, the basin sizes for these are fairly comparable. For each, there exists some effective radius of convergence – that is, points in the neighborhood of a root tend toward that particular root (Figure 4.4). As Figures 4.4 suggests, that effective convergence radius not only changes amongst the numerical methods applied, but also with each polynomial considered. With higher order polynomials commonly creating more and more complex geometries, such radii are often greatly reduced. Each method also bears some sensitive dependence on starting conditions.
With nearby starting points assuming distinct solution paths, unpredictable
behaviors can result. Although Figure 2.8 pointed out the concept initially,
chaos’ impact cannot be ignored – particularly with it present in every
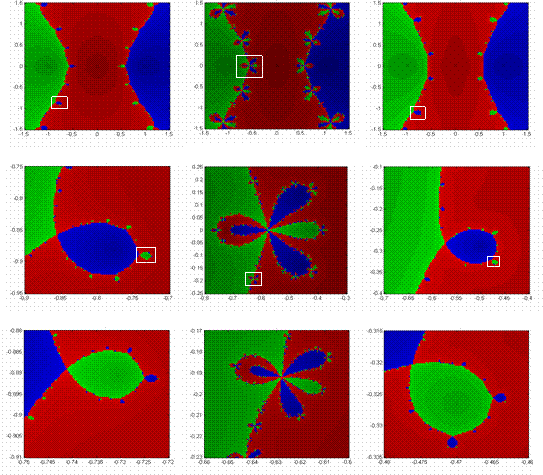
method’s geometry. Figure 4.6 further reveals that basin boundaries may
be self-similar, with infinite levels of detail, characteristic of fractal
geometry.
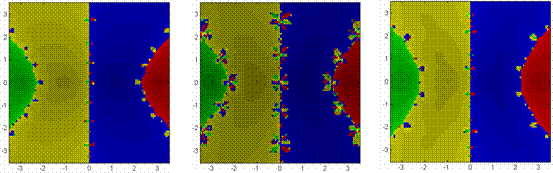
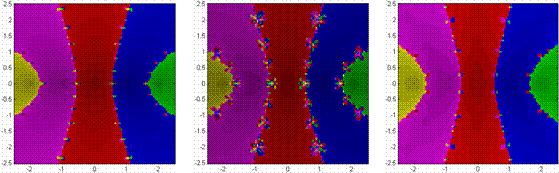
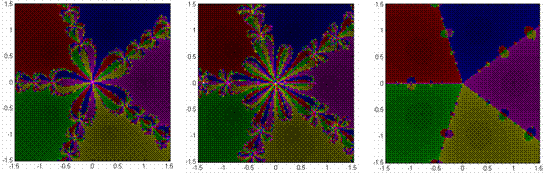
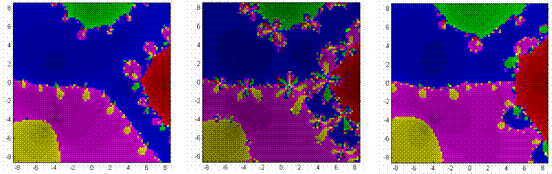
In considering the sensitive dependence on starting conditions, one need to only observe the ‘decorations’ along the basin boundaries for each method’s geometry in terms frequency, size, and structure. As a consequence of the competition and coexistence of more and more fixed points, the decorations appear with greater frequency with higher order polynomials, yet their size decreases. Whether equally or unequally spaced real roots, the Newton-Raphson, Chebyshev and Halley methods appear to experience chaotic dynamics in a phase-shifted manner with each other – an unexpected outcome of their iterators. While pure roots create nifty geometries, things get really interesting with mixed roots. MIXED ROOTS Mixed roots, those roots containing both real and imaginary components, provide a rich variety of basin shapes, sizes, and complexities. In many instances, there are striking similarities amongst these types of roots and pure ones. But when differences appear, a spectrum of spectacular geometries develops. ROOTS OF UNITY (EQUALLY DISTRIBUTED ROOTS) In the simplest of settings, roots of unity, there are more similarities than differences. Nearest neighbor convergence fails to hold. As expected from the equal distribution of roots, basin shapes are symmetric (Figures 4.7). Again, these shapes lend to the equally distributed sizes of each basin. Basin boundaries vary considerably – spanning from the very simple to the exceptionally intricate. Consequently, basins are more disconnected. As for sensitive dependence on starting conditions, the ‘decorations’ for each method’s geometry in terms frequency, size, and structure remains similar to the case of real roots. Furthermore, the effective radius of convergence is also affected accordingly (Figure 4.7). Figures 4.7 & 4.8 suggest, that effective convergence radius not only changes amongst the numerical methods applied, but also with each polynomial considered. Again, as larger order polynomials are considered, basins become more
complicated. Such behavior occurred previously, so this is of no great
surprise.
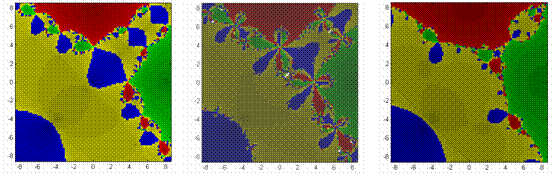
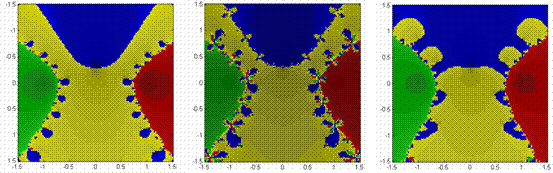
UNEQUALLY DISTRIBUTED ROOTS When roots are positioned irregularly, interesting things can and do happen. In general, the concepts of nearest neighbor convergence failing, basin shape, size, and complexity are as noted previously – but perhaps in a more pronounced fashion. In general, these third order polynomials can produce a variety of familiar behaviors – echoing those previously found with real roots. In certain instances, one is nothing more than a skewed version of the other. When one fixed point is a ‘near-enough’ reflection of another, a ‘near-enough’ symmetric geometry results; otherwise, a distorted geometry develops. Preference for a particular numerical method is subject to the presence of such symmetry. Figure 4.8 reveals how convergence changes with the higher order polynomials – with many containing irregular and unexpected basins shapes and decorations as a result of the competition and coexistence of additional fixed points. Halley’s method generates the most pronounced irregularities, to include distinct breaks in basin connectivity. In all these instances, basin shapes, sizes and complexities vary considerably.
And in nearly every case, the geometry remains unpredictable. But within
this chaotic environment, is there any order?
CONCLUSIONS AND RNDATIONS CONCLUSIONS The Newton-Raphson, Chebyshev, and Halley approximation methods, serve as powerful tools in evaluating complex polynomials’ roots. These different methods, however, can yield different solutions from identical starting points. In determining any preference for the numerical methods, consideration must be given to the polynomial at hand, when do root finding methods converge and how long for convergence. In many instances, the Newton-Raphson and Halley geometries are nearly indistinguishable. When fixed points are a reflection of another, Halley’s method assumes a much larger effective radius over the Newton-Raphson method. Chebyshev’s method, filled with complex boundaries and relatively small effective radii, remains the worst of the three. With the methods relatively comparable in computational speed, the greater emphasis rests in basin shape, size, and complexity. Ultimately though, the method of choice depends on the complex polynomial at hand. RECOMMENDATIONS While room for further research in this topic exists, a particular effort
with respect to more numerical methods, calculating effective radii, and
consideration for repeated roots would prove both challenging and rewarding.
REFERENCES Chapra, S.C. and Canale, R.P., Numerical Methods for Engineers, 2d Ed., McGraw-Hill Book Company, 1988. Devaney, Rober L., An Introduction to Chaotic Dynamical Systems, 2d Ed., Addison-Wesley, 1989. Hansen, E. and Patrick, M., "A Family of Root Finding Methods," Numerische Mathematik, v. 27, pp. 257-269, 10 February 1976. Melman, A., "Geometry and Convergence of Euler’s and Halley’s Methods," SIAM Review, v. 39, pp. 728-735, December 1997. Peitgen, H., Jurgens, H., and Saupe, D., Chaos and Fractals: New Frontiers of Science, Springer, 1992. Pergler, Martin, "Newton's method and Newton basin fractals." [http://www.math.uchicago.edu/~pergler/genteach/newton/newton.html]. November 1999. Popovski, D.B., "A Family of One-Point Iteration Formulae for Finding Roots," International Journal of Computation Mathematics Section B, v. 8 pp. 85-88, July 1979. Press, W.H., and others, Numerical Recipes in C: The Art of Scientific Computing, pp. 279-280, Cambridge University Press, 1988. Smith, Julius O., "The Fundamental Theorem of Algebra." [http://ccrma-www.stanford.edu/~jos/complex/Fundamental_Theorem_Algebra.html]. April 2001. Strogatz, Steven H., Nonlinear Dynamics and Chaos, Perseus Books,
1994.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||