|
CRYSTALLOGRAPHIC GROUPS Raymond F. Tennant Zayed University PO Box 4783, Abu Dhabi, United Arab Emirates
An isometry is any mapping, f : E2®E2, of the Euclidean plane, E2, onto itself which preserves all distances. There are four types of isometries of the plane, rotations, reflections, translations, and glide reflections. In describing symmetry groups of finite patterns, only rotations and reflections are needed. For describing infinite patterns of the plane, all four isometries may be needed. The discrete symmetry groups of the plane, which contain translations in nonparallel directions, are called 2-dimensional crystallographic groups or simply wallpaper groups. Patterns of these seventeen groups are shown in Table 1. Table 1. Two-Dimensional Crystallographic Groups in Traditional Japanese Patterns 
Symmetry Groups The elements of a symmetry group G may be written as an ordered pair (n,j) where nÎE2 is a translation vector and j is a linear transformation of E2 which preserves distance. In other words, jÎO(2), the orthogonal group of 2×2 matrices (rotations about the origin and reflections in lines through the origin). This means the symmetry (n,j) maps the point xÎE2 to (n,j)x=n+jx. Group multiplication in G is defined by composition of symmetries so ((n,j).(w,y))x=(n,j).(w+yx)=n+jw+jyx or (n,j).(w,y)=(n+jw,jy). With
this definition of multiplication in the symmetry group, G,
three invariants of the crystallographic group may be defined.
1. The Planar Lattice of G Let
i
denote the identity transformation. Then (s,i).(t,i)=(s+t,i)
and it follows that the set of translation vectors T={tÎE2:
(t,i)ÎG}
forms a normal subgroup of G. This subgroup of translations may
also be thought of as an additive subgroup of points of the plane E2.
This set of points is called the planar lattice.
2. The Point Group of G With
the multiplication, (n,j).(w,y)=(n,j).(w,yx)=n+jw+jyx.
defined on a symmetry group G, the set H={j.(n,j)ÎG
for
some nÎE2}
is a group called the point group of G. In the case of plane symmetry
groups, the point group, H,
is finite and consists of rotations about the origin and reflections in
lines through the origin.
3. The Action of the Point Group H on the Planar Lattice T If tÎT and jÎH then by the multiplication (jt,i)=n+jt-n,jj-1=(n+jt,j).(-j-1n,j-1)=(n,j).(t,i).(n,j)-1. Therefore,
(jt,i)ÎG
and so yiÎT.
The resulting homomorphism j:T®T
is called the action of j
on T. We say, H
acts on T by conjugation.
4. Method to Produce Fundamental Tile Here is a concrete way to view these ideas
in terms of symmetrical patterns in the plane. The Islamic pattern (Figure
1) consists of two types of stars, octagons and hexagons along with
some overlapping knotwork. The figures below show a sequence of steps for
determining a fundamental region, which may be used to generate the full
tiling.
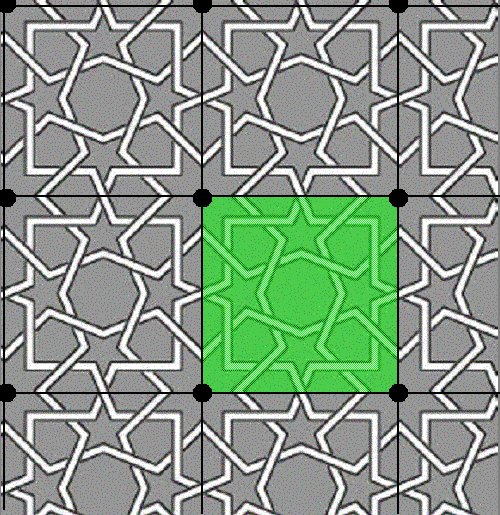
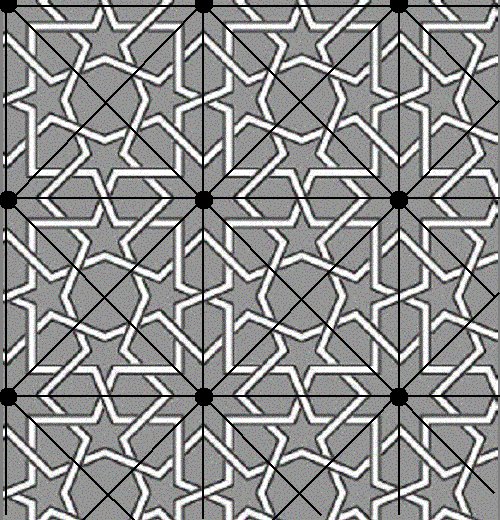
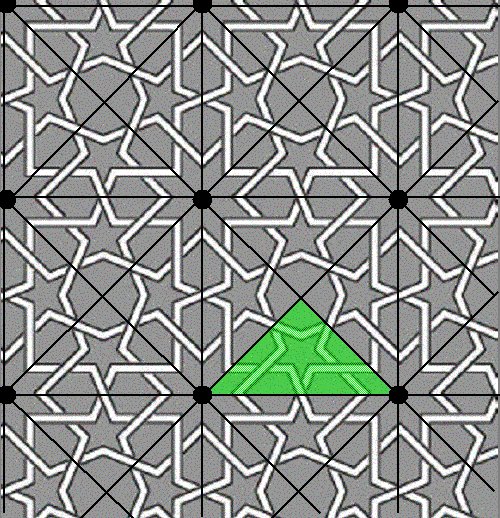
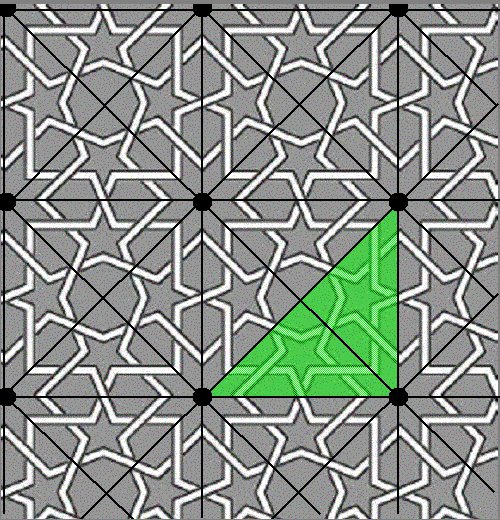
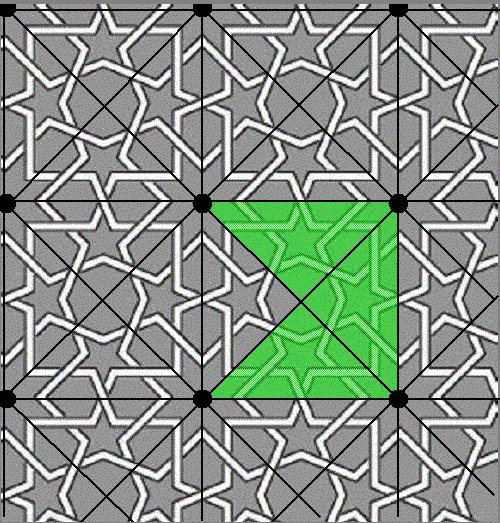
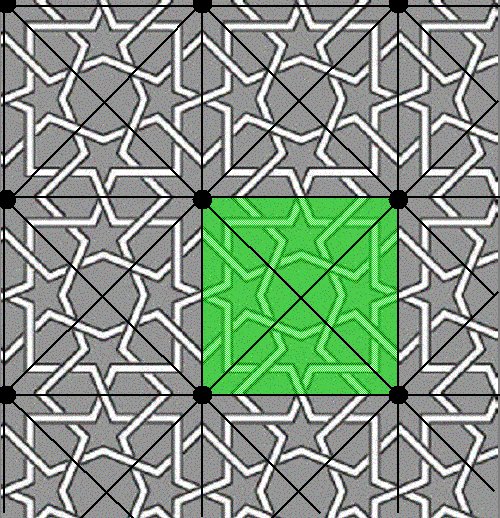
Figure 1. Islamic Tiling First, the tiling is rendered in black, white, and gray (Figure 2). By placing a point at the center of each eight-pointed star (Figure 3), the lattice T is constructed. Note that the lattice is not unique since other points may be chosen but for patterns, which include rotational symmetry, choosing lattice points on centers of rotation may prove useful in determining a fundamental region. Connecting the lattice points with lines of translational symmetry in two linearly independent directions (Figure 4) forms a lattice grid for the pattern. For this tiling, a square formed by this lattice grid (Figure 5) may be used to generate the pattern by translations alone. By determining the symmetry of this square region the point group can be determined. In this example, the region has rotational symmetry of order four. Also, the region cannot be reflected because of the interlocking knotwork so the point group for this pattern is Z4, the cyclic group of order 4, and the crystallographic group is p4. With these symmetries in mind, diagonal lines may be added to the lattice grid (Figure 6) to form a system of congruent isosceles right triangles. One of these triangles serves as a fundamental region (Figure 7) and will generate the entire pattern by rotations. The point group, Z4 , may act on the fundamental region to produce a region which is half of the square (Figure 8), then three-quarters of the square (Figure 9), and finally, the entire square (Figure 10). This square region may then be used to produce the entire pattern by rotations alone or it may produce it by translations as described above. Finally, the Islamic tiling is shown with the fundamental region (Figure 11) that will tile the entire pattern. 
Figure 2. Islamic Tiling - Gray
Figure 3. Lattice Points
Figure 4. Lattice Grids
Figure 5. Square Region that Tiles by Translations
Figure 6. Lattice of Lines with Diagonals
Figure 7. Fundamental Region that Tiles by Rotations
Figure 8. Fundamental Region Rotated by 90 Degrees
Figure 9. Fundamental Region Rotated by 180 Degrees
Figure 10. Fundamental Region Rotated by 270 Degrees
Figure 11. Islamic Tiling With Fundamental Region If the overlapping of the knotwork was ignored, the pattern would have reflective symmetry, the point group would be D4 , the dihedral group with 8 elements, and the fundamental region would be cut in half (Figure 12).
Figure 12. Islamic Tiling With Reflective Symmetry This
method may be generalized to include all the crystallographic groups. In
the crystallographic group p1, all the symmetries are translations
and the point group is trivial. In each of the other crystallographic groups,
there are also symmetries of the form (n,j)
where nÎE2
is a translation vector and j
is a nontrivial orthogonal transformation of E2,
that is, jÎO(2).
These elements, jÎO(2),
are rotations and reflections and make up the point group. The point group
is finite and may contain rotations of order 2, 3, 4, or 6 but no others.
This property is known as the Crystallographic Restriction.
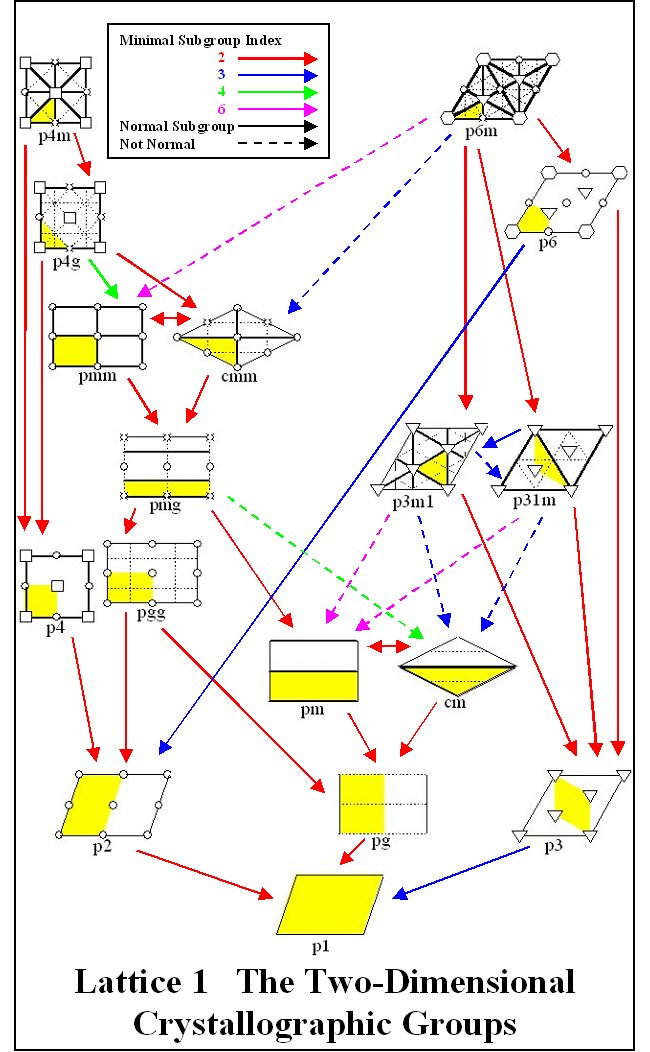
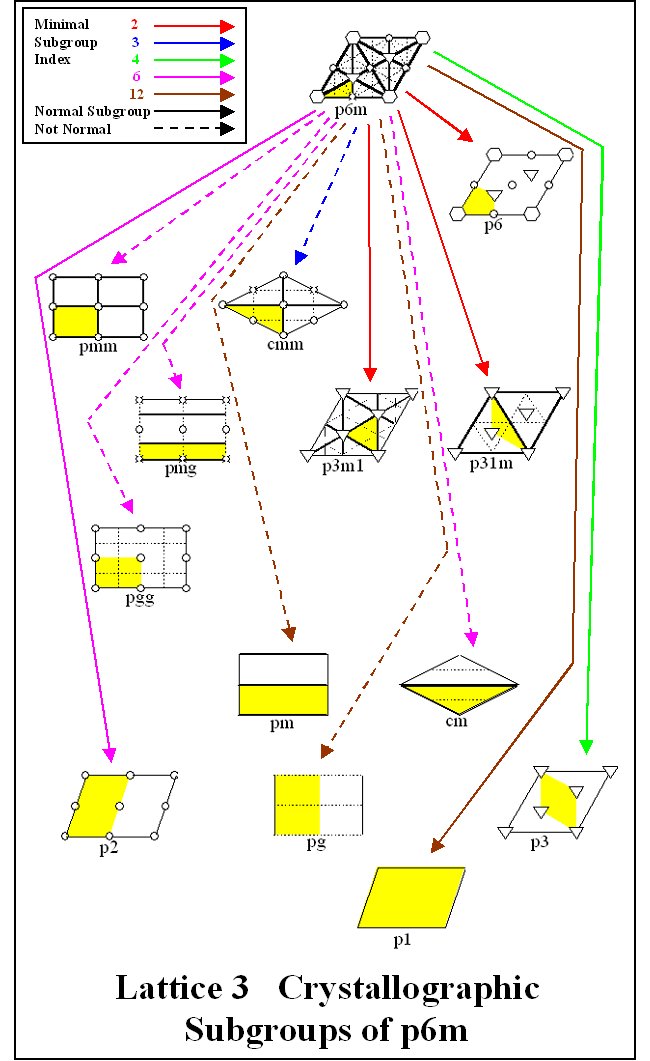
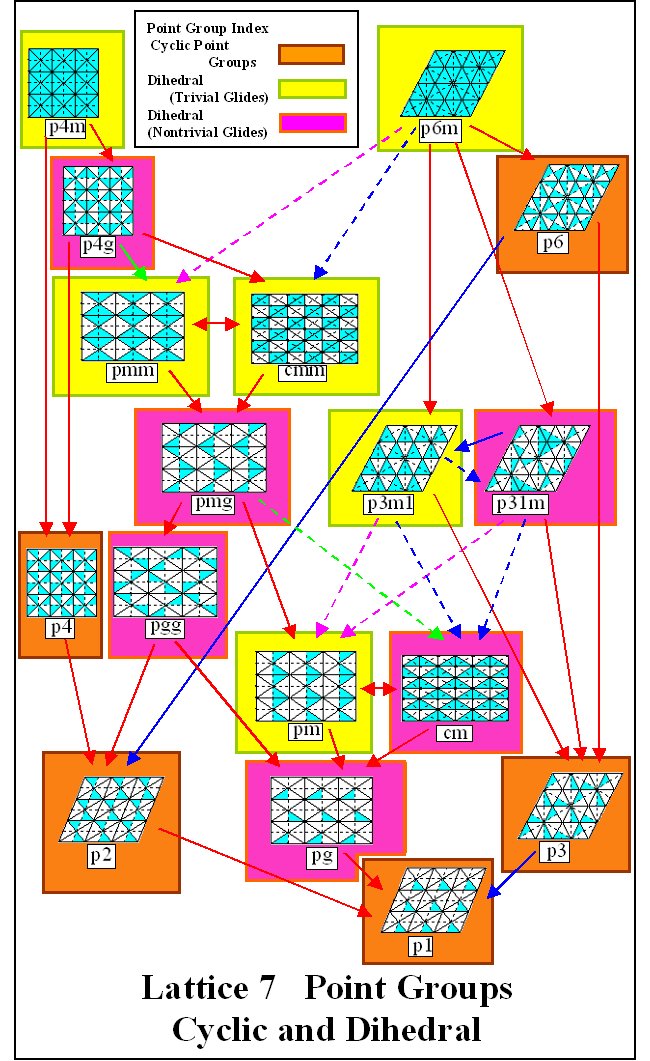
Subgroup Lattices By viewing the seventeen two-dimensional crystallographic groups and patterns all together, connections among the groups may be made. Questions may be answered concerning how the groups sit inside one another as subgroups and how the groups relate in terms of the invariants described above. The subgroup lattices that follow are designed as a tool to illuminate some of these connections. The last three subgroup lattices show techniques involving the removal of symmetry from one crystallographic pattern to produce another. Subgroup Lattice 1 details a subgroup relationship of the crystallographic groups and gives the minimal index in which each group lies as a subgroup of those groups directly above it. Horizontal arrows between two groups denotes the minimal index in which the group on the left lies as a proper subgroup in the group on the right and vice versa. The groups p3m1 and p31m have two lines connecting them since p3m1 is a normal subgroup of index 3 in p31m while p31m is a subgroup of index 3 in p3m1 but it is not a normal subgroup. The symbols used for these subgroup lattices are given in Table 2. Table 2. Symbols for Lattices and Fundamental
Regions of Crystallographic Groups
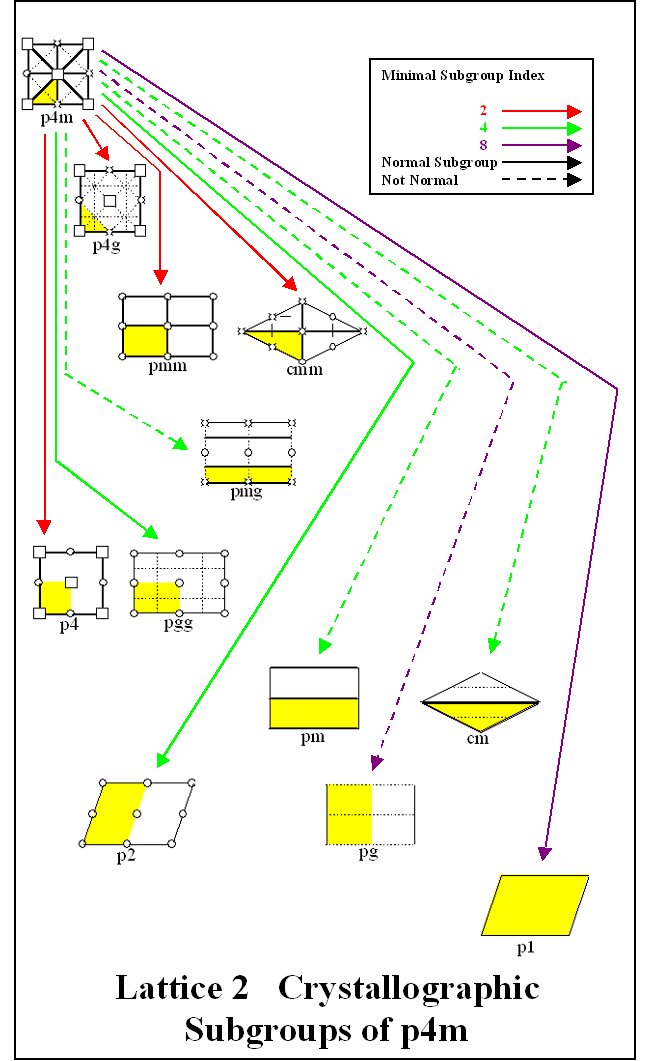
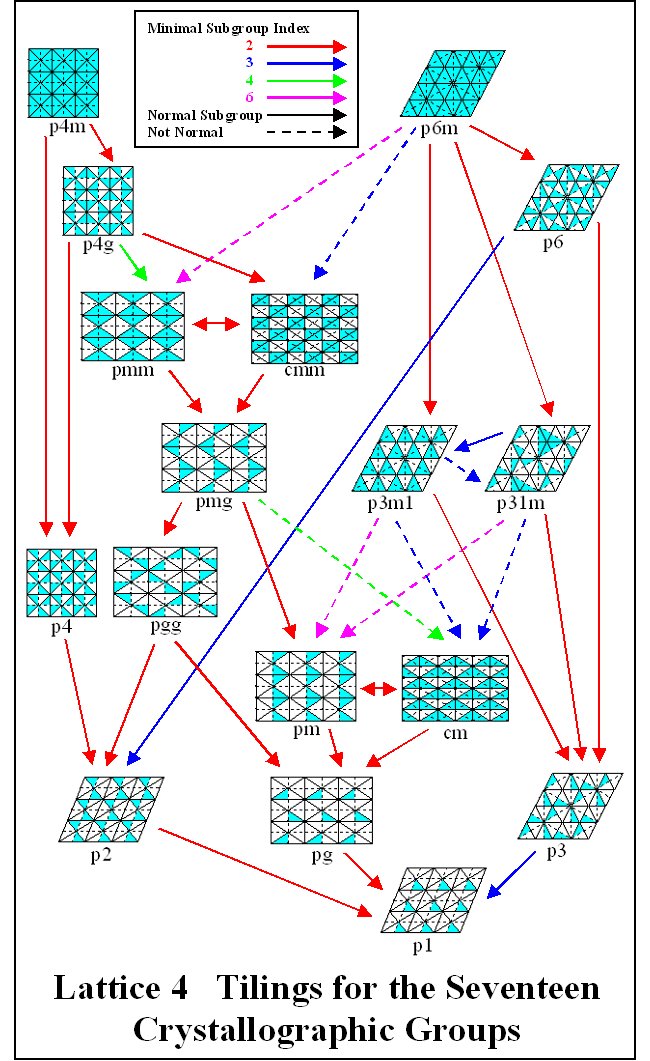
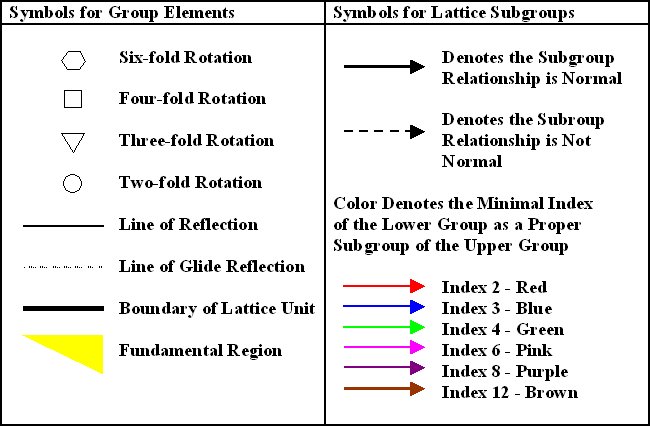 Each of the crystallographic groups is a subgroup of either p4m or p6m or in some cases both. In Lattice 2, all of the crystallographic groups, which lie in p4m along with their minimal indices, are shown. In Lattice 3, the same is done for p6m. Subgroup Lattice 4 gives
a periodic pattern for each of the seventeen groups. Subgroup Lattices
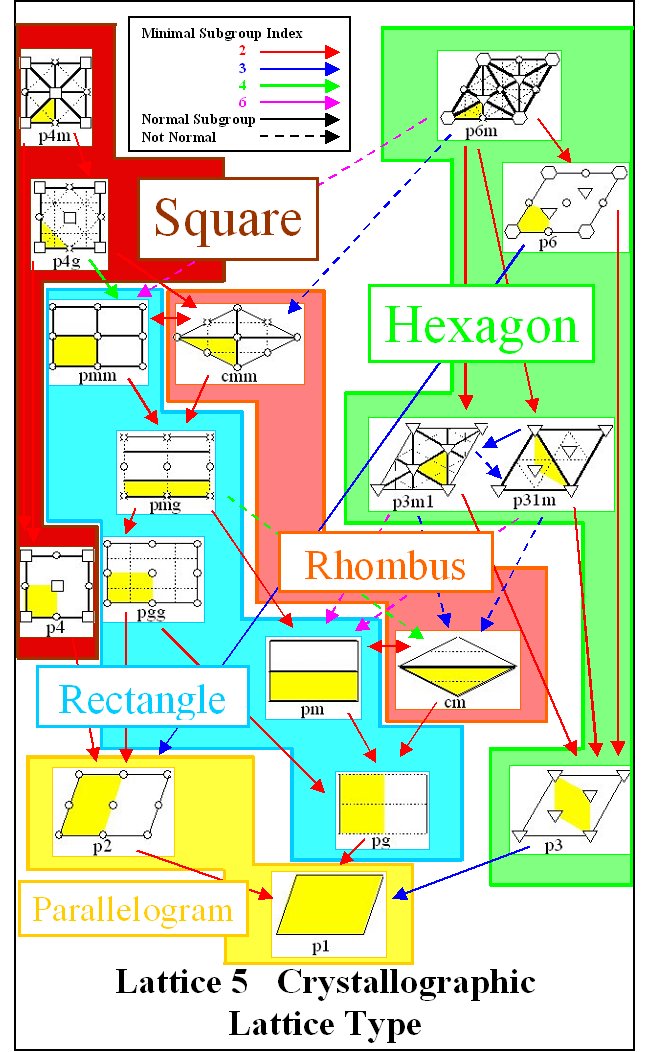
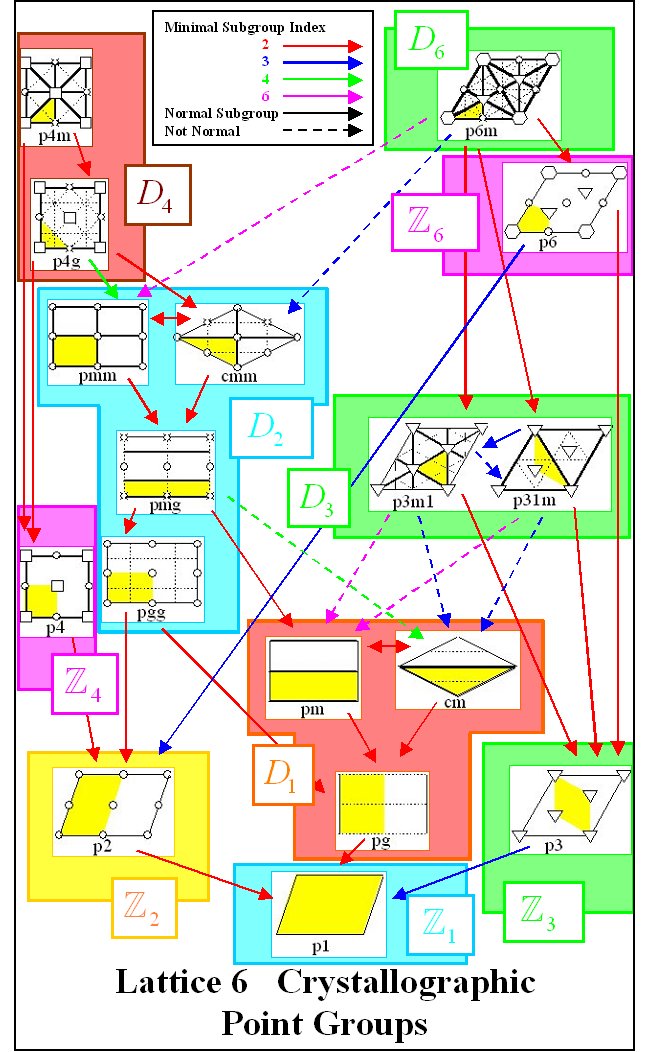
5 and 6 look at crystallographic lattices and point
groups, respectively. Subgroup Lattice 7 categorizes
the crystallographic groups in terms of rotations, reflections and glide
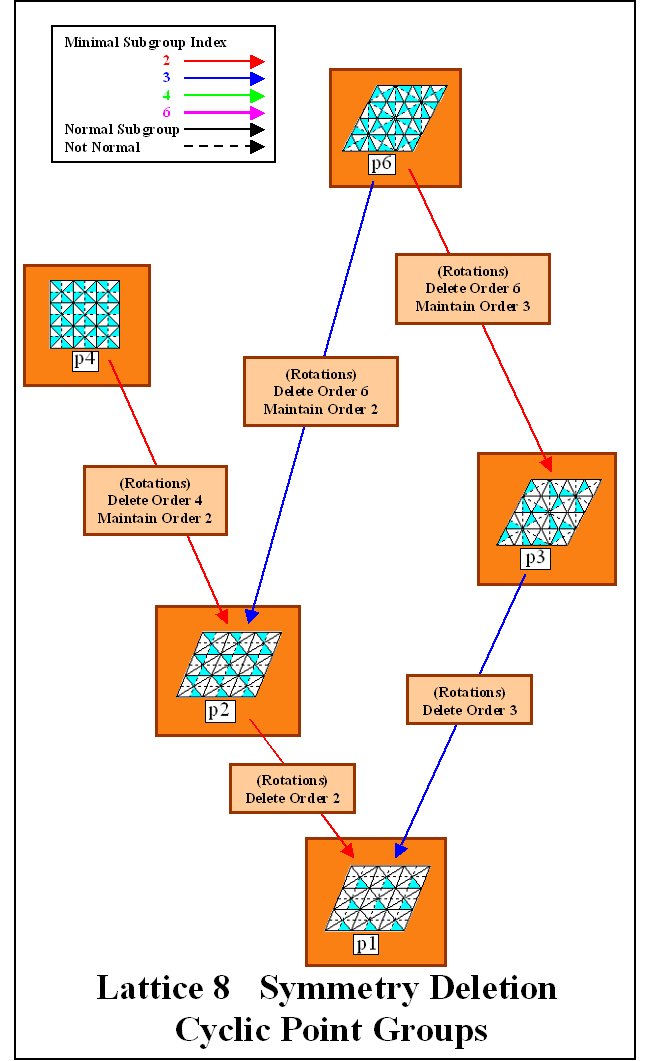
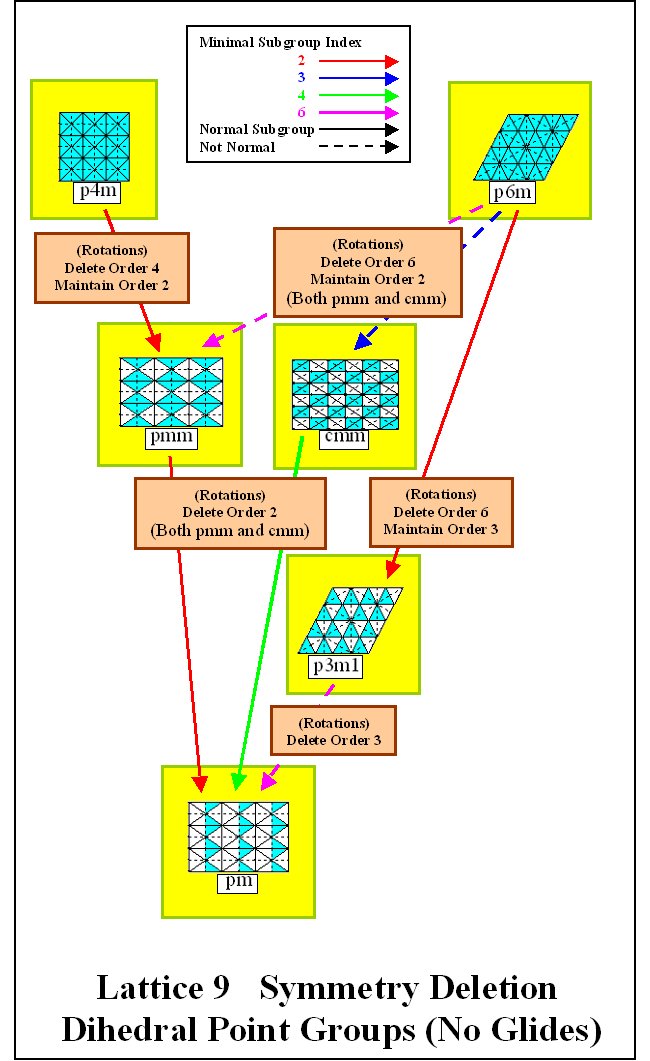
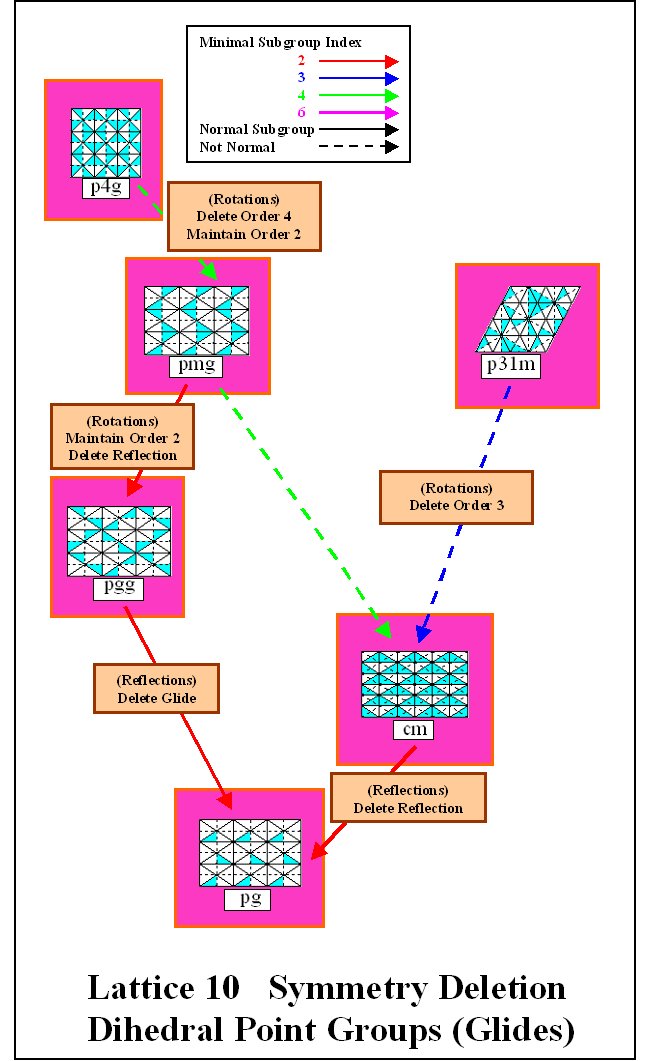
reflections. Subgroup Lattices 8, 9,
and 10 show possible paths to create groups from one
another by deleting symmetry.
References Coxeter, H.S.M (1965)., W. O.Moser, Generators and Relations For Discrete Groups, Springer-Verlag, Berlin, New York, 1965. Jablan, S. (1995), Theory of Symmetry and Ornament, Retieved June 1, 1999 from http://www.emis.de/monographs/jablan/index.html Jablan, S.V. (2002), Symmetry, Ornament and Modularity, World Scientific, Singapore. Mathematics Museum (Japan) (1998), Retrieved
August 15, 2002 from
Schattschneider, D. (1978), The Plane
Symmetry Groups: Their Recognition and Notation, American Mathematical
Monthly, 85, 439 - 450.
|