|
INTERDISCIPLINARY TEACHING STRATEGIES IN THE WORLD
OF HUMANISTIC MATHEMATICS
Raymond F. Tennant Zayed University PO Box 4783, Abu Dhabi, United Arab Emirates
Introduction In his wonderful book, A Mathematician’s Apology, G. H. Hardy compares mathematics to painting and poetry. He writes, "The mathematician's patterns, like the painter's or the poet's, must be beautiful; the ideas, like the colours or the words, must fit together in a harmonious way. Beauty is the first test…." Humanistic mathematics is a philosophy of teaching and learning which attempts to explore the human side of mathematical thought and to guide students to discover this beauty of mathematics. A major goal of humanistic mathematics education is for students to gain an appreciation for mathematics as a creative, collaborative, and exciting endeavor and to move away from thinking of mathematics as a monotonous set of rules used to solve tedious exercises which seem to have no useful purpose. In more advanced mathematics, the techniques of humanistic mathematics are useful in gaining insight into abstract topics. Several teaching strategies of humanistic mathematics
involve interdisciplinary connections between mathematics and other worlds
of thought and methods of learning. This paper focuses on two specific
humanistic approaches for helping in the understanding of mathematical
ideas. The first strategy looks at ways that visual imagery may be used
to illuminate abstract concepts and to make them more concrete. The second
strategy focuses on an example of historical perspective with the goal
to enliven enthusiasm in the manner in which mathematics is developed.
Visual Imagery as Humanistic Mathematics If you walk into a mathematics classroom for students of any age from kindergarten to graduate school and look at what is written on the blackboard (or whiteboard), chances are that you will see some sort of graphic or sketch to help clarify an idea that is being discussed. The solution to many problems often involves the ability to visualize the situation as a sketch, a three-dimensional model, or a computer image. In fact, many problems could not be solved without some sort of visual intuition. The expression, "I never forget a face", seems to reinforce the notion that our visual sense is indeed a strong tool to help us assimilate information and make sense of the world around us. One of the goals of humanistic mathematics is to develop
in students an appreciation for looking at problems and concepts in different
ways and especially in developing visual techniques for delving deeper
into a particular topic. With this goal in mind, we look at two examples
drawn from university courses. The first example looks at methods for using
polyhedral models to learn about group theory. The second example details
holistic methods for gaining insight into higher dimensional space.
Humanistic Mathematics Example 1 A group is defined as a set with a binary operation, like ordinary addition of integers, which satisfies four axioms. These axioms determine that the group with this operation is closed and associative and that there is an identity element and each group element has an inverse. A formal mathematical definition of a group is described in the following manner. The pair (G,*) consisting of a set G with binary operation * is a group if (G,*) satisfies the following four axioms. i. For all a,bÎG, a*bÎG. (Closure) ii. For all a,b,cÎG, a*(b*c)=(a*b)*c. (Associativity) iii. For all aÎG, there exists an element eÎG, such that e*a=a*e. (Identity) iv. Given aÎG, there exists an element bÎG, such that b*a=e=a*b. (Inverse) It appears from this definition that the concept of a group can be approached in a purely algebraic way. Actually, group theory is a major component of the area of mathematics known as abstract algebra but its historical roots lie in the geometric setting of symmetry groups. For students, the use of polyhedral models combined with the notion of rotation group helps to make the abstract concepts of group theory more easily understood. A rotational symmetry of a polyhedron is a rotation that appears to leave the polyhedron in its original position. For the pyramid with regular pentagon base (Figure 1), a clockwise rotation, r, about the base through an angle of 72º is a rotational symmetry. The remaining clockwise rotations which leave the pyramid unchanged are 2r, 3r, 4r, and 5r = identity, through an angle of 144º, 216º, 288º, and 360º, respectively. If this set of rotations is given the binary operation of composition of functions then this set becomes a group called the rotational symmetry group. It is easy to see that the four group axioms are satisfied. This rotational group of a pyramid with regular pentagon base is called Z5, the cyclic group of order 5. Since we could construct a pyramid with a regular n-sided base for any integer n greater than 2 thus, we could achieve a corresponding cyclic group Zn. A prism is a polyhedron with two regular n-sided polygons joined together by n rectangles, which are perpendicular to the base. For an octagonal prism (Figure 2), the rotational group will contain 8 rotations about the octagonal base and also 8 half-turn rotations about the rectangular sides. These 16 rotations form the dihedral group,D8. Again, since we could construct a prism with a regular n-sided base for any positive integer n greater than 2 then we would have a corresponding dihedral group Dn. Thus far, we have two infinite families of groups determined by polyhedral models, namely, the cyclic groups and the dihedral groups. It turns out that there are only three more groups, which may be viewed as rotations groups of polyhedra. The models for these three groups are the regular tetrahedron (Figure 3), the cube (Figure 4), and the regular dodecahedron (Figure 5). These models determine the permutation groups A4 (even permutations on 4 letters), S4 (permutation group on 4 letters), and A5 (even permutations on 5 letters), respectively. During the 19th Century beginnings of group theory, these three permutation groups were referred to as the tetrahedral, octahedral (dual to cube), and icosahedral (dual to dodecahedron) groups in deference to this connection to a rotation group of a Platonic Solid. 
Figure 1. Pyramid Figure 2. Prism Figure 3. Tetrahedron Figure 4. Cube Figure 5. Dodecahedron Figure 6. Inscribed
These basic polyhedral models are useful to create concrete examples of groups. In addition, by viewing the rotations of the models as group elements, a number of topics in group theory may be motivated in a concrete manner. By focusing on a single rotation, the ideas of order and inverse of an element, as well as identity become clear. By viewing all of the rotations of a model, the idea of group action can be developed by observing how the vertices or some other features of the model are transformed under the rotations. With group action defined, concepts like orbit, stabilizer and order of a group follow. By inscribing a tetrahedron inside a dodecahedron (Figure
6), and considering how the two rotation groups are related to one
another, various subgroup topics may be investigated. This particular model
is useful in describing cosets, normal subgroups, and factor groups as
well as Sylow subgroups.
Humanistic Mathematics Example 2 A useful technique for introducing students to an abstract
idea is to begin with examples in a more concrete familiar setting and
then attempt to make progress to the more abstract idea. The works of art
and computer images below illustrate a sequence of images, which give insight
into dimension. Each picture contains some property for describing a particular
dimension. Since the paintings and sketches may not have been created with
these particular mathematical ideas in mind, it may require some imagination
on the part of the student to see the connection to dimension. The sequence
begins with the lower dimensions and progresses to higher dimensions and
to fractal dimension as well.
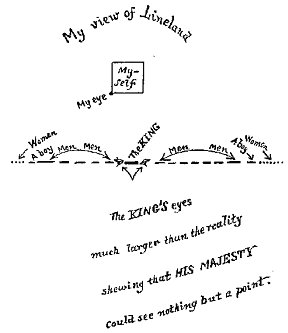
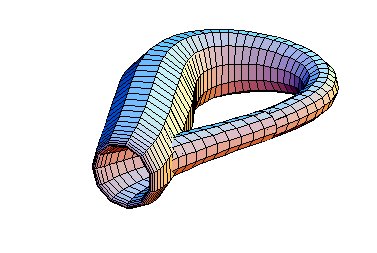
Figure 12. Klein Bottle 4D Figure 13. Menger Sponge Figure 14. Dali - Topology When introducing students to dimension, a good place to begin is with the 1884 satire, Flatland, by Edwin Abbott. This fictitious world of two dimensions helps to give students a glimpse into a world consisting of beings that have length and width but no height. The hero in Flatland, A Square, visits a world of one dimension called Lineland (Figure 7), an even simpler world of inhabitants who live on a line. The 11th Century Bayeaux Tapestry (Figure 8), which describes the events around the Battle of Hastings shows the two dimensional style of artistic perspective where figures were drawn without any depth. Our own world of three dimensions can be described with perspective photography with vanishing points as in a photo of Abu Dhabi (Figure 9). Many people think of the fourth dimension as time but to understand a fourth spatial dimension takes imagination. Pablo Picasso’s, Portrait of Dora Maar (Figure 10) may be interpreted as how a four dimensional being might be capable of seeing all sides of a three dimensional object at the same time. A four dimensional polytope (Figure 11) describes how an ordinary cube may be transformed through another dimension to create a hypercube. The Klein Bottle (Figure 12) is an interesting surface with no inside or outside. The actual surface is a four dimensional object where the neck would not intersect the surface of the bottle. This rendering of the Klein Bottle is done in three dimensions with the Mathematica program. A discussion of dimension might continue with a look at fractals whose dimensions fall between the integers. The Menger Sponge (Figure 13) is formed by removing cubes from the original cube in an iterative manner. This fractal has dimension d=log20/log5»2.7268 placing it a space between two and three dimensions. Higher dimensional surfaces may be described with the ideas of topology. The detail (Figure 14) from Salvadore Dali’s, Persistence of Memory, may be useful for introducing the concept of homeomorphism. The clock melts in a fluid fashion analogous to a continuous topological map. Historical Perspective as Humanistic Mathematics A useful tool for teaching mathematics lies in connecting the students with the history in which the mathematical discoveries were made. This connection is particularly powerful if the teacher is able to make a connection to the cultural heritage of the students. For teachers and students in the Middle East, there is a wealth of historical documents, which help to bring mathematical ideas to life. From the 9th Century AD until the 15th Century AD, the Islamic world experienced a Golden Age of scientific discovery. While Europe was living through the intellectual drought of the Middle Ages, the Islamic world was experiencing a Renaissance of scientific discovery. It was during this period that much of the mathematics of the ancient Greeks was preserved and expanded upon by brilliant mathematicians, astronomers and scientists from throughout the Islamic world. The following example illustrates how historical perspective may be a useful tool in gaining a deeper understanding of mathematical ideas. Humanistic Mathematics Example 3 Having students solve problems from the history of mathematics with the aid of modern day computer technology and animations is an interesting way to introduce students to the history of mathematics while at the same time showing them the problem solving capabilities of the technology of today. Nasir al-Din al-Tusi (1201 – 1274 CE) was one of the greatest mathematicians of his time. This Islamic mathematician wrote a variety of treatises on subjects ranging from Algebra and Trigonometry to Geometry and Logic. The page (Figure 15) is taken from one of al-Tusi’s manuscripts on the Geometry of Euclid and contains a proof of the Pythagorean Theorem. This proof, complete with diagram, shows a variation of an ancient Greek proof by Euclid. From the diagram alone, one can deduce that this manuscript is describing the Pythagorean Theorem, which states, "For any right triangle, the square on the hypotenuse is equal to the sum of the squares on the other two sides." Animation programs are capable of taking this diagram, often referred to as the Bride’s Chair, and bringing it to life by transforming the two smaller squares to perfectly fit into the larger one. 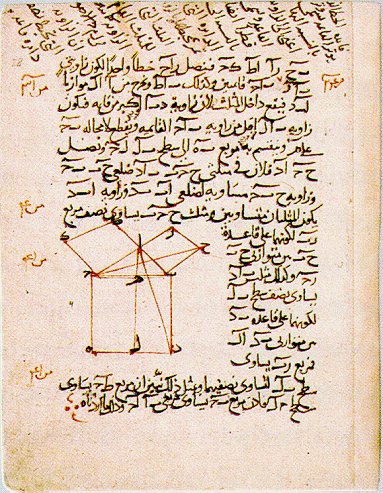
Figure 15. A Proof from Euclid
Figure 16. Al-Tusi’s Description of the "Tusi Couple" One of al-Tusi’s greatest achievements was an improvement
to Ptolemy’s planetary system, which was achieved by resolving linear motion
into the sum of two circular motions in what has come to be known as the
Tusi-couple.
The Tusi-couple may have been used by Copernicus in the 16th
Century in developing his theory of planetary motion. The page (Figure
16) from a 13th Century treatise by al-Tusi describes the
reasoning behind the Tusi-couple. Animations with the computer algebra
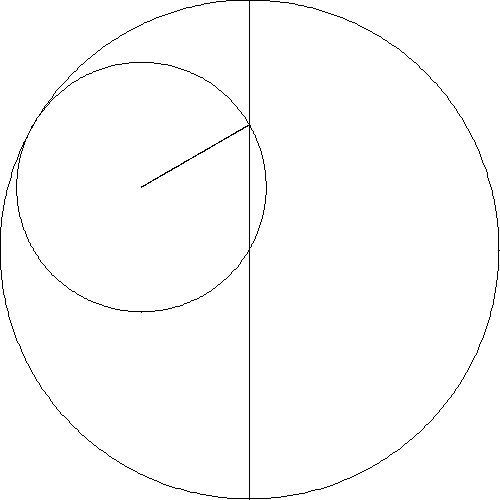
system, Mathematica, can lead students to al-Tusi’s result. An interesting
experiment is to investigate what designs result as a point on a smaller
circle is followed as it rolls around inside a larger circle. The final
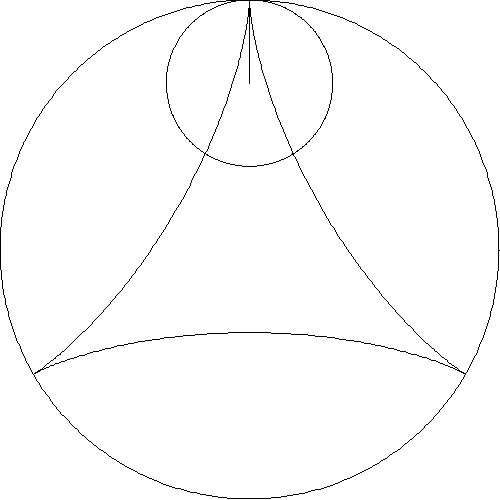
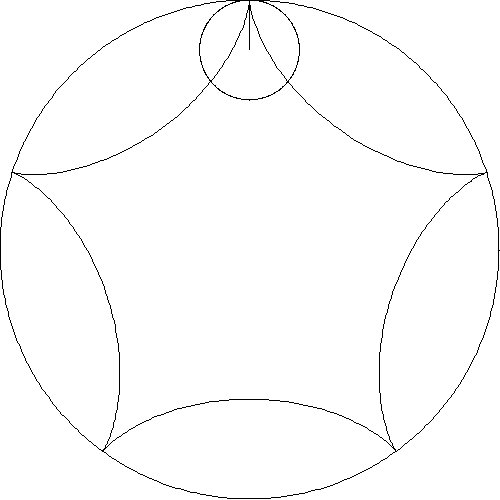
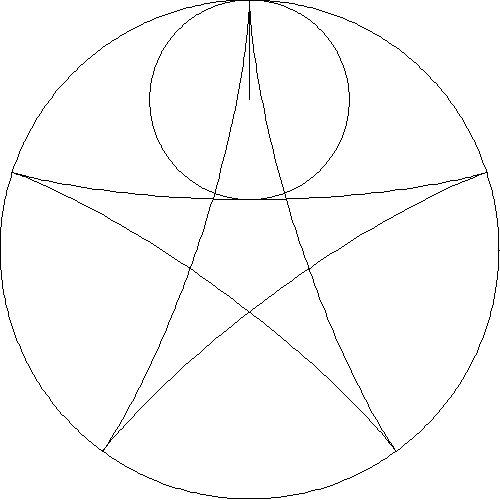
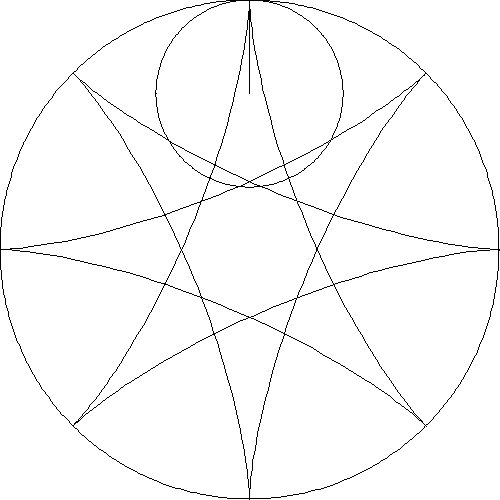
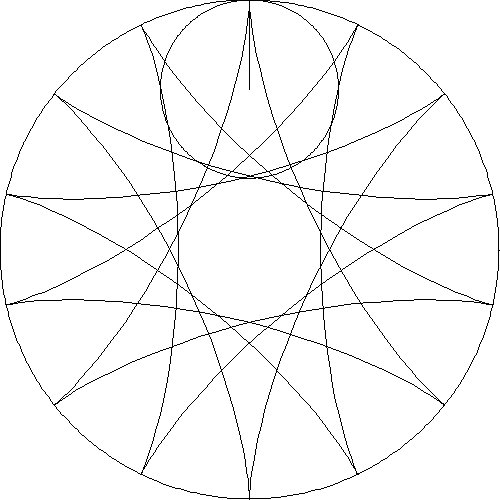
designs from several animations are shown in Table 1.
The first row shows results when circles of varying radii are rolled inside
a fixed circle. The second row shows five slides of an animation when the
radius of the smaller circle is one-half the radius of the larger circle
These five patterns duplicate the diagrams in al-Tusi’s 13th
Century manuscript (Figure 16) and his result of two
circular motions producing linear motion is seen.
Table 1. Patterns – Ratios of Large Radius to Small Radius.
3:1
5:1
5:2
8:3
14:5
2:1
2:1
2:1
2:1
2:1
Conclusion Humanistic mathematics is a philosophy of teaching mathematics,
which guides students through mathematical ideas by the use of imagery,
history, as well as other interdisciplinary connections. It may also involve
innovative classroom strategies involving collaborative groups, the Internet,
and teaching techniques that pique student interest and clarify mathematical
ideas. At its very best, humanistic mathematics creates a learning environment
that is productive, meaningful, and enjoyable for students.
References Abbott, Edwin (1884), Flatland: A Romance In Many Dimensions, Dover Publications. Gallian, Joseph (1998), Contemporary Abstract Algebra, 4th edition, Houghton Mifflin, Co. Kaku, Michio (1995), Hyperspace: A Scientific Odyssey Through Parallel Universes, Time Warps, and the Tenth Dimension, Alfred A. Knopf Co. Saliba, George (1999), Whose Science is Arabic Science
in Renaissance Europe?, Retrieved March 15, 2002 from http://www.columbia.edu/~gas1/project/visions/case1/sci.1.html.
|