| Following Euclid’s “rule”, the golden number
(or golden section, mean, or ratio, or divine proportion, etc.) arises
“when a line segment of length x (>1) is divided into two pieces of
lengths 1 and x-1, such that the whole length is to 1, as 1 is to
the remaining piece, x-1”. This produces the equation x2
- x -1 = 0, of which f =
(1+√5)/2» 1.618… is
the positive solution. Note that f2
- f -1 = 0 implies
f-1=
1/f
» 0.618…, which is a
solution of x2 + x - 1 = 0. Recent discoveries of
a pentagonal structure in quasi-crystals and DNA-structure, justified the
introduction of a “golden angle” of 36°, as sin(2×36°)/sin(36°)=f.
While the pentagonal property may be the reason for the occurrence of the
golden number in elementary geometry, population growth models may appeal
on the number since f2
= f +1, implying that the
arithmetical progression 1, f,
1+f, ... is a
geometrical one as well. Furthermore, the ratio is
f, and since the proportion
of consecutive Fibonacci terms 1, 1, 2, 3, 5, 8, … tends to
f as well, the occurrence of
f in many unpretentious
proportions of 2 to 3, 3 to 5 etcetera is not surprising. Nevertheless,
when the context is different from artistic proportions or population
growth, f's apparition may
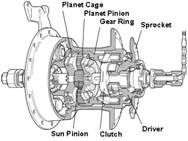
still come as a surprise. For instance, when gears allow to reach the
consecutive speeds v1, v2, v3,
… it seems natural to require that this increase in velocity uses the same
proportion, while technical cog wheels constructions may lead to an
addition property of these speeds (see, Huylebrouck, 2002). Thus, the v1,
v2, v3, … should be arithmetical and
geometrical, that is, v2 =
fv1, and v3
= fv2 =
v1 + v2 (see Fig. 1).
|
|
|
|
 |
| Fig. 1 : A cogwheel for adding golden gears, and the Euclidian line segment subdivision. |
|