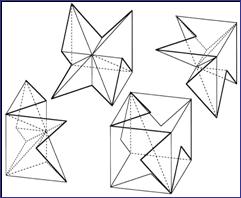
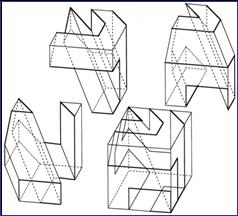
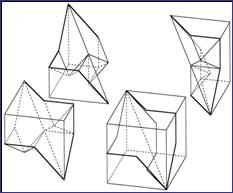
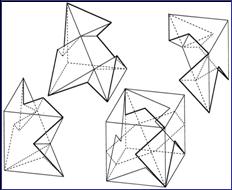
•  Puckered Trisection: This was the first and (to date) the most thoroughly examined of the trisection types—and it tended to prejudice the discovery of other types. Determining the interior faces of the trisected pieces can involve a point of resolution, located along one of the cube’s (four) diagonal threefold axes—such an axis being the one feature common to all trisected pieces. This point enables the triangulation of all interior faces. In the early phase of the study of this type, the cut lines—prominent feathers which a cube exteriorizes when trisected—were termed traceries. Each trisected cube has three tracery lines, which run in a threefold arrangement from one of the polar extremes of the cube’s diagonal axes (the one activated in this instance) to the antipodal extreme of that diagonal. (The term puckered is borrowed from chemistry.)

•  Multiple Points of Resolution Trisection—variant of the Puckered Trisection: It was eventually realized that numerous points of resolution (PR) could be located along the so activated diagonal axis—up to a number (pn) that is relative to the number of line segments (LS) of a tracery. (LS – 2 = pnPR)

•  Scoop and Mound—variant of the Puckered Trisection and of other types: A volume can be extracted from the whole or from a part of one interior face of a trisection and mounted symmetrically on that face’s correlative, mirror-opposite face. (The Scoop and Mound would not have to be executed within the boundaries of a single face—but it could not interrupt the diagonal axis.)

•  Extreme Extensions of Scoop and Mound: Cavities that Penetrate the Cube’s Exterior Faces—variant of the Puckered Trisection and of other types.

•  Pyramidal or Radiant Trisection: When the single point of resolution is slipped to the extreme—to a polar extreme of the cube’s activated diagonal axes—all lines of resolution emanate from that point.

•  Snub-pyramidal or Snub-radiant Trisection— variant of the preceding: By shaving the three faces that adjoin the radiating point of resolution, complex tracery lines will appear on these three faces.

•  Extruded or Prismatic Trisection: All lines of resolution, internal to the cube, are parallel. Complex tracery lines can lock a Puckered Trisection so that it cannot be separated and/or assembled, unless the trisected pieces are rubbery; but in an Extruded Trisection, very complex traceries can be delineated (threefold-symmetrically) on the three faces of a cube that encircle one of polar vertices—beginning at a polar vertex of the cube and ending at one of the cube’s six equatorial edges. The consequent traceries, projected onto the opposing three mirror-rotated faces, will be even more complex. An example of this type was produced in 1971 (by Lawrence Tan), long before the distinctive properties of this trisection type were recognized.

•  Equatorially Cut Trisection: With respect to any one of the cube’s four volumetric, diagonal axes, a perpendicular, equatorial cut will bisect a cube, such that the plane of bisection is a hexagon; each bisected part is left with improper threefold rotation and can, therefore, be sectioned accordingly into three congruent pieces in respect to its threefold axis. Then a trisected piece of the one bisected part can be attached to a trisected piece of the other bisected part, face to face in respect to the exposed equatorial plane and to the cube’s threefold diagonal axes. Note: the equatorial plane can be deformed in accordance with the equatorial edges of the cube, thus widening the possibilities of this type.

• Latitudinally Cut Trisection—variant of preceding: Positioned parallel to the hexagonal equatorial plane, which itself does not have to be cut, any number of latitudinal cuts can be made. Each latitudinal layer can then be trisected and a qualified trisection of the original cube can be assembled in the same manner in which the Equatorial Cut type is assembled. An example of this type was produced in 1978 (by Daniel Baccari), but the properties of this type escaped (indeed, frustrated) identification for a number of years afterwards. Note: the planes cut parallel to the equatorial plane can be deformed in accordance with the equatorial edges of the cube, thus widening the possibilities of this type.

•  Twistruded or Helical Trisection: In what might be considered a special case of the Latitudinally Trisection, infinitely thin latitudinal cuts can be made; each layer is then trisected so that the cuts advance by a constant number of degrees from the preceding cut and assembled accordingly This produces triple interlocking helices, which will screw together and apart. In the consideration of da Vinci’s double helical staircase for Chambord, it was realized that a triple helix would be a possible solution to the trisecting of the cube.

•  Cubing the Cube and Trisecting Each Cube along the Common Axis Trisection: It was not until March 2004 that this type was identified, while a cube that was made up of 4 x 4 x 4 (or 64) cubes was being analyzed—after which a number of trisected solutions, made up of 2 x 2 x 2 (or 8 cubes), were reassigned from the Puckered category to this category. Due to the newness of this realization, this type has not yet been well examined.

•  Hybrid or Pedestaled Trisection: A trisection can be mounted on a base which is the bottom portion of a yangma (Gardner 1980)—the most basic trisection, so named by the Chinese who identified it in ancient times—that is, a cut that is made thorough the yangma, parallel to the yangma’s whole square face. This type of trisection was identified in a (now anonymous) earlier student’s submission only in August 2004. This is also in need of further examination.