|
In the third stage, by applying the previously
developed method a process of the actual identification of the self-dual
spaces was carried out. Finding the 2-fold networks is supposed to be exhausted at this stage. The method of locating the 2-fold networks is based on identifying the E.P.R.s that may, as stated above, contain 2-fold axis that rotates them into themselves. It is not a combinatorial method, and hence we may have missed some of the “2-fold networks” in our search. At this stage fourteen different “2-fold networks” were found. Among those twelve were found to contain seventeen different closed periodic cells that may enclose a periodic unit of a 2-manifold. With regard to the first category, duplicating these closed cells – “the soap membrane networks” – led to the discovery of eight topologically different 2-manifolds so far. Among them, a new, unknown to date, 2-manifold was discovered, which was designated “The Cubic Diamond 2-Manifold.” (Figure 3)
Among the seventeen different closed periodic cells, mentioned above,
there are six closed cells that consist of a “split perimeter”. These
“split perimeters” can enclose a “periodic 2-manifold unit” of the second
category surfaces, i.e. they can enclose in the periodic closed perimeter
cell a successive smooth hyperbolic “periodic 2-manifold unit”, which is
topologically different from the minimal “periodic 2-manifold unit”
previously discovered. Thus a new class of 2-manyfolds, designated “The
Multiple-Sleeved Class” was found (Figure 4). The proposed method of identifying the 2-manifolds that divide between pairs of self-dual networks, led to the discovery of new 2-manifolds in addition to the seven 2-manifolds that two of them were first discovered by Hermann Amandus Schwarz (1843-1921). The 2-manifolds were looked for in representative groups, relating to symmetry groups, the number of which is finite. This does not necessarily mean that the number of 2-manifolds and/or the number of self-dual pairs of networks are also finite.
|
|
|

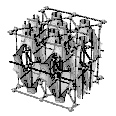 This class contains infinite number of topological different 2-manifolds.
This indicates that the tunnel axes of these 2-manifolds represent pairs
of identical-dual networks that differ from each other.
This class contains infinite number of topological different 2-manifolds.
This indicates that the tunnel axes of these 2-manifolds represent pairs
of identical-dual networks that differ from each other.