|
SYMMETRIC AND NON-SYMMETRIC WAYS
Tomasz Michniowski
1 CURVATURES AND FORCES Relying on what we have told two years ago in Bruxelles let's exclude
the case when the observer travelling through the space-time near to a
pure Ricci-like singularity. Let's now discuss another possible situation,
when a hypothetical observer, walking along on a space-time-like path towards
the singularity's horizon, approaches a Weyl-like or a mixed type singularity.
All well-known physical features of the space-time are almost steady in
areas where the values of separate Weyl tensor's coordinates are small
(and where the changing of them is very slow along each space-time-like
path). They start to change rapidly as the observer approaching the singularity's
horizon. The tensor's coordinates are describing the appropriate space-time's
curvatures, which we usually interpret as gravitational potentials. Gradients
of these potentials are physically equal to the 'gravitational forces',
and in areas, where the Weyl-type curvatures are growing very quickly,
we can observe violent escalation of them. This implies that the observer,
still walking along the space-time path towards the singularity, must suffer
extreme, uncommon physical effects, leading him irrevocably to the state
in which he must "be torn into bits and pieces" by enormous tide forces.
2 DIFFERENT WAYS OF "BEING TORN" Of course, ways of "being torn" are different in respect to the type of the singularity and shape of the space-time-like path the observer walking along. Depending on the type of the singularity, the "torning forces" can be very regular and symmetric, or more chaotic and unforeseen. For example, when observer approaches stationary black hole the "torning forces" can be very regular and symmetric, in result of simultaneous crosswise compression and lengthways stretching of his body.
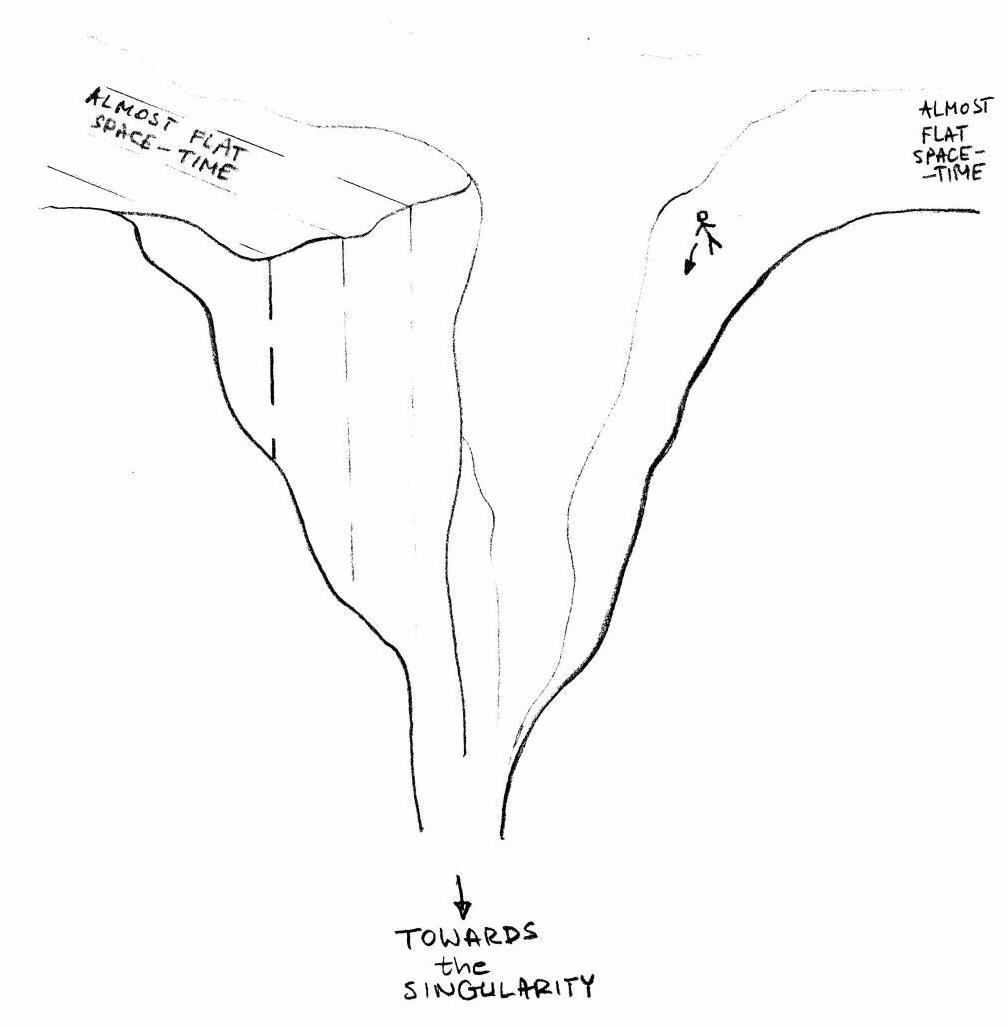
Fig.1 Physical observer approaching singularity of mixed type In case of approaching a singularity of mixed type, the situation will be quite different (Fig.1). Then the observer's body will feel the influence of multidirectional forces of different strength, which effect will create quite unsymmetrical "torning forces". The effect would depend strongly on the path the observer had chosen when approaching the singularity. Especially dangerous and unpleasant for the observer seems to be a case of the singularity of "edge"-type (Fig.2). Now the observer experiences very special, completely unsymmetrical way of "being torn". He simply will be "sliced" when touching the horizon of the "malicious" singularity. What is worse, the observer up to the last moment will not realise any forces or experience any other effects which could warn him of the presence of such topological defect of space-time in his nearest neighbourhood.
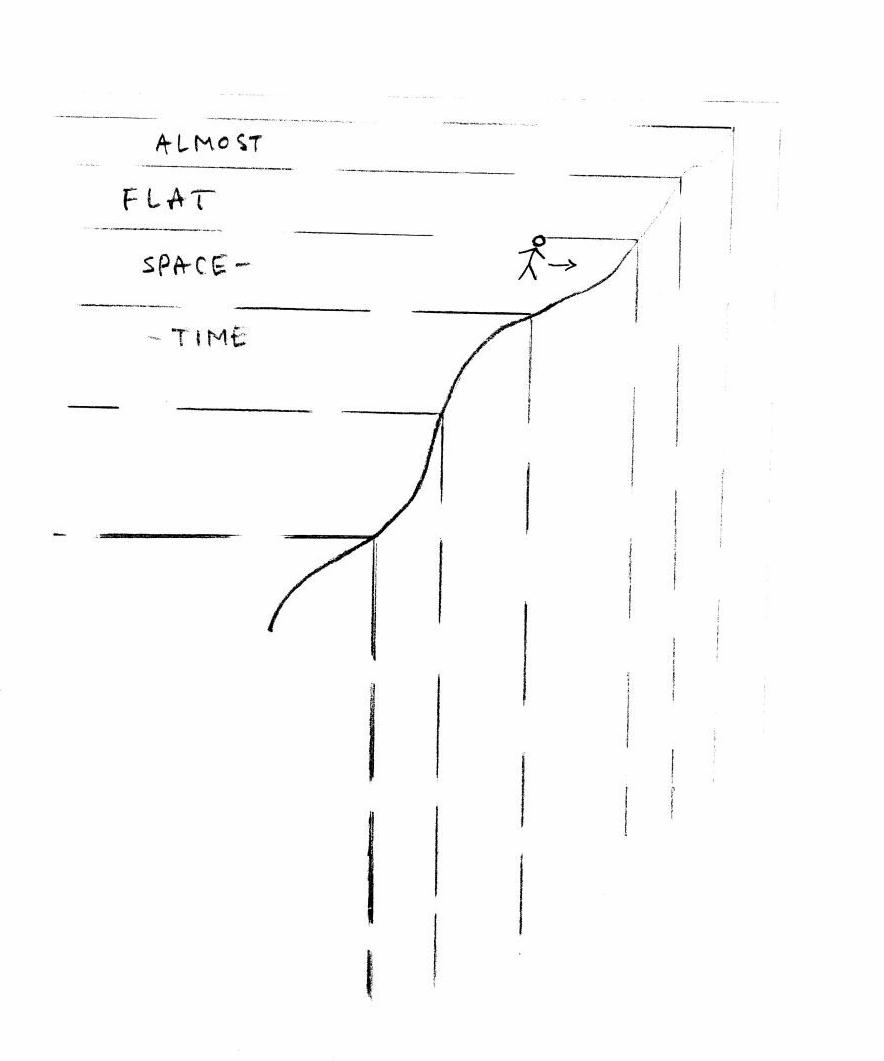
Fig.2 Physical observer approaching the edge of the space-time 3 CONCLUSION Investigating different ways of the "being torn"
phenomena in different areas of topological defects of the space-time,
gives us better knowledge about symmetry (i.e.: physical features, see
[4]) of the space-time itself and about its geometry in general. Specification
of "being torn" phenomena in context of their symmetrical features gives
us comfortable opportunity of creating "maps" of the space-time, where
we could identify singularities of different types (see the general classification
of space-time singularities on Fig. 3) by finding areas of symmetric (or
not symmetric) distributions of space-time-like paths. These results are
valuable both in scientific and in didactic context.
Fig.3 Classification of space-time singularities References Heller, M. (1988) Theoretical Principles of Cosmology, Warszawa: PWN . Heller, M. (1991) Singular Universe, Warszawa:
PWN.
|