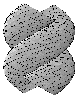SPACE CURVES WITH CONSTANT THICKNESS:
THE CASE OF CIRCULAR HELIX
TOHRU OGAWA
|
Name: Tohru Ogawa, Katachist
and Symmetrist, Physicist, Geometer, Mathematical Scientist, Philosopher
(b. Tokyo, Japan, 1936).
Address:
University of Tsukuba (Emeritus Professor) and NPO-ISTA (Interdisciplinary
Institute of Science, Technology, and Art), 2-106-B-102, Kitahara, Asaka,
Saitama, 351-0036, Japan.
E-mail:
ogawa-t@koalanet.ne.jp
Fields of interest: Mathematical
science mainly geometrical and studies of wide range including culture,
education, society, peace, etc. without any boundary in principle, a kind
of intellectual gourmet.
Awards: Prize for an Excellent
Research Paper (Society for Science on Form, Japan, 1995).
Publications:
Ogawa, T. (1983) Problems in a digital description of
a configuration of atoms and some other geometrical topics in physics,
In: Yonezawa and Ninomiya, eds., Topological Disorder in Condensed Matter,Springer,
60-77; Electronic publication in: Visual Mathematics, Vol.2, No.1.
Ogawa, T. (1985) On the structure of a quasicrystal: Three-dimensional
Penrose transformation, Journal of the Physical Society of Japan,
54, No.9, 3205-3208.
Fujiwara, T. and Ogawa, T., eds. (1990) Quasicrystals,
Heidelberg: Springer.
Ogawa, T. (1994) An Aspect of katachi (~form), In: Takaki,
R., ed., Research of Pattern Formation, Tokyo: KTK Scientific Publisher,
11-22.
Ogawa, T. (1996) Katachi
and symmetry: Towards interdisciplinary and intercultural cooperation,
[Keynote Lecture], In: Ogawa, T., Miura, K., Masunari, T., and Nagy,
D., eds., Katachi U Symmetry, Tokyo: Springer, 7-26.
|
| Abstract:
Aiming
a new type of educational attempt to inspire some developing ideas, the
author enjoys a kind of designs by the tool of 3D graphics of Mathematica
and Maple. He starts the process with giving constant thickness to simple
spatial curves. He himself does calculate and draw graphics but these are
not the main subject at all for students, who should enjoy the interesting
properties, raising some questions and ideas for the next step. He thinks
both of the calculation and graphics work as the next task after the students
feel necessity for that. The main part of the presentation is to show the
interesting properties of the 3D-curves with constant thickness. First
of all, we start with the 2D-correspondence of the problem. The concept
of helical symmetry is defined that is proper to the present problem.
|
1 INTRODUCTION
Nowadays, too many people in Japan regard studying mathematics and physics
as for rote leaning of formula. Most of scientists and mathematicians take
the situation as serious. We should construct more creative education.
It must be changed in order to be more creative one. This work is one of
the attempts to this direction and at the same time, he enjoys by himself
to study and to images the detailed structure of ideal 3D structures.
2 THICKNESS OF A LINE IN 2D and 3D
A line segment is a straight line of finite length 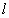 .
It is reasonable to define a line segment with 2-dimensional thickness
or width .
It is reasonable to define a line segment with 2-dimensional thickness
or width 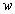 as a rectangle
and the area of a rectangle is width by length as a rectangle
and the area of a rectangle is width by length 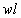 .
Similarly, it is reasonable to define a circumference of radius .
Similarly, it is reasonable to define a circumference of radius 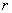 with width
with width 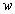 as a pair
of concentric circles whose radii are as a pair
of concentric circles whose radii are 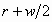 and
and 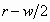 since the area is since the area is 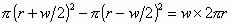 as expected.
as expected.
It is the most reasonable extension to define the corresponding width
in 3D as the circle in the perpendicular plane with its centre at the point
on the curve. The definition is acceptable at least for the torus 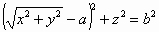 that is formed by rotating the smaller circle of radius
that is formed by rotating the smaller circle of radius 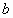 with bigger radius
with bigger radius 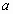 , whose
volume is given by , whose
volume is given by 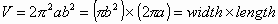 .
The easiest and the most elegant way to understand the relation is that
the sections for any constant value of .
The easiest and the most elegant way to understand the relation is that
the sections for any constant value of 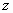 where
where 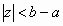 is a pair of concentric
circles by reducing to 2D case. is a pair of concentric
circles by reducing to 2D case.
3 THE SIMPLEST SPATIAL CURVE: CIRCULAR HELIXES
A straight line is the most homogeneous line with a constant direction
but without any curvature and can be in one dimension. A circle is the
most homogeneous line with a constant curvature but without any twist (rotation
+ translation) and is two-dimensional. A circular helix is the simplest
essentially three-dimensional curve, being the most homogeneous line with
a constant twist, never realize in lower dimensions than three. The curve
in Cartesian coordinate is given by 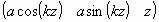 and in cylindrical coordinate
and in cylindrical coordinate 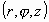 by and
by and 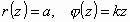 where where 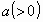 stands for the radius of the cylinder on the surface of which the circular
helix lies and constant
stands for the radius of the cylinder on the surface of which the circular
helix lies and constant 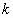 depends on the pitch. Regard
depends on the pitch. Regard 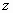 as time, then it is nothing but pure rotation in a plane. The torsion of
the curve (Coxeter, 1961, 1969, pp. 323-325, where
as time, then it is nothing but pure rotation in a plane. The torsion of
the curve (Coxeter, 1961, 1969, pp. 323-325, where 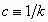 is used) is given by
is used) is given by 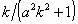 .
A helical surface can be regarded as a set of the circular helix with common
value of .
A helical surface can be regarded as a set of the circular helix with common
value of 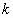 and for arbitrary
value of and for arbitrary
value of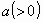 . It is defined as
the locus of rotating horizontal straight line around a fixed vertical
line. A circular helix is the section of a helical surface and a cylinder
of radius . It is defined as
the locus of rotating horizontal straight line around a fixed vertical
line. A circular helix is the section of a helical surface and a cylinder
of radius 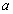 . It is natural
to introduce the concept of helical symmetry for the circular helixes
belonging to a common helical surface. Reminisce that a step stone of helical
staircase is triangular (neglecting the limiting part close to the central
axis). The slope of the staircase depends on the distance from the axis;
infinite at the axis and tends to zero in infinite remote. . It is natural
to introduce the concept of helical symmetry for the circular helixes
belonging to a common helical surface. Reminisce that a step stone of helical
staircase is triangular (neglecting the limiting part close to the central
axis). The slope of the staircase depends on the distance from the axis;
infinite at the axis and tends to zero in infinite remote.
Let us focus on the problem of giving a single circular helix a thickness.
Now, 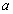 is a constant and
an angle is a constant and
an angle 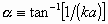 is introduced.
Prepare a sheet of paper on which parallel lines of slope angle is introduced.
Prepare a sheet of paper on which parallel lines of slope angle 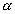 are drawn with the periodic separation of
are drawn with the periodic separation of 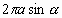 (the corresponding period in intercept is
(the corresponding period in intercept is 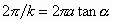 )
as shown in Fig.1. Then, put it on the surface of cylinder so that the
horizontal axis just fits around the cylinder of radius )
as shown in Fig.1. Then, put it on the surface of cylinder so that the
horizontal axis just fits around the cylinder of radius 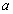 and then the parallel lines make a single slope. For
and then the parallel lines make a single slope. For 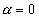 and then
and then 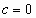 , a circle is
obtained. For , a circle is
obtained. For 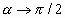 then then 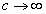 ,
the helix tend to a straight line corresponding to the generating line
of the cylinder. ,
the helix tend to a straight line corresponding to the generating line
of the cylinder.
3.1 The densest helixes with thickness
Though the value of 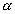 is arbitrary as a line, there exists the minimum value if the finite thickness
is given to the helix and then the volume exclusion effect is introduced.
Obtaining the minimum value of slope angle is rather complicated. All the
circular sections are inclined and there are no diameters parallel to the
axis line. It means that the ends of diameters tend to go remote but radial
ones. This effect in 3D space causes some confusion. Can you imagine the
inner structures and the several planer sections, for example, horizontal
and vertical? Another case that can be treated in parallel is double helix.
In the cases of more than two helical lines, there are vacant space around
the central axis, as easily seen from the fact that there are no point
in a plane that three impenetrable circles can share. Therefore it is necessary
to start the analysis with how three cylinders symmetrically contact one
another.
is arbitrary as a line, there exists the minimum value if the finite thickness
is given to the helix and then the volume exclusion effect is introduced.
Obtaining the minimum value of slope angle is rather complicated. All the
circular sections are inclined and there are no diameters parallel to the
axis line. It means that the ends of diameters tend to go remote but radial
ones. This effect in 3D space causes some confusion. Can you imagine the
inner structures and the several planer sections, for example, horizontal
and vertical? Another case that can be treated in parallel is double helix.
In the cases of more than two helical lines, there are vacant space around
the central axis, as easily seen from the fact that there are no point
in a plane that three impenetrable circles can share. Therefore it is necessary
to start the analysis with how three cylinders symmetrically contact one
another.
3.2 How are the fine structures inside?
It is interesting to imagine the hidden fine structures inside. For
example, how a circular section contact with another circular sections
and how they arrange? Interesting problems arise step by step. From an
educational point of view, it is desirable to have, to imagine the situation,
and to enjoy such kind of questions even if they cannot find the answer.
It will motivate towards many directions such as mathematics, science,
designing etc.
The procedure for the author to answer those problems is based on the
fact that a helices with thickness is set of helixes with common value
of 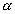 . All of the helical
lines with . All of the helical
lines with 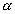 that passes
in inside of a circle go keeping the whole shape. Then one can trace all
of the positions on the trajectories or flow line. See the figures here
showing the situation. Some of the figures here are exhibited with some
explaining text at gallery. More figures containing some sections will
be added in the oral presentation. that passes
in inside of a circle go keeping the whole shape. Then one can trace all
of the positions on the trajectories or flow line. See the figures here
showing the situation. Some of the figures here are exhibited with some
explaining text at gallery. More figures containing some sections will
be added in the oral presentation.
| a) |
b) |
c) |
d) |
e) |
f) |

|
|
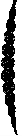
|
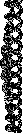
|

|

|
|
Figure 1. The
densest single helix (left to right) a) from a side, b) from upper,
c) a part of touching discs, d) the same disks with the core helix, e)
the same as just before from upper, f) the same from a slightly sifted direction.
|
| a) |
b) |
c) |
d) |
e) |
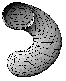
|

|

|
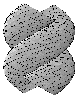
|

|
|
Figure 2: The densest double
helix (left to right) a) one of two elements,
b) the other element, c) combining them, d) view of the combined one
from a symmetrical direction, e) the same from the opposite side.
|
References
Coxeter, H. S. M. (1961)
Introduction
to Geometry, New York: Wiley; 2nd ed., ibid., 1969.
Ogawa, T. (2004) Geometry of the beauty III: Space curves
with constant section, Bulletin of the Society for Science on Form,
Vol.19, No.1, p. 32-33 [in Japanese].
Ogawa, T. (2004) Geometry of the Beauty IV: Densest-single
helix and double-helix with constant section and some other topics,
to be published in Bulletin of the Society for Science on Form Vol.19,
No.2 [in Japanese].

|