|
FROM MATHEMATICS TO ART: AN EXAMPLE
FRANCISCO RUIZ AND NURIA JUNCOSA
1 INTRODUCTION Sometimes, people with common interests take diverging ways, but occasionally one dares to explore another fields of knowledge to look for another ways to make inquiries in his own field. Very often mathematics and graphic works have been considered as not related subjects, with not too many connections between them. This paper consists of two diverse parts. In the first one we make a summary of the work of the professor of Mathematics who has used algebraic structures, such as group structure, for the teaching of Mathematics, in a university context of teacher training (Ruiz and Peñas, 2002). In order to visualize the additive and multiplicative groups of the residual classes Zn students substitute the numeric symbols for certain colored visual patterns in the corresponding Pythagorean table, in order to highlight the regularities in the groups. Visual Mathematics has become an important reference point
in researching in Mathematical Education. Sensory perception is an important
way to access knowledge. It is appropriate to consider the intervention
of the senses in the transmission, acquisition and construction of any
type of mathematical knowledge. Visual information as a generator of images
and mental objects provides an important function in learning mathematics.
The capability to visualize any mathematical concept or problem requires
experimentation to interpret and understand figurative information about
the concept and be able to manipulate it mentally, as well as to express
it visually. The study of algebraic structures usually presents difficulties
because of its degree of abstraction. The visualization of elements of
these structures can facilitate their recognition and the understanding
of some properties.
2 THE AIMS OF THE EXPERIENCE The main goals in this work are: - Using representations in order to bring the existing connections between Algebra and Geometry to students.As the connections between the fields of knowledge that compose mathematics are not evident for our students, we should promote experiences that relate them, and let future teachers make connections between Algebra and Geometry, by creating geometric patterns that highlight algebraic properties and relationships. - Using motivational elements for the students like the use of resources such as materials and computers, because the use of physical and technological methods can help to increase the pleasure of learning mathematics for students who have difficulties with abstract concepts. - Strengthening the creativity of students by means of
drawing artistic designs, since it has a decisive influence on the acquisition
of certain learning skills that ought to be acquired gradually. This creativity,
in our experience, is linked to the perception of shapes and patterns,
and it facilitates establishing a connection between numbers and geometric
figures.
3 THE STUDY The intention of our study was to answer questions such as the following: · What do we achieve by replacing numeric symbols with geometrical ones? · Is visualization of the properties of algebraic structures facilitated in this way? · Can we perform geometric transformations upon these tables? · What is the role of computers in these activities? The experience involved two groups of primary student teachers at the University of Granada in two different sessions. The first one took place during the 1992/93 academic year. The lecturer made a short presentation with transparencies in black and white, and the work was done by hand, using a photocopier and several kinds of paper or transparencies. The second experience took place during the year 2001/02. The same short presentation was made by the lecturer but on this occasion he used a computer, with the same figures using color. Our purpose was that the students:
In order to represent numbers, mathematicians use symbols,
which are special drawings with very well known meanings. What would happen
if we substitute numerical symbols by geometrical drawings?
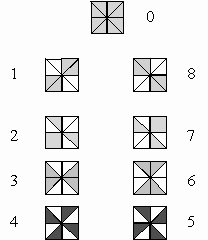
Figures 1 and 2 display the example shown to students in order to present the tasks. In the table corresponding to (Z9,+),
there are numeric regularities. After substituting each numeric symbol
with its corresponding geometric figure, we obtain an isomorfic table (fig.
2) that can be modified by geometric transformations such as reflections
or rotations (Forseth, S. and Troutman, A., 1974). (figure 3).
Now, the students must go into in the algebraic structures
working on their own, to find properties and regularities, identify structures
visually and carry out artistic designs using different variables, like
additive or multiplicative structure, module, shapes of each element, color,
shapes of the table (different grids), geometric transformations and deformations
using computers programs.
|