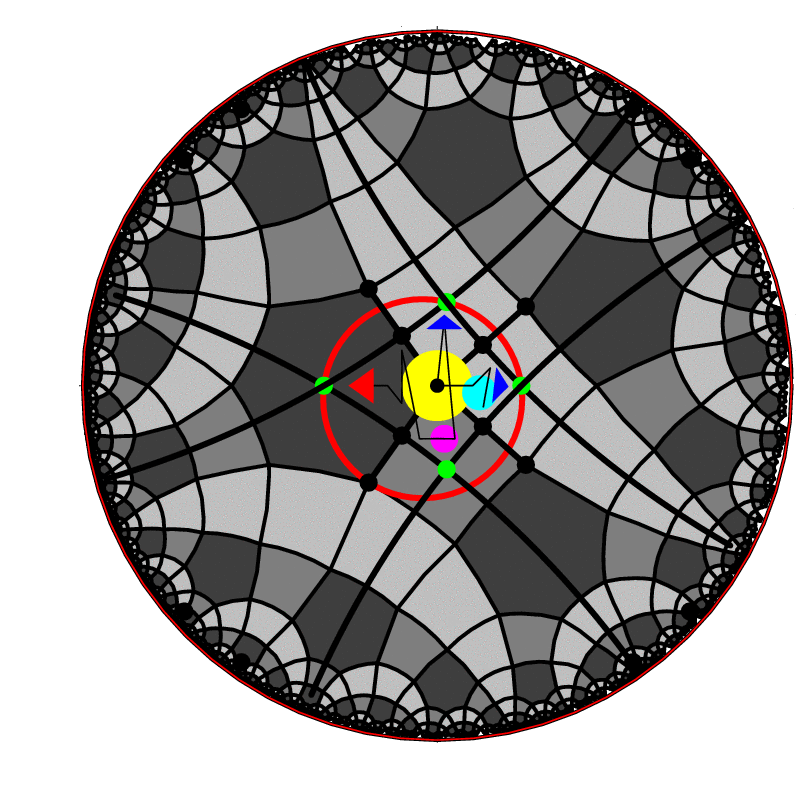
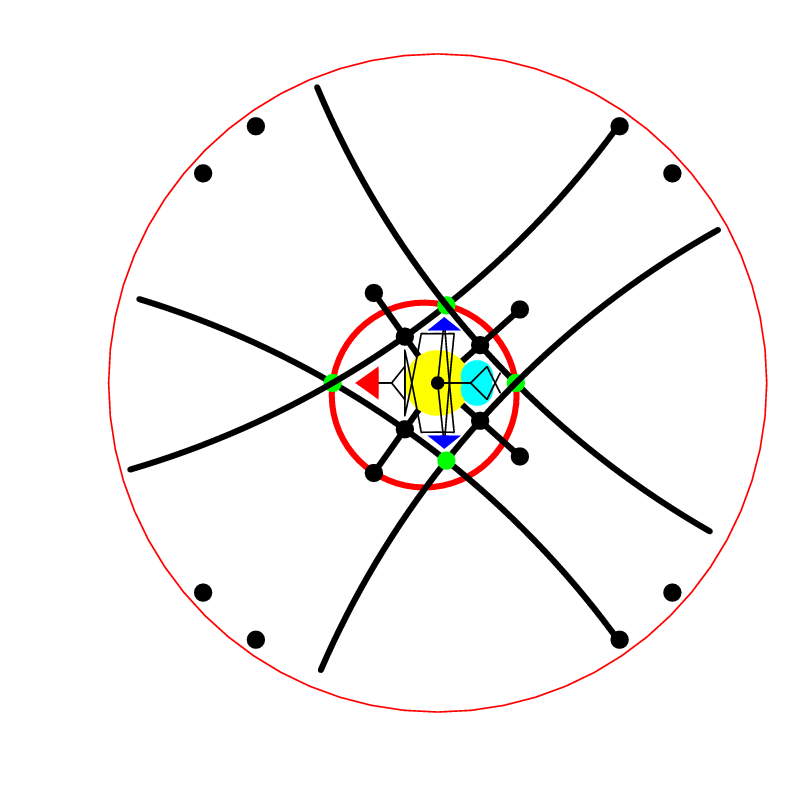
Images obtained by tessellating hyperbolic plane usually show simple symmetric patterns and now we will focus on creating more intricate ones. As a base we use tessellation given with its vertex type (n₁, n₂,…,n_N) meaning that the polygons about this vertex in cyclic order are an n₁-gon, an n₂-gon, . . . and an n_N-gon, where N is the number of polygons at each vertex. By connecting the incenters of adjacent polygons/tiles surrounding a vertex, an N-gon is formed. Basic domain is this N-gon or   one of the polygons of its decomposition into congruent polygons based on its internal symmetries. In the most cases it is the actual fundamental domain (or several adjacent fundamental domains connected), but it is always sufficient to construct the whole tessellation. The transformation rules of the tessellation combined with an arbitrarily chosen motif contained in the fundamental domain (Fig. 3c) enables us to create infinite number of variations of every hyperbolic tessellation.

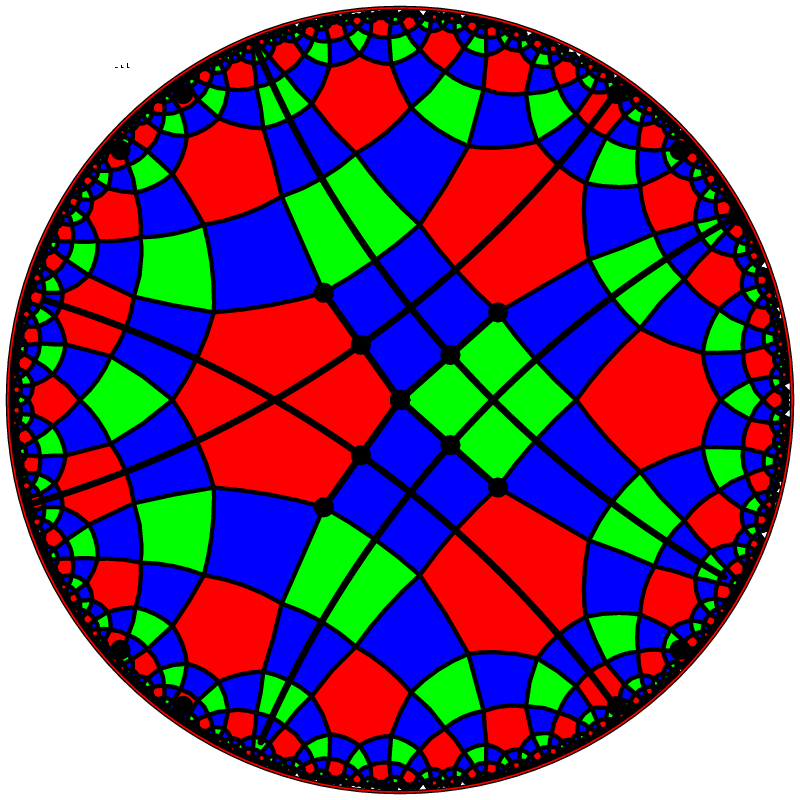
Figure 3. (a) Uniform tessellation (4,4,4,6);

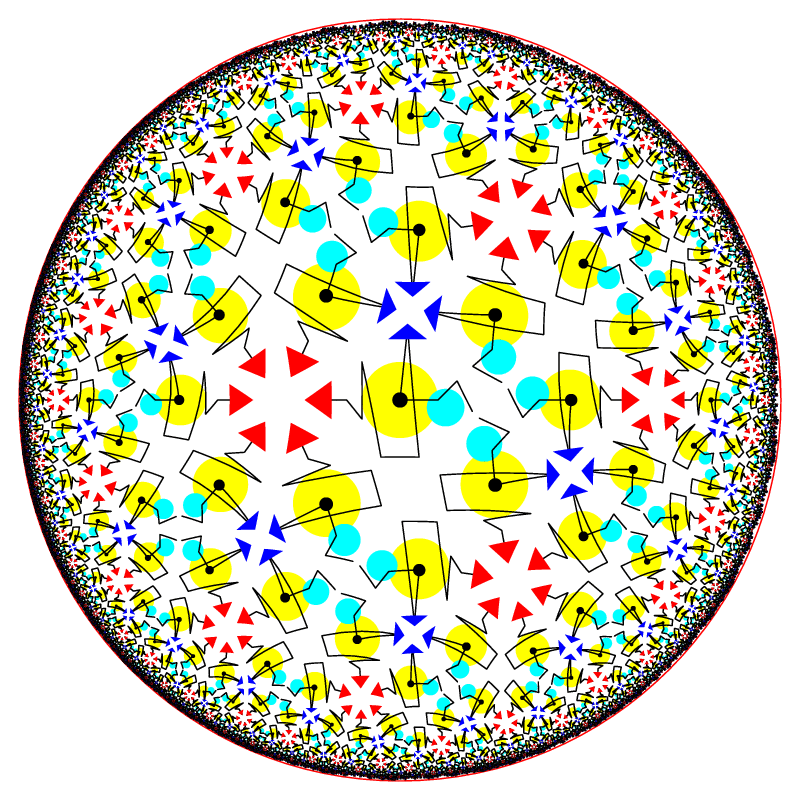
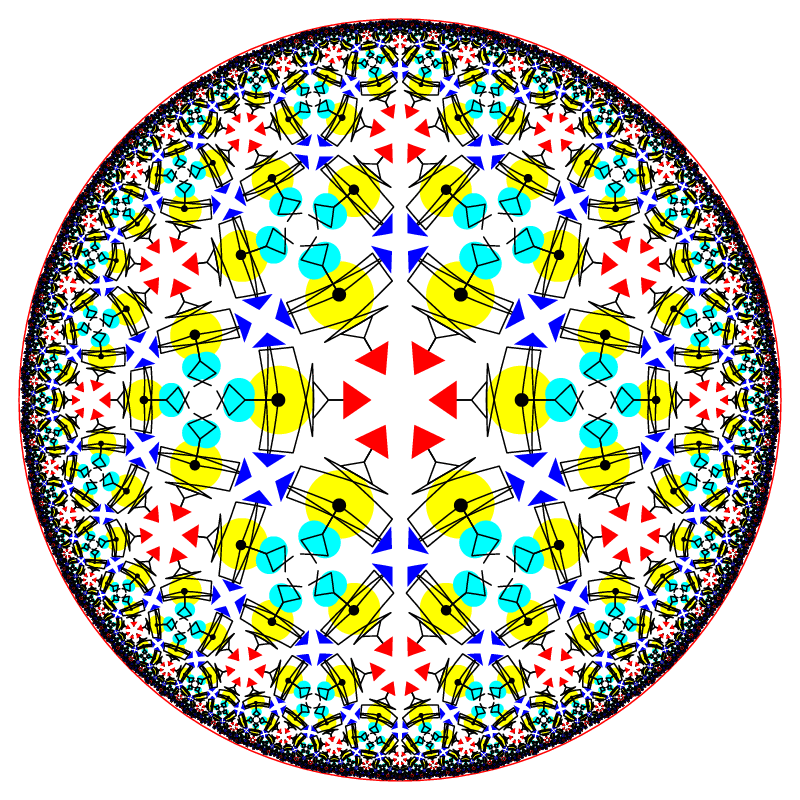
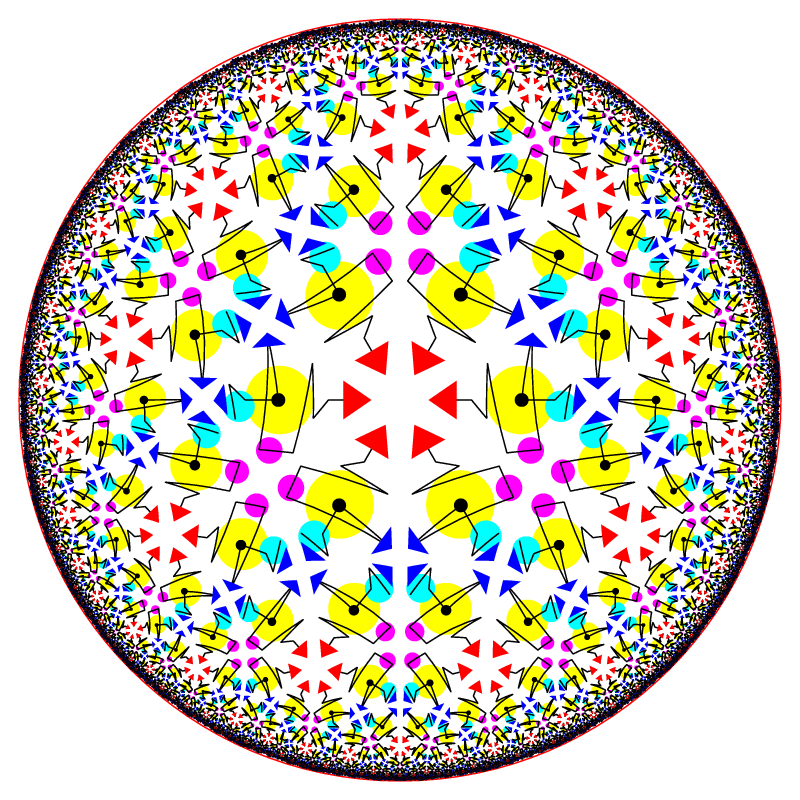
Based on a choice of the motif, a single tessellation can appear totally different (Fig. 4): manifest symmetries that were not present, stay the same if the motif exhibits local symmetries consistent with the symmetries of the entire tessellation while asymmetric motif can hide symmetries that tessellation admits.

The same method can be applied to hyperbolic tessellations presented in Poincare half-plane and Klein disk models, or to Euclidean or spherical tessellations. However, this is still relatively unexplored area with many open questions: finding all different possible shapes of the fundamental region, analysing knot patterns and aperiodic tessellations, etc. Once the whole method is implemented, there will be more room for personal artistic expression, in order to emphasize intrinsic beauty of hyperbolic geometry and its interrelations with art and design.