|
ANALYSIS OF TWO HOUSINGS IN SYMMETRY
JIN-HO PARK
1 INTRODUCTION Symmetrical operations often prevail in housing designs as underlying
principles of their spatial composition. Their applications in housing
designs are manifold. They apply to the overall housing organization as
a whole. They also apply to a standard unit with its typological variations
and the grouping of multiple units into a larger assemblage. When a standard
unit and its variations are arranged in a mixture at a larger site, possibilities
of their groupings will be considerably increased. A single housing unit
may be symmetrical or asymmetrical. If a housing unit has a high level
of individual symmetry, the number of ways in which it may be multiplied
and grouped is usually limited. Nevertheless, if a unit is asymmetrical,
the number of combinations is potentially increased and maximized. In architecture,
bilateral symmetry is the most often encountered concept of symmetry in
the classical period. In the twentieth century, architectural designers
have explored various symmetries other than traditional bilateralism. They
exploit all four types of the planar symmetry transformations–reflection,
translation, rotation, and glide reflection–to building designs.
2 A NOTE ON SYMMETRY METHODOLOGY Symmetries are defined as spatial transformations that maintain the congruent configuration of an object without changing its appearance as a whole. In two dimensions, there are two symmetry groups of plane symmetry: finite group and infinite group. The finite group of plane symmetry is called the point group. Spatial transformations take place in a fixed point or line. The transformations involve rotation about the point and reflection along the lines, or the combination of both. In the point symmetry group, no translation takes place. In the infinite symmetry group, spatial transformations occur where the basic movement is either translation or a glide reflection. In this group, designs, which are invariant under one directional translation, are called the frieze group, and designs under two directional translations are called the wallpaper group (March and Steadman, 1971). In our discussion, emphasis is given to the application of point group
symmetry of the regular polygon, in particular, the square, since the symmetry
of the square prevails in architectural design (Weyl, 1952). There are
two finite point groups in the plane: Cn (cyclic group)
and Dn (dihedral group) where n represents the
period of the group or the number of 360/n rotations. The number
of elements in a finite group is called its order. The symmetry group of
Dn
has order 2n elements, while Cn has order n
elements (Park, 2000). The symmetry group of the square is the dihedral
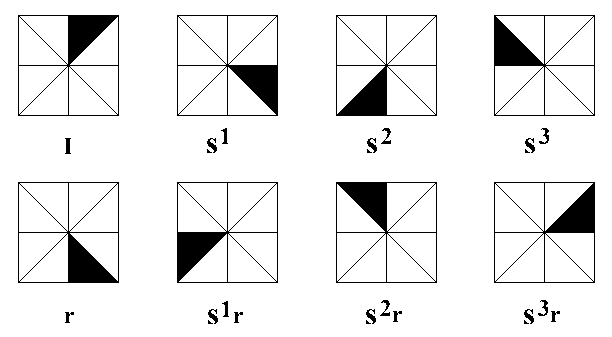
group D4 of order 8. There are eight distinguishable
transformations, which comprise this group (Fig. 1).
Figure 1: The symmetry
operations of a square labelled as I, s1, s2,
s3,
r,
s1r, s2r,
s3r.
We obtain all the eight symmetry operations by combining two basic operations,
quarter turn and mirror reflection. The properties construct the multiplication
table of the symmetry group of the square where all possible eight transformations
can be computed. Cayley diagram is another way of computing those elements
where a sequence of multiplications can be tracked down. With this diagram,
the symmetry group of the square can be computed to produce all of the
other elements, one out of eight transformations in the case of the symmetry
of the square. Equipped with the mathematical tools in mind, we analyze
housing designs with regard to their use of symmetry.
3 F.L. WRIGHT’S QUADRUPLE BUILDING BLOCK Frank Lloyd Wright’s social housing project, called the Quadruple Building
Block, is analyzed with regard to its use of symmetry. Wright uses a standard
unit plan for the project. Whereas the unit itself is asymmetric, a various
local symmetries are involved in the unit. The assembly in their site layout
includes two ways: One is the pinwheel type (C4), and
the other is the mirrored reflection type (D2). Each
house is set on four equally subdivided lots, sharing a common backyard
in the center for all four houses. The first scheme shows a pinwheel clustering
of four individual houses around the corner of a square site. Each house
orients a different direction but has its own entry that faces the street.
The second scheme shows each of the clustering of four houses lining both
sides of the street in a mirrored format (D2) based on
the tartan grid (McCarter, 1997). The whole complex of the housings is
laid out in a way that their elevation can be varied according to their
arrangement. The symmetric transformation denotes differences in exterior,
providing variety in the streetscape. His consecutive housing designs have
been developed throughout his career, yet they share a common compositional
theme: the pinwheel type of symmetry. It has been a recurring theme in
his housing designs. Such a recursive theme is considered as the source
of continuity of theme and variations in housing designs.
4 R. M. SCHINDLER’S THE SCHINDLER SHELTER R. M. Schindler, who used work for Wright, follows Wright’s footstep
in the use of symmetry. His symmetry application in housing design is highlighted
in his unexecuted Schindler Shelter project, developed from 1933 to 1942.
We observe that the overall floor plan is based on 5-foot square grid (with
the Schell construction). Along with the square grid, the symmetry governs
the internal structure of the spatial composition in each shelter unit
as well as the unit variations. The internal organization is subdivided
by the removable closet partitions for spatial flexibility and set along
the pinwheel type of rotational symmetry (Park, 2001). Then, the garage
is added to any side of the house as a separate unit. Instead of providing
only a standard unit with fixed layouts, a series of variations are provided.
They share the same underlying organizational system.
5 SUMMARY Symmetry as an underlying principle of housing designs has been discussed
for the analysis and synthesis of housing designs. Some techniques such
as multiplication table and Cayley diagram has been introduced as analytic
methods. Wright and Schindler’s housing designs have been comparatively
analyzed. Their use of the symmetry method in the housing designs is strikingly
similar. Skylight designs are analyzed to enhance their conscious applications
of the methods not only in major building designs but also in minor details.
References McCarter, R. (1997) Frank Lloyd Wright, London: Phaidon Press Limited Park, J.-H. (2000) Subsymmetry analysis of architectural designs: Some example, Environment and Planning B: Planning and Design,27, 121-136. Park, J.-H. (2001) Analysis and synthesis in architectural designs: A study in symmetry, Nexus Network Journal, 3, No. 1, http://www.nexjournal.com/Park.html Weyl, H. (1952) Symmetry, Princeton: Princeton University Press.
|