|
ON SOME REGULAR TOROIDS
LAJOS SZILASSI
|
Name: Lajos Szilassi (b. Szentes,
Hungary, 1942).
Address:Department
of Mathematics, Juhász Gyula Teachers Training College, University
of Szeged,
Boldogasszony str 6, Szeged, H-6701 Hungary; E-mail: szilassi@jgytf.u-szeged.hu
Fields of interest:Geometry (polyhedra),
Computer graphics, (programming, visualization).
Publications: Szilassi, L.
(1986) Regular toroids, Structural Topology, [Montreal], No. 13,
pp. 69-80.
|
| Abstract: As it is known, in a regular polyhedron
every face has the same number of edges and every vertex has the same number
of edges, as well. A polyhedron is called topologically regular if further
conditions (e.g. on the angle of the faces or the edges) are not imposed.
An ordinary polyhedron is called a toroid if it is topologically torus-like
(i.e. it can be converted to a torus by continuous deformation), and its
faces are simple polygons. A toroid is said to be regular if it is topologically
regular. It is easy to see, that the regular toroids can be classified
into three classes, according to the number of edges of a vertex and of
a face. There are infinitely many regular toroids in each class, because
the number of the faces and vertices can be arbitrarily large. Hence, we
study mainly those regular toroids, whose number of faces or vertices is
minimal, or that ones, which have any other special properties. Among these
polyhedra, we take special attention to the so called „Császár-polyhedron",
which has no diagonal, i.e. each pair of vertices are neighbouring, and
its dual polyhedron (in topological sense) the so called „Szilassi-polyhedron",
whose each pair of faces are neighbouring. The first one was found by Ákos
Császár in 1949, and the latter one was found by theauthor,
in 1977. |
1 ON THREE CLASSES OF TOROIDS
For simple (sphere-like) polyhedra, Euler's formula V - E + F = 2
holds,
where V, E and F are the numbers of vertices, edges and faces, respectively.
For toroids Euler's formula is modified to V - E + F = 0. Studying
toroids, we cannot expect all of the faces or solid angles to be regular
and congruent, so the description regular here is clearly a topological
property.
Assume each face of a regular toroid has a edges, and at each
vertex exactly b edges meet. We can distinguish three classes of
regular toroids, according to the numbers of edges incident with each face
and each vertex:
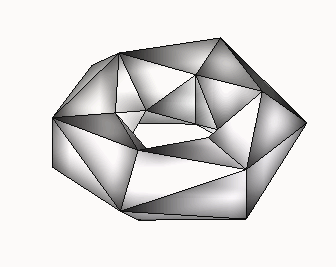 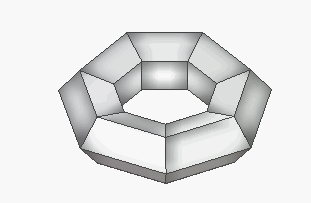 
Figure 1:
class T1 : a=3, b=6; class T2:
a=4, b=4; class T3,: a=6, b=3;
However, it is interesting to determine for each class the lowest number
of faces or vertices required to construct a regular toroid in that class,
possibly with the restricting condition that the faces or solid angles
belong to as few congruence classes as possible.
2 THE CSÁSZÁR –POLYHEDRON
At every vertex of a regular toroid in class T1 exactly
six edges meet, so that such a toroid has at least seven vertices.
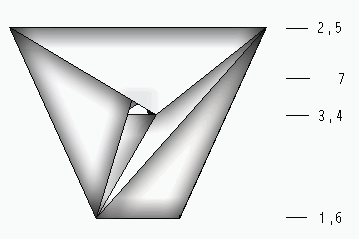
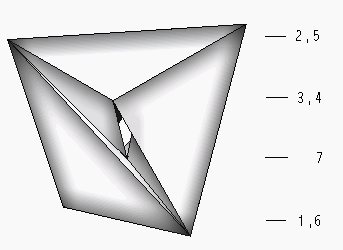
The Császár polyhedron [1], [3], [9] (pp. 244-246) is
such a toroid with only seven vertices. This polyhedron does indeed belong
to class T1 for any two of its vertices are joined by
an edge, and thus six edges meet at each vertex. The number of its vertices
is the lowest possible not only in class T1 , it can
readily be seen that a toroid with less than seven vertices does not exist.
The toroid, which is constructed on the basis of the data published by
Professor Ákos Császár at Budapest University who
is a member of the Hungarian Academy of Sciences [3], appears "fairly crowded".
We have prepared a computer program to search for a "less crowded" version.
Without going into the details a formal definition (which would need
oriented matroid terms [2]), we only restrict ourselves to an intuitive
description as follows. Let us consider two models of Császár
polyhedron essentially congruent if:
-
one of the polyhedra can be transferred into the other by gradually changing
the coordinates of one of the polyhedra without causing self intersection
in the surface;
-
one of the polyhedra can be transferred into the other by reflection;
-
one of the polyhedra can be transferred into the other by executing the
above operations one after another;
otherwise the two Császár-polyhedra are essentially different.
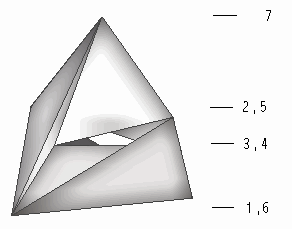
J. Bokowski and A. Eggert proved in 1986 that the Császár
polyhedron has only four essentially different versions.[1]
It is to be noted that in topological terms the various versions of
Császár polyhedron are isomorphic, there is only one way
to draw the full graph with seven vertices on the torus.
|
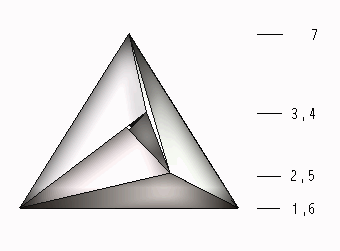
|
 |
 |
 |
|
Figure 2. The full graph with seven vertices that can be drawn
on the torus |
3 POLYHEDRA FROM CLASS T2
Class T2 of regular toroids consists of those torus-like
ordinary polyhedra in which four edges meet at each vertex and the faces
are quadrilaterals. (Figure 3.) This type of regular toroids is
the easiest to construct.
|

|
 |
 |
|
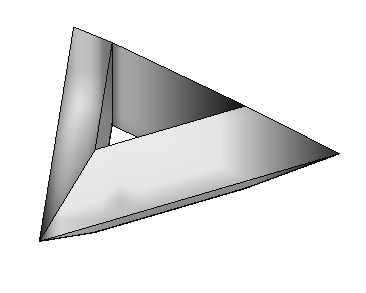
Figure 3. Two toroids with 35 faces, and one with min (9) faces
in class T2 |
It is not known whether there exists a regular toroid in T2
with 10 or 11 faces (vertices), though a graph having 10
or 11 vertices (and regions), and which belongs to T2,
class can be drawn on torus.
4 SOME POLYHEDRA FROM CLASS T3
When constructing toroids belonging to class T3,
care
should be taken to make sure that the six points defining one region (face)
are in the same plane. This requirement can be easily met, if the toroid
has "sufficiently high number" of faces. (Figure 1.) We have just
created some interesting regular toroid consisting of 24, 9 and of 7 faces
only (Figure 4).
As we have seen, the most important property of the Császár
polyhedron is that any two vertices are joined by an edge. There is a very
close relationship, so-called duality, between this polyhedron and the
polyhedron with the lowest number of faces in class T3,
the main characteristic of the latter being that any two faces have a common
edge This relationship is partly topological, however, if we create a new
polyhedron by using projective transformation from a given polyhedron,
(e.g. polarity with respect to a sphere), then the new polyhedron may be
a self-intersecting one.
|

|
 |
 |
|
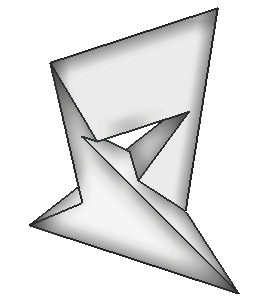
Figure 4. Toroids from class T3 with 24, 9 and 7 faces |
The author of this paper constructed this seven-faced polyhedron in
1977 after producing the dual of the Császár polyhedron by
using polarity. The new polyhedron obtained by this way, had self-intersecting
faces, too. A computer assisted analysis had used to find the undesired
intersections, and by modifying the data could be obtained the above polyhedron
bordered by simple polygons. (Figure 4.) If a model of the structure is
known, it is easy to develop a simple method to construct the polyhedron.
This polyhedron is topologically isomorphic with Heawood's toroidal map
with seven colours. (It was Martin Gardner who used the term "Szilassi
polyhedron" for the first time to identify this polyhedron [4].) In 2004
J. Bokowski and L. Schewe has proved that the Szilassi polyhedron had essentially
only one axially symmetric version [2].
References
[1] Bokowski, J. and Eggert, A.
(1991) All realizations of Möbius' torus with 7 vertices,
Structural Topology, No. 17, pp. 59-78.
[2] Bokowski, J. and Scewe, L. (2004) On Szilassi’s
Torus, Preprint Technishe Hochschule Darmstadt.
[3] Császár, Á. (1949) A polyhedron
without diagonals, Acta Sci. Math. Universitatis Szegediensis, 13,
140-142.
[4] Gardner, M. (1978) The minimal art , Scientific
American, 1978/11.
[5] Gardner, M. (1992) Fractal Music, Hypercards, and
More Mathematical Recreations from Scientific American Magazine,
New York: W. H. Freeman, 118-120.
[6] Gruber, P.M. and Wills, J.M. (1993) Handbook of
Convex Geometry, Amsterdam: North-Holland.
[7] Grünbaum, F. (1994) Polytopes, Kluwer
Academic Publishers.
[8] Kappraff, J. (2001) Connections: The Geometric
Bridge between Art and Science, Singapore: World Scientific.
[9] Szilassi, L. (1986) Regular toroids, Structural
Topology, No. 13, 69-80.
[10] Stewart, B. M. (1980) Adventures Among the Toroids,
Revised 2nd edition, Okemos, Michigan.

|