ON RANDOM PACKING OF SPHERES:
RETROSPECTIVE OVERVIEW
MASAHARU TANEMURA
Name: Tanemura, M. (b. Shiga,
Japan, 1946).
Address:The
Institute of Statistical Mathematics, 4-6-7 Minami-Azabu, Minato-ku, Tokyo
106-8569, Japan.
E-mail: tanemura@ism.ac.jp
Fields
of interest: Stochastic geometry, spatial statistics,
mathematical crystallography
| Abstract: We first extend
the Rényiís car parking problem to the random sequential packing
problem of spheres in D-dimensional space. Then, the difficulty of analytic
treatment of the problem for higher dimensions more than one is pointed
out. It is shown that this compels us to the investigation by computer
simulations. In order to get a complete packing, an efficient algorithm
with the help of Voronoi tessellation is presented. Then, current values
of packing densities for 2D and 3D random sequential packings are given.
Possibility of deriving packing densities for higher dimensional spaces
is also suggested. |
1 RANDOM CAR PARKING PROBLEM AND ITS EXTENSION
In 1958, a Hungarian mathematician, Alfréd Rényi, presented
an interesting problem: "We place at random on the interval (0, 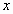 )
unit intervals not having points in common. What is the expected number )
unit intervals not having points in common. What is the expected number 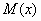 of
intervals we can thus place on (0, of
intervals we can thus place on (0, 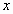 )?".
By assuming the unit interval a car on the road, the problem is often called
"random car parking problem". Rényi (1958) solved this problem analytically
and has obtained the solution )?".
By assuming the unit interval a car on the road, the problem is often called
"random car parking problem". Rényi (1958) solved this problem analytically
and has obtained the solution 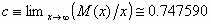 . .
As a simple extension of the random car parking problem, Rényi
(1958) proposed a homothetic parking of unit cubes. Palásti (1960)
conjectured from her computer simulations that the mean packing density 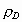 for D-dimensional space should have the following simple form
for D-dimensional space should have the following simple form 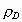 = = 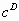 ,where ,where 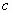 is
the solution defined above. is
the solution defined above.
This relation 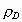 = = 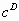 is
quite appealing if it is true. Some people therefore have concentrated
their attentions on ascertaining Palastiís conjecture. Present status of
this conjecture is presented in Solomon and Weiner (1986) and the deviations
between experimental findings and Palástiís conjecture are clearly
shown there. These facts indicate that it is very difficult to treat the
problem analytically for is
quite appealing if it is true. Some people therefore have concentrated
their attentions on ascertaining Palastiís conjecture. Present status of
this conjecture is presented in Solomon and Weiner (1986) and the deviations
between experimental findings and Palástiís conjecture are clearly
shown there. These facts indicate that it is very difficult to treat the
problem analytically for 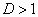 and
that we are compelled to perform computer simulations. and
that we are compelled to perform computer simulations.
Random sequential packing by spheres in 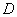 -dimensional
space can be thought of as another simple extension of the "random car
parking problem". The procedure of random sequential packing of congruent -dimensional
space can be thought of as another simple extension of the "random car
parking problem". The procedure of random sequential packing of congruent 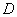 -dimensional
spheres is quite simple: The centre of the first sphere is uniformly sampled
in the container and it is put there; and, in general, after -dimensional
spheres is quite simple: The centre of the first sphere is uniformly sampled
in the container and it is put there; and, in general, after 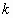 spheres
have been placed, the spheres
have been placed, the 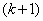 -st
sphere is placed in such a way that its centre is uniformly distributed
in the region which is occupiable for the centre, that is, in the set of
points where the sphere does not overlap with any of the previously placed
spheres. The process ends when there is no region available for a further
sphere, and we call this final state a "random complete packing" (Tanemura,
1979). This kind of packing of spheres has many practical applications
(see, for instance, Evans, 1993). -st
sphere is placed in such a way that its centre is uniformly distributed
in the region which is occupiable for the centre, that is, in the set of
points where the sphere does not overlap with any of the previously placed
spheres. The process ends when there is no region available for a further
sphere, and we call this final state a "random complete packing" (Tanemura,
1979). This kind of packing of spheres has many practical applications
(see, for instance, Evans, 1993).
2 ALGORITHM FOR COMPLETE PACKING THROUGH VORONOI TESSELLATION
The most simple-minded algorithm which corresponds to the packing procedure
stated above might be the following: the coordinates of the centre of a
"test" sphere are determined by a random point which is uniformly distributed
within the container. If the test sphere does not overlap with spheres
already put, it is then put at that position. Otherwise, the test sphere
is discarded and another test sphere is generated. The process is repeated
until a certain stopping rule is fulfilled (hereafter, the total number
of test spheres, 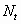 , is
used as a stopping condition: when the total number of test spheres exceeds , is
used as a stopping condition: when the total number of test spheres exceeds 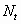 ,
the procedure ends). ,
the procedure ends).
We call the above procedure of packing a "simple rejection scheme".
It is seen that, by using only the simple rejection scheme, it is almost
hard to attain a complete packing when the size of the container is adequately
large compared with the size of each sphere. Figure 1 illustrates this
circumstance (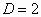 ). Let the container
be a square box ). Let the container
be a square box 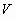 whose
size is whose
size is 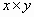 where the unit
of length is the diameter where the unit
of length is the diameter 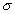 of
packed disc of
packed disc 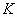 . In Fig.1, . In Fig.1, 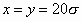 is
used. White 264 discs are put by using is
used. White 264 discs are put by using 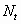 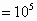 test
discs, while dark seven discs and white ones are obtained for test
discs, while dark seven discs and white ones are obtained for 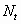 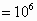 test
discs. Black three discs in Fig.1 are not placed by test
discs. Black three discs in Fig.1 are not placed by 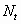 test
discs smaller than test
discs smaller than 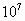 and
they are actually obtained by the complete packing algorithm we present
below. Note that the torus (periodic boundary condition) is used in this
packing. Thus we take two stage strategy: (1) the stage of simple rejection
scheme; and (2) the stage of complete packing. and
they are actually obtained by the complete packing algorithm we present
below. Note that the torus (periodic boundary condition) is used in this
packing. Thus we take two stage strategy: (1) the stage of simple rejection
scheme; and (2) the stage of complete packing.
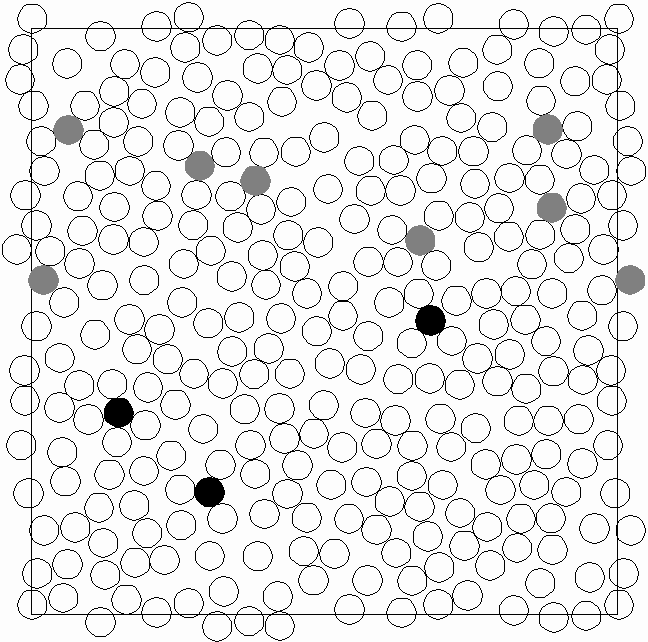
Figure 1: Illustration of 2D random sequential packing.
Black discs are placed by applying CPA.
2.1 Complete packing algorithm (CPA)
Let us assume, after the first stage of simple rejection scheme by using 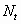 test
spheres, k spheres test
spheres, k spheres 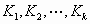 are
placed in the container are
placed in the container 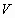 .
To each of .
To each of 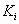 , let us assign
a large sphere , let us assign
a large sphere 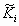 whose radius
is twice that of and concentric with whose radius
is twice that of and concentric with 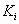 .
For this set of spheres, we perform the Voronoi tessellation. Then, the
essential part of the complete packing algorithm (abbreviated by "CPA")
is the followings: .
For this set of spheres, we perform the Voronoi tessellation. Then, the
essential part of the complete packing algorithm (abbreviated by "CPA")
is the followings:
Step B1. Detection of the position of occupiable space. By
inspecting all of the Voronoi vertices, we can list up vertices which is
not covered by any of 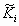 .
We call each vertex listed here an open vertex. If there is no open vertices,
then CPA ends. .
We call each vertex listed here an open vertex. If there is no open vertices,
then CPA ends.
Step B2. Division and classification of occupiable regions. Here,
all of the Voronoi edges are inspected by using open vertices.
Step B3. Placement of a new sphere into the occupiable region.
Step B4. Performing Voronoi tessellation for the new configuration
of spheres. Go to Step B1.
3 CURRENT RESULTS FOR 2D, 3D RANDOM PACKING DENSITIES
AND THE POSSIBILITY OF EXTENSION TO HIGHER DIMENSIONS
Tanemura (1981, 1988a, b) had presented the random packing densities 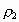 and
and 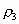 for 2D and 3D spheres,
respectively, in the limit for 2D and 3D spheres,
respectively, in the limit 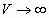 by
using CPA. Their estimates are by
using CPA. Their estimates are 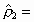 0.5474 0.5474 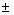 0.0003
(95% int.) and 0.0003
(95% int.) and 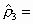 0.3809 0.3809 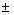 0.0007
(95% int.), respectively. These values are comparable with those listed
in Evans (1993). 0.0007
(95% int.), respectively. These values are comparable with those listed
in Evans (1993).
The extension of CPA to higher dimensions is straightforward in principle.
By using the computer programs for higher dimensional Voronoi tessellation
used in Tanemura (2001), it is desirable to perform computer simulations
of random sequential packing of 4D and 5D spheres.
References
Evans, J.W. (1993) Random and cooperative sequential
adsorption: Reviews of Modern Physics, 65, 1281-1329.
Palásti, I. (1960) On some random space filling
problem: Publications of Mathematical Institute of Hungarian Academy
of Sciences, 5, 353-359.
Rényi, A. (1958) On a one-dimensional problem concerning
random space-filling: Publications of Mathematical Institute of Hungarian
Academy of Sciences, 3, 109-127.
Solomon, H. and Weiner, H. (1986) A review of the packing
problem: Communications in Statistics and Theoretical Methods, 15,
2571-2607.
Tanemura, M. (1979) On random complete packing by discs:
Annals
of the Institute of Statistical Mathematics, B31, 351-365.
Tanemura, M. (1981) On random complete parking of spheres
in 2D and 3D spaces: Proceedings of the International Roundtable Congress.
50-th Anniversary of Japan Statistical Society, 216-229.
Tanemura, M. (1988a) Random packing and random tessellation
in relation to the dimension of space: Journal of Microscopy, 151,
247-255.
Tanemura, M. (1988b) On the density of strict random complete
parking by discs: Research Memorandum, The Institute of Statistical
Mathematics, 339, 1-24.
Tanemura, M. (2001) Random Voronoi cells of higher dimensions:
Symmetry:
Art and Science, 1-2, 186-189.

|
