|
SELF-REVERSED CONFIGURATIONS
ON CUBE
Y. TESHIMA, K. KASE, S. Usami,
M. KATO, N. IKEDA, and A. Makinouchi
|
Name: Yoshinori Teshima, (b.
Hikosan, Fukuoka, Japan, 1970).
Address:Integrated
VCAD System Research Program, RIKEN (The Institute of Physical and Chemical
Research), Wako, Saitama 351-0198, Japan. E-mail: kippoh@riken.jp
Fields
of interest: Geometry, combinatorics, mathematical crystallography,
statistical physics.
Awards:The
Prize for an Excellent Research Paper with Encouragement (10th Award of
the Society for Science on Form), 2004.
Publications
and/or Exhibitions: Y. Teshima and T. Ogawa (2000) Dense packing
of equal circles on a sphere by the Minimum-Zenith Method, Forma, Vol.15,
pp. 347-364. Y. Teshima Y. Watanabe, and T. Ogawa (2001) A new structure
of cylinder packing, Lecture Notes in Computer Science (Springer), LNCS-2098,
pp. 351-361. Y. Teshima, K. Kase, S. Usami, N. Ikeda, and A. Makinouchi
(2004) Enumeration of cutting points configuration in cube cutting", to
appear in proceedings of HART2004, Univ. of Fukui, Japan.
|
| Abstract: The number of patterns
for painting six faces, eight vertices, and 12 edges of a cube with two
colors black and white is shown respectively. At first, we considered symmetry
as only the rotation of the cube, but then added the reflection in the
cube, and finally the interchange of the two colors. Such interchange distinguishes
only contrast of colors. If the interchange maintains the same contrast,
we call it "self-reversed configuration". We counted the number of self-reversed
configurations in cube coloring, and found that there are two self-reversed
configurations in face coloring, six self-reversed configurations in vertex
coloring, and eight self-reversed configurations in edge coloring. |
1 ENUMERATION IN COMBINATORIAL MATHEMATICS
Enumeration in combinatorial mathematics is important in modern science
and technology. For example, it was applied in physics (Mayer and Mayer
1940), chemistry (Pólya 1937), information science (Harrison 1965),
computer graphics (Lorensen and Cline 1987), etc. .
Recently, the authors investigated the enumeration of cutting point
configurations in cube cutting (Teshima et al. 2004), which provided the
mathematical foundation of Volume CAD (VCAD) as a next generation computer-aided
design (CAD) tool (Kase et al. 2003). The enumeration process involved
was equivalent to finding the distinct ways of painting the twelve edges
of a cube with two colors.
In this short paper, enumerations for painting six faces, eight vertices,
and 12 edges of a cube with two colors are described in Section 1.1, and
"self-reversed configuration" is discussed in Section 2.
1.1 Painting cube with two colors
We summarized how many equivalent classes (= patterns) there are when
we paint six faces, eight vertices, and 12 edges of a cube using two colors
black and white. If the symmetry of the cube were not taken into account,
there were 26=64 different configurations
altogether for face coloring, 28=256 different configurations
altogether for vertex coloring, and 212=4096 different configurations
altogether for edge coloring. We considered both symmetric group the rotation
group and reflection group of a cube. We calculated the number of patterns
in all configurations using the Pólya's theory of counting (Redfield
1927 and Pólya 1937), which is useful for enumeration under group
action. In most applications of the Pólya theory, only the rotation
group is considered and then enantiomorphous pairs which are mirror images
of each other are counted individually. However, from the standpoint of
pure geometry or pure group theory, such distinction is superfluous and
it is proper to add the reflection group for reducing them (Coxeter 1989).
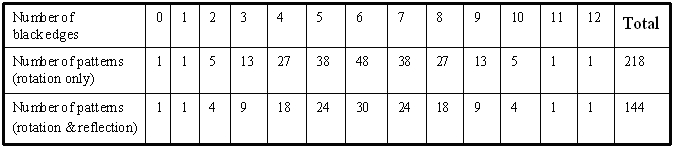
Enumeration results are shown in Table 1, 2, and 3. The second row in
the tables shows the number of patterns under the rotation group only,
and the third row shows the number of patterns under both the rotation
and reflection groups. On face coloring, all 64 configurations are classified
into 10 patterns, all 256 configurations are classified into 23 or 22 patterns
on vertices coloring, and all 4096 configurations are classified into 218
or 144 patterns on edge coloring.
Table 1: Number of patterns for painting six faces of cube using black
and white Enumeration results under both rotation and reflection
groups are the same as the number under the rotation group
because enantiomorphous pairs do not appear in face coloring.
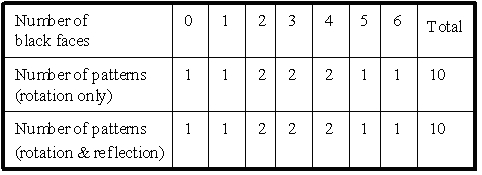
Table 2: Number of patterns for painting eight vertices of cube using
black and white

Table 3: Number of patterns for painting 12 edges of cube using black
and white
2 SELF-REVERSED CONFIGURATION
When interested only in the contrast patterns in Table 1, 2, and 3,
we further reduce the total number of patterns. In face coloring, for example,
in the case of (number of black faces, number of white faces) = (0, 6),
(1, 5), and (2, 4), their contrast patterns are the same as the cases:
(6, 0), (5, 1), and (4, 2). Thus, the former patterns can be reversed into
the latter patterns. Here, "reverse" means the interchange of the two colors
black and white. We need careful judgment for two patterns in the case
of (3, 3) in Table 1. The same situation occurs in vertex coloring and
edge coloring. We must judge six patterns in the case of (number of black
vertices, number of white vertices) = (4, 4) in Table 2, and 30 patterns
in the case of (number of black edges, number of white edges) = (6, 6)
in Table 3.
As a result, each of the two patterns of (3, 3) in face coloring is
self-reversed configuration, and each of the six patterns of (4, 4) in
vertex coloring is also self-reversed configuration. Concerning the 30
patterns of (6, 6) in edge coloring, only eight patterns are self-reversed
configurations and the other 11 patterns are reversed into the remaining
11 patterns. Figure 1, 2, and 3 show these results. The index with an underline
shows that the figure is self-reversed. (And the index with an asterisk
in the figures shows that the figure is one of the enantiomorphous pairs.)
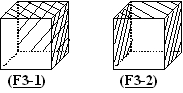
Figure 1(above): Two contrast patterns of (3,3) in face coloring
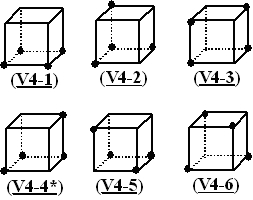
Figure 2(right): Six contrast patterns of (4,4) in vertex coloring
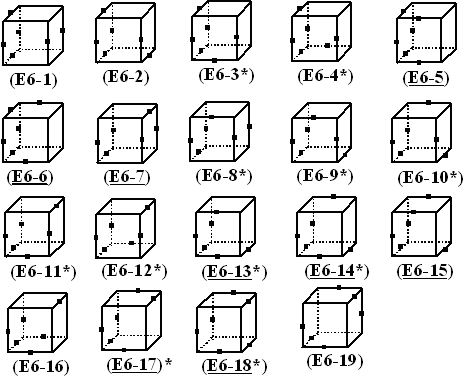
Figure 3: Nineteen contrast patterns of (6,6) in edge coloring.
Only eight figures with underlined index are self-reversed.
References
Coxeter, H. S. M. (1989) Introduction to Geometry,
Second edition, Section 15.6, New York: Wiley.
Harrison, M. A. (1965) Introduction to Switching
and Automata theory, New York: McGraw Hill Book Company.
Kase, K., Teshima, Y., Usami, S., Ohmori, H., Teodosiu,
C., and Makinouchi, A. (2003) Volume CAD, Proceedings of the 3rd International
Workshop on Volume Graphics (VG03), 145-150 and 173.
Lorensen, W. E. and Cline, H. E., (1987) Marching cubes:
A high resolution 3D surface construction algorithm, Computer Graphics
(SIGGRAPH 87 Conference Proceedings), 21(4), 163-169.
Mayer, J. E. and Mayer, M. G. (1940) Statistical Mechanics,
New York: Wiley.
Pólya,
G. (1937) Kombinatorische Anzahlbestimmungen fur Gruppen, Graphen, und
chemische Verbindungen, Acta Math., 68,145-254.
Redfield, J. H. (1927) The theory of group reduced distributions,
Amer.
J. Math.,49, 433-455.
Teshima, Y., Kase, K., Usami, S., Kato, M., Ikeda, N.,
and Makinouchi, A. (2004) Enumeration of Cutting Points Configuration in
Cube Cutting, to appear in proceedings of HART2004, Univ. of Fukui, Japan.

|