Rational particle systems are made from three, two or one dimensional grids of rational points programmed to flow in three dimensional space. These points are coloured according to their lowest common denominator in an initial reference position. In the first image below, a three dimensional grid of rational points is flowing within a unit cube. Each orthogonal direction is assigned a different frequency. Observable alignments of particles of related denominators (for example multiples of six) form as a result of the quotient map 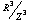. In other words, particles disappearing out one side of the cube immediately re-enter from the opposite face where they overlap with previous layers of the particle system.

In the second image, a two dimensional grid of rational points are programmed to flow in a spiralling torus or doughnut shape. The longitudinal and meridian flows are assigned different frequencies. This time the quotient map 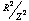 is staggered off the surface of the torus into a volume. This allows for the formation of extended spatial alignments as flowtime increases. Locally, these alignments spiral as they coalesce and dissipate. Globally, this object resembles a swirling galaxy. In the third image, numerous one dimensional grids of rational points are programmed to flow in and around the surface of a sphere. The flow is two dimensional (with two different orthogonal frequencies), however the objects are initially one dimensional. The result is an ever-changing visually complex particle system in which alignments possessing great symmetry continually coalesce in and out of existence. Two examples of instantaneous symmetrical alignments are shown in the fourth image.  As humans we recognise these alignments as visual events in an otherwise chaotic flow.