|
DEVELOPMENT OF THE FUNDAMENTAL
DMITRY WEISE
1 FUNDAMENTAL THEOREM OF THE PHYLLOTAXIS The Fundamental Theorem of the Phyllotaxis (called so by Roger V. Jean) is understood as a number of the statements concerning interrelation of a divergence angle with parastichy number on families of a spiral phyllotaxis pattern. Key items of these statements are formulas that describe normal (for additive Fibonacci type series, starting with U1=1) and anomalous (for the additive series starting only with U1=2) phyllotaxis. Cases when U1=>3 were been named aberrant and problematic patterns. 1.1 Glossary Phyllotaxis: The arrangement of leaf or floret primordia at the shoot apex, or on the stem. In 92% of the observation the contact on conspicuous parastichy pair (m, n) in phyllotactic patterns is such that m and n are consecutive terms of the Fibonacci sequence, and the divergence angle d converges rapidly toward the Fibonacci angle. When m and n do not belong to the Fibonacci sequence, they are generally consecutive terms of a Fibonacci-type sequence. This constitutes a part of the challenge of phyllotaxis.
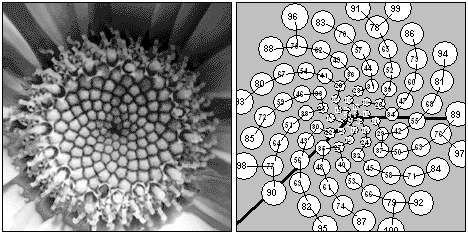
Figure 1: Daisy florets are arranged in a pattern of sets
of parastichies,
F1 = 1 ; F2 = 1; á 1, 1, 2, 3, 5, 8, 13, 21…ñ ; D = 222.5°; d = – 137.5°. |D| + |d| = 360° In new terms: s = 1; t = 2; U1 = s; U2 = st – 1. Fibonacci sequence: The sequence of integers: 1, 1, 2, 3, 5, 8, 13, … The kth term is built using the rule Fk = Fk-2 + Fk-2 from the initial values F1=1; F2=1. Fibonacci-type sequence: A sequence built from the same recurrence rule as the Fibonacci sequence but starting with other initial terms. For example, Lucas sequence: 1, 3, 4, 7, 11, 18, 29, 47, …; Uk = Uk-2 + Uk-1 ; U1 , U2 – integers ; n = 1, 2, 3, … Golden ratio: a =(1+Ö 5)/2=1.6180339…; b =(1–Ö 5)/2 = –0.6180339…; t = a ; t–1 = –b . Divergence angle d: Any of the two angles at the center of a transverse section of a growing shoot tip determined by consecutively initiated primordia. (This definition differs from those, given by Roger V. Jean, a little). Fibonacci angle: The divergence angle d =360*t–1 ? 137.5° or D=360*(1– t–1 ) ? 222.5° Parastichy: Any phyllotactic spiral seen on plants, or in transverse sections of plant apices. If along a parastichy the numbers differ by n then we say that it is a n-parastichy. Family of parastichies: Given any parastichy in the centric
representation, the corresponding family is the set of parastichies with
the same pitch, winding around a common pole in the same direction and
going through the centers of all the primordia.
2 RESULTS - PREDECESSORS
where t ³ 2 is an integer By R. V. Jean
(1994, pp. 37-38)
3 NEW RESULTS
where s and t are integers Notice that on figures in central area the circles are not evenly distributed, but in the outer part a packing become denser. By analogy, a ratio of two consecutive Fibonacci-type numbers Uk and Uk+1 approaches Golden ratio as k become large.
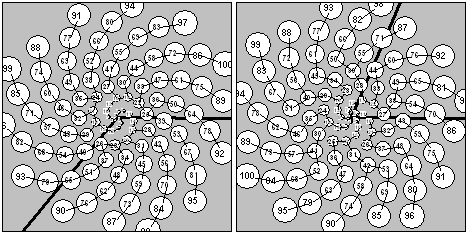
Figure 2: (a) s = 3; t= 4; U1
= s = 3 ; U2 = st – 1 = 11; U3 = 14; d=–129.34°;
D=230.66°
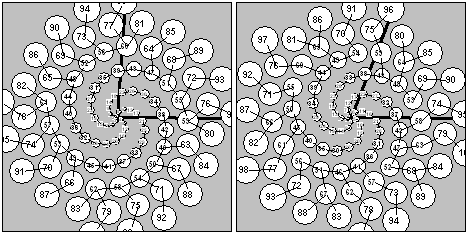
a b Figure 3: (a) s = 4; t= 4; U1 = s =
4 ; U2 = st + 1 = 17; U3 = 21; d = 85.38°; D=–274.62°
|
||||||||||||||||||||||||||||||||