|
PYTHAGOREAN APPROACH TO PROBLEMS OF PERIODICITY IN FERMIONIC SYSTEM DMITRY WEISE
1 INTRODUCTION Structural similarities exist between atomic nuclei and other fermionic system such as metal clusters. In particular both of these systems exhibit specific magic numbers. 1.1 Figurate numbers, gnomon, and Pascal’s triangle Figurate or polygonal numbers appeared in 15th-century arithmetic books, and were probably known to ancient Chinese; but they were of particular interest to ancient Greek mathematicians. To the Pythagoreans (c. 500 BC), numbers were of paramount significance: they believed everything could be explained by numbers, and numbers were invested with specific characteristics and "personalities". Among the properties of numbers the Pythagoreans endowed them with "shapes" The connotation of the term gnomon is that originally given by Hero
of Alexandria, namely, 'A Gnomon is that form that, when added to some
form, results in a new form similar to the original.'
2 PERIODICITY OF ATOMIC PROPERTIES In the atomic shell model, the shells are filled with electrons in order of increasing energy until they fill a closed shell, producing the inert core of noble gases. The atomic magic numbers 2, 10, 18, 36, 54, 86, correspond to the total number of electrons in filled shells.
Figure 1: On the left – figurate number
218 – 3D Mendeleyev's periodic system.
The manipulations performed with Pascal's triangle and figurate numbers result in a 3D model for Mendeleyev's periodic system, to which one may give the interpretation submitted in Figure 1. The figurate-numerical approach yields an algebraic expression for the atomic numbers of inert gases: Z = [ (-1)n (3n + 6) + 2n3 + 12n2 + 25n - 6 ] / 12, (1) where n = 1, 2, 3, ... is the period number.
3 PERIODICITY OF NUCLEAR PROPERTIES
Figure 2: On the left – figurate number
126.
Since Pascal’s triangle has proven successful in determining atomic magic numbers, the question arises as to whether it can also help to identify nuclear magic numbers – can it provide a geometrical image and an analytical formula just as for atoms? The magic numbers for nuclei are: 2, 8, 20, 28, 50, 82, 126, corresponding to the total numbers of protons and neutrons in filled nuclear shells. Nuclei with magic numbers of protons and neutrons are unusually stable. A formula valid for all the nuclear magic numbers is: MNm= k* (m2 - m) + (m3 + 5m)/3, (2) where m = 1, 2, 3, ... with k = 1 if m=1, 2,3;
k
= 0 if m > 3.
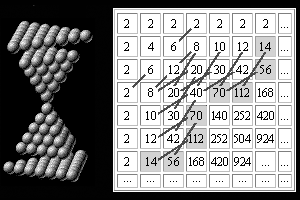
4 PERIODICITY OF CLUSTERS PROPERTIES The Pythagorean approach can be applied to the discovery of magic numbers in the analysis of stability properties of clusters formed by inert-gas or alkali-metal atoms. Let's consider application of the Pythagorean approach for the analysis of one of magic numbers sequences: 7, 29, 66, 118 and 185. The method of finite differences can sometimes be used to guess a formula f(n) (but not to prove it). Application of Pascal’s triangle means use of a method of finite differences. In terms of Pythagorean school it is possible to tell: if the method of finite differences is applicable, each difference can be considered as gnomon for an above row. Table 1 - Pascal's triangle modification "C".
Explicit form: Cn = (15n2 - n )/ 2 , where n = 1, 2, 3,… (3) CONCLUSION In this paper we have shown an attempt to couple modern atomic theories
with an ancient scientific guiding principle. In particular, a parallel
between atomic and nuclear shells and such a fundamental concept of the
Pythagorean school known as the gnomonis carried out.
References Ladma V. Magic numbers. http://www.sweb.cz/vladimir_ladma/english/notes/texts/magicn.htm Pythagoras and the Pythagoreans, http://www.math.tamu.edu/~don.allen/history/pythag/pythag.html Weise, D. The Pythagorean approach to the problems of periodicity in chemistry and nuclear physics, In: Progress in Theoretical Chemistry and Physics, Vol. 12, Advanced Topics in Theoretical Chemical Physics, Edited by Jean Maruany, Roland Lefebvre, and Erkki J. Brändas, 459-477. ISBN 1-4020-1564-X
|