Live3D Animations to Solution of Conway-Radin-Sadun Problem


Izidor Hafner
Faculty of Electrical Engineering, University of Ljubljana
Trzaska 25, 1000 Ljubljana, Slovenia
e-mail: izidor.hafner@fe.uni-lj.si

Abstract. For each non-snub Archimedean solid with icosahedral symmetry we construct its best “rhombic approximate”. By rhombic solid we mean a polyhedron that consists of prolate and oblate golden rhombohedra. In the solution we also use halves of rhombic dodecahedron of the second kind, which in turn consists of two halves of the rhombohedra. Some combinations of Archimedean solids are equidecomposable to some combinations of their approximates, and can be dissected to a cube.

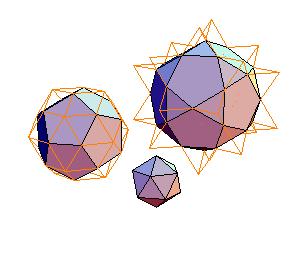
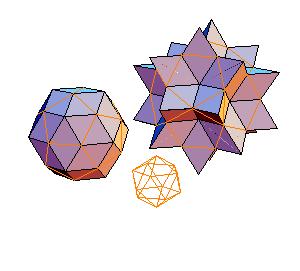
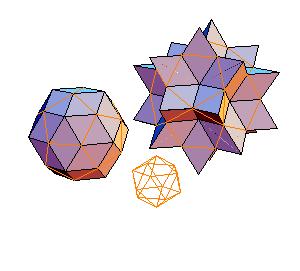
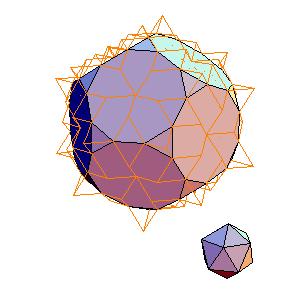
Introduction

In 1900 Max Dehn showed that it was impossible to cut a regular tetrahedron into finitely many pieces by planes and paste the pieces into a cube (Hilbert's third problem) by giving a necessary condition for the mutual equidecomposability of polyhedra. In 1938 H. Lebesque proved that no two Platonic polyhedra were equidecomposable. In 1965 J.P. Sydler proved that Dehn's criterion is also sufficient [1]. In [2] J. H. Conway, C. Radin and L. Sadun applied their theory of geodetic angles to the non-snub Archimedean polyhedra proving that some combinations of Platonic and Archimedean solids can be decomposed to a cube. In particular it was proved [2] that it was possible to dissect the icosahedron, dodecahedron, and icosidodecahedron into finitely many pieces that can be reassembled to form a large cube. The problem is, how to perform such dissection. The authors of [2, pg. 331] produced the table of the Dehn invariants for the non-snub unit edge Archimedean polyhedra.


It follows that the following combinations with sum 0 exist:


Truncated icosidodecahedron
Icosahedron+ Truncated dodecahedron
Dodecahedron+ Truncated icosahedron
Icosahedron+ Dodecahedron+ Icosidodecahedron
Icosidodecahedron+ Rhombicosidodecahedron
Truncated icosahedron+ Truncated dodecahedron+ Rhombicosidodecahedron


For each of the above combinations we found an equidecomposable combination of rhombic solids. In fact there are basically two solutions depending on the length of edges of the Archimedean solid, which may be shorter or larger diagonal of the rhombus.


1. Equidecomposable combinations, edge equals smaller diagonal

1. Icosahedron + dodecahedron + icosidodecahedron

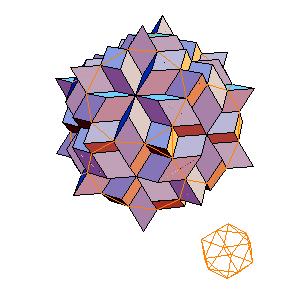
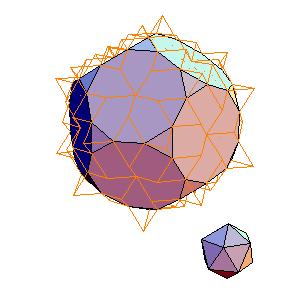
2. Icosahedron + truncated dodecahedron

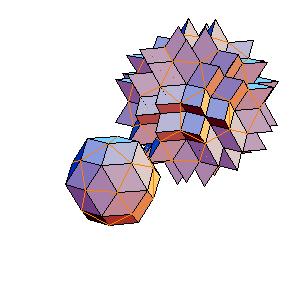
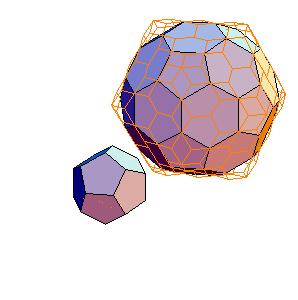
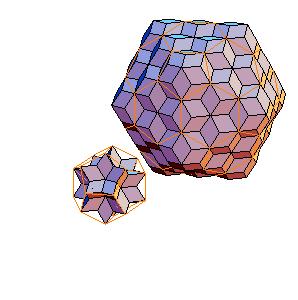
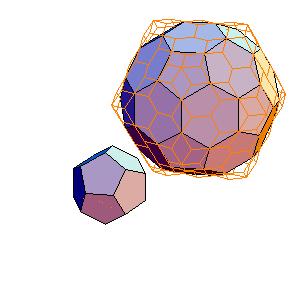
3. Dodecahedron + truncated icosahedron

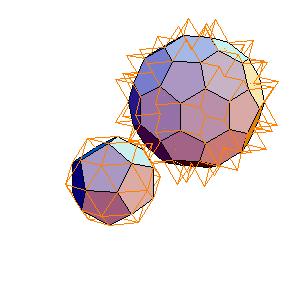
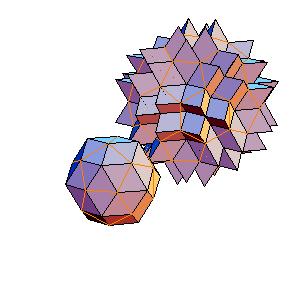
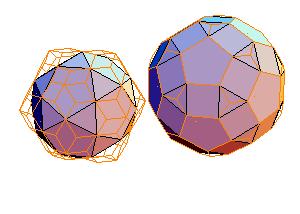
4. Icosidodecahedron + rhombicosidodecahedron

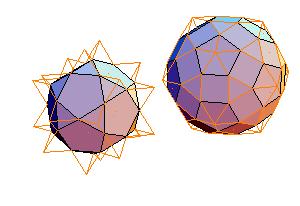
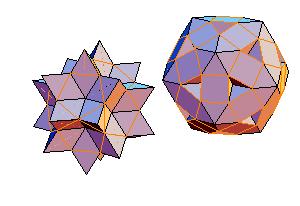
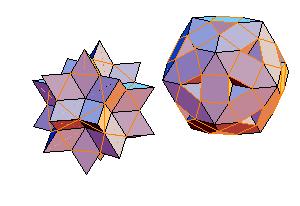
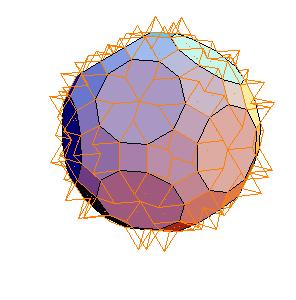
5. Truncated icosahedron + truncated dodecahedron + rhombicosidodecahedron

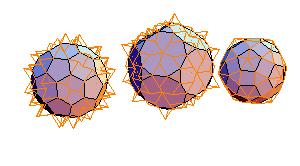
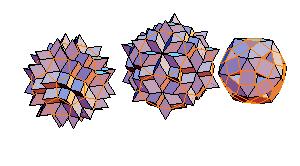
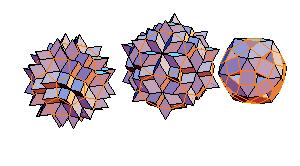
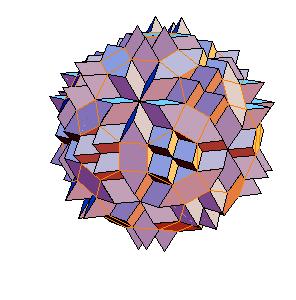
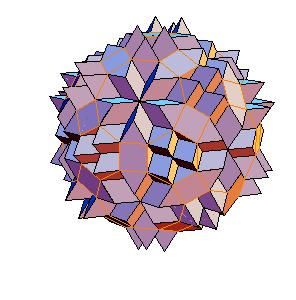
6. Truncated icosidodecahedron


2. Equidecomposable combinations, edge equals larger diagonal

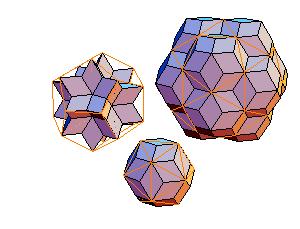
1. Icosahedron + dodecahedron + icosidodecahedron

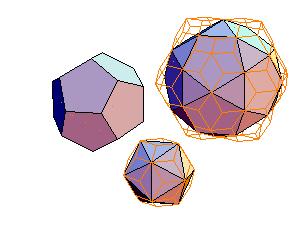
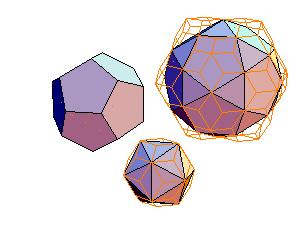
2. Icosahedron + truncated dodecahedron

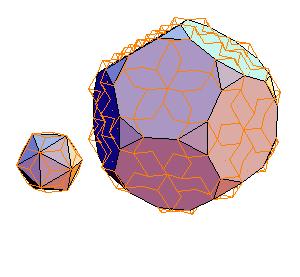
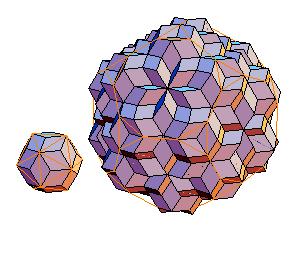
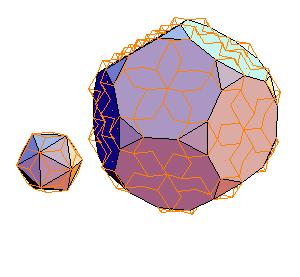
3. Dodecahedron + truncated icosahedron

4. Icosidodecahedron + rhombicosidodecahedron

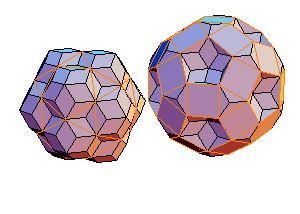
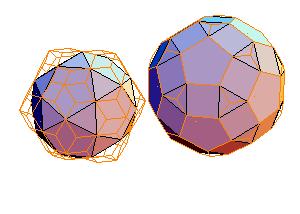
5. Truncated icosahedron + truncated dodecahedron + rhombicosidodecahedron

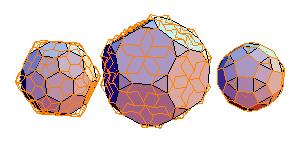
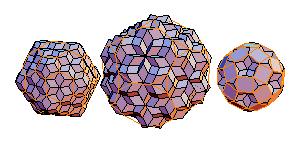
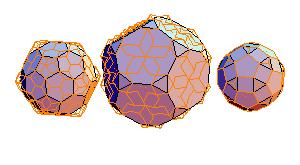
6. Truncated icosidodecahedron

References


[1] V.G. Boltjanskii, Tretja problema Hilberta, Nauka, Moskva 1977.
[2] J. H. Conway, C. Radin, and L. Sadun, On angles whose squared trigonometric functions are rational, Discrete & Computational Geometry, 22 (1999), pages 321-332.
[3] P. R. Cromwell, Polyhedra, Cambridge U. Pr., 1997
[4] G. N. Frederickson, Dissections: Plane & Fancy, Cambridge U. Press, 1997.
[5] I. Hafner, T. Zitko, A dissection of quarter of rhombic dodecahedron of the second kind to a cube, http://torina.fe.uni-lj.si/~izidor/RhombicPolyhedra/RhombicPolyhedra.html
[6] I. Hafner, T. Zitko, Introduction to golden rhombic polyhedra - published in Visual Mathematics Vol.4, No.2, 2002, 2, (3)
[7] I. Hafner, T. Zitko, Relations among rhombic, Platonic and Archimedean solids - published in Visual Mathematics Vol.4, No.2, 2002, 2, (4)
[8] I. Hafner, B. Jurcic-Zlobec, T. Zitko, Gallery of rhombic polyhedra, - published in Visual Mathematics Vol.4, No.2, 2002, 2, (4)
[9] Martin Kraus' Live3D applet http://www.vis.uni-stuttgart.de/~kraus/index.html