Some patterns using specific tiles

John Rigby, Brian Wichmann

1  Introduction

Islamic patterns often consist of braids interlacing each other, usually in an under-over manner (Figure 1, a recently devised pattern named after the modern London landmark which it resembles. See also the figures eye,eye2). For the purposes of recording the basic geometrical properties of such a pattern, the braiding can be reduced to a single line (Figure 2). This is done in collections of patterns dating back as far as the 15th century, for example The Topkapi Scroll [5], as well as in more modern publications ([3,2,4]). Figure 3 shows a pattern from [5] with colouring added. Sometimes this skeletal form of a pattern occurs in actual ceramic wall tilings; this happens in Spain, but may be less common in other Islamic countries. The four polygonal shapes of tile to be discussed here occur frequently in patterns (some very elaborate) involving 10-pointed stars or 10-petalled rosettes; Figure 3 shows one example, and many more occur in [2] and [3], but there is no example in [2] or [3] involving only these four shapes and no others. Yet they can be used on their own, as in Figure 4, to create many fascinating periodic tiling patterns; the number of such patterns, even if restrictions are imposed, is so large that any systematic enumeration presents insurmountable problems, so we shall just present a few aspects of the topic, arising from our shared enjoyment of the creation of patterns.
Figure 1: Tiling with braiding (the London Eye)
Figure 2: The corresponding tiling without braiding
Figure 3: From the Topkapi Scroll
One of the shapes - the regular pentagon - is of particular interest. It occurs frequently in Islamic art, and is the ultimate source of the golden ratio. A rotation of order 5 does not occur in any of the seventeen plane symmetry groups, but that does not prevent regular pentagons from being used in many periodic patterns.
In our illustrations the pentagons will always be coloured blue. The other tiles in our set are a white eight-sided figure, which always occurs in conjunction with two small olive kites to form a large diamond, and a brown ten-sided figure. We shall refer to these shapes as 4-gons (the olive kites), 8-gons and 10-gons even though they look very different from the regular polygons with the same names. The angles in all the tiles are equal to 72°, 108°, 144°, 216° and 252°.
Figure 4: Example of tiling with the chosen prototiles

2  A theorem

Since an 8-gon is always adjacent to two 4-gons, we know that in any pattern there will always be twice as many 4-gons as 8-gons.
Define a period parallelogram (see [1]) or unit cell of a periodic pattern as a parallelogram of minimum area placed onto a tiling pattern such that when the parallelogram is repeated by translation to cover the plane, the pattern underneath each parallelogram is the same. As an example, in Figure 5 we have redrawn the pattern of Figure 4 in outline. The unit cells have been drawn by means of lines joining the upper right-hand vertices of the 10-gons.
Figure 5: Tiling showing unit cell
We shall now prove that in a unit cell of any periodic tiling using only our four types of tile, there are twice as many pentagons as 10-gons. The same is therefore true in any fundamental region, since a unit cell is made up of fundamental regions.
A unit cell contains an integral number of tiles of each type (if part of a tile is cut off by an edge of the cell, then part of another tile, identical in size, shape and orientation to the part cut off, appears along the opposite edge of the cell). We shall count up the number of corners of the tiles within a unit cell, and to this end we first translate the unit cells slightly so that no vertex of the pattern lies on a bounding line of any cell. It is convenient to regard each 8-gon with its two attendant 4-gons as a single rhombus with eight edges and eight corners, the angle at four of the corners being a straight angle. The edges inside each rhombus, common to the 4- and 8-gons, are to be deleted or ignored. We take the number of rhombi inside a unit cell as r, the number of pentagons as p and the number of 10-gons as q. There are four types of corner in the cells - acute, obtuse, re-entrant and straight. There are four types of vertex in the pattern, denoted by the letters A, B, C and D as follows:
A:
Two acute and two obtuse corners meet.
B:
One acute and one obtuse and one straight corner meet.
C:
One obtuse and one re-entrant corner meet.
D:
Two straight corners meet.
Figure 6: Unit cell showing vertex types
In our example, the four types of vertex are shown in Figure 6. We take the number of A vertices in the unit cell as a, and similarly for b, c and d.
We shall now count the number of corners inside a unit cell in two ways. We can use the counts of vertex types (a, b, c and d), or the counts of the tiles (r, p and q). Hence we have the numbers of each corner type as follows:
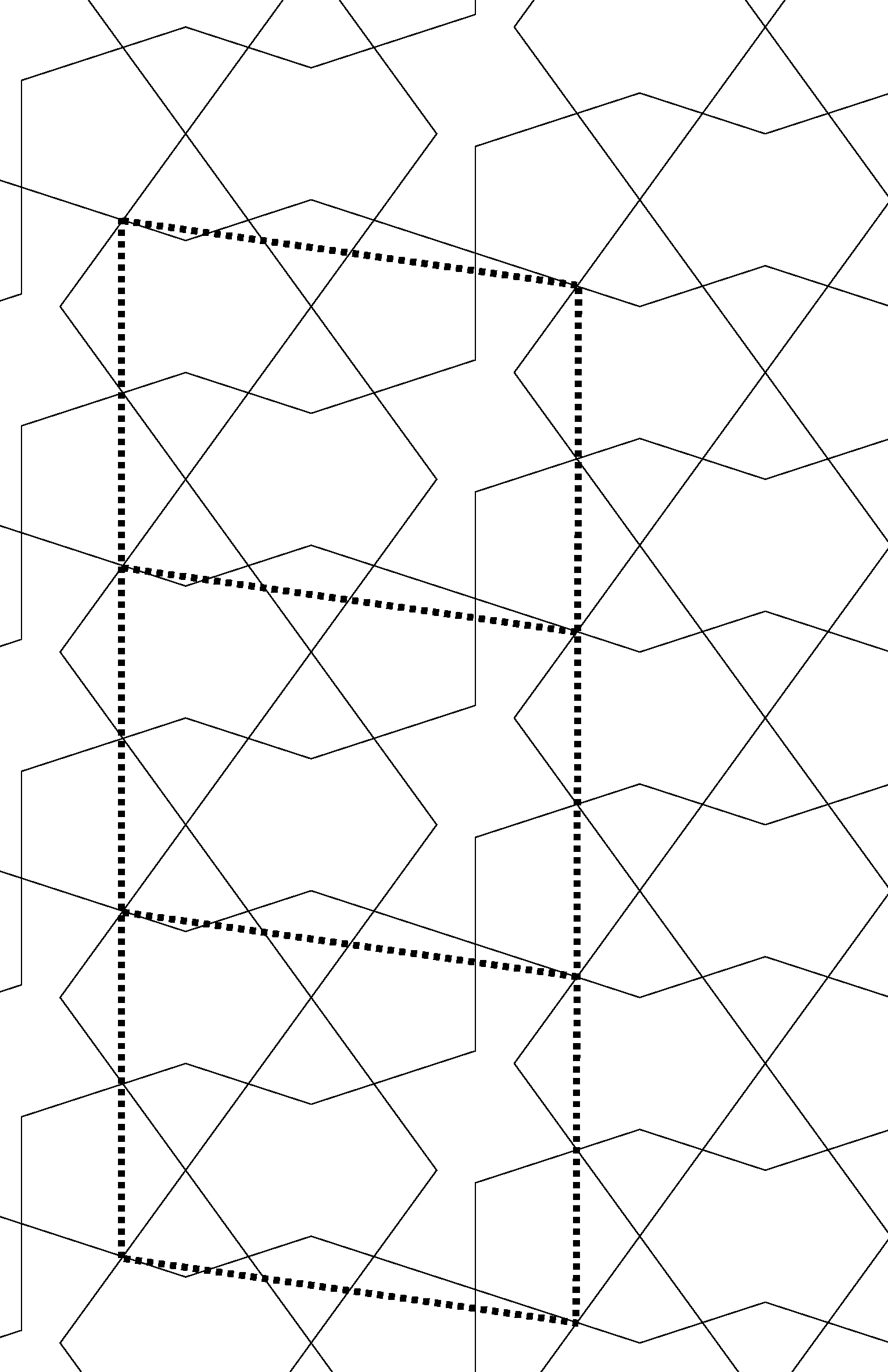
acute corners 2a + b = 2r + 6q (1)
obtuse corners 2a + b + c = 2r + 5p (2)
re-entrant cornersc = 4q (3)
straight corners b + 2d = 4r (4)
Subtracting (1) from (2) gives c = 5p - 6q; hence using (3), 5p - 6q = 4q so p = 2q as required.
Finally we can observe that a tiling pattern can be produced with any ratio of r to q. One simply replicates the appropriate number of strips of rhombi and strips of pentagons and 10-gons as shown in the tiling TRY21.

3  Some examples

Some of the patterns we have constructed are listed in Table 1. We now have one major characteristic of the periodic patterns being studied: the number of 8-gons and the number of 10-gons in a fundamental region. The notation used in the table is as follows:
Figure 7: The four types of 10-gon
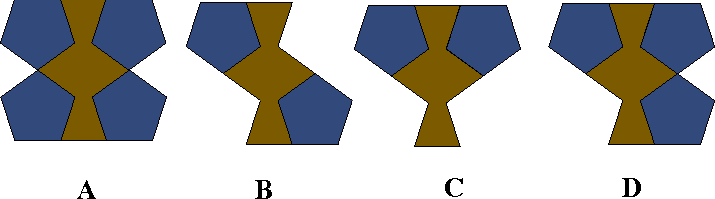
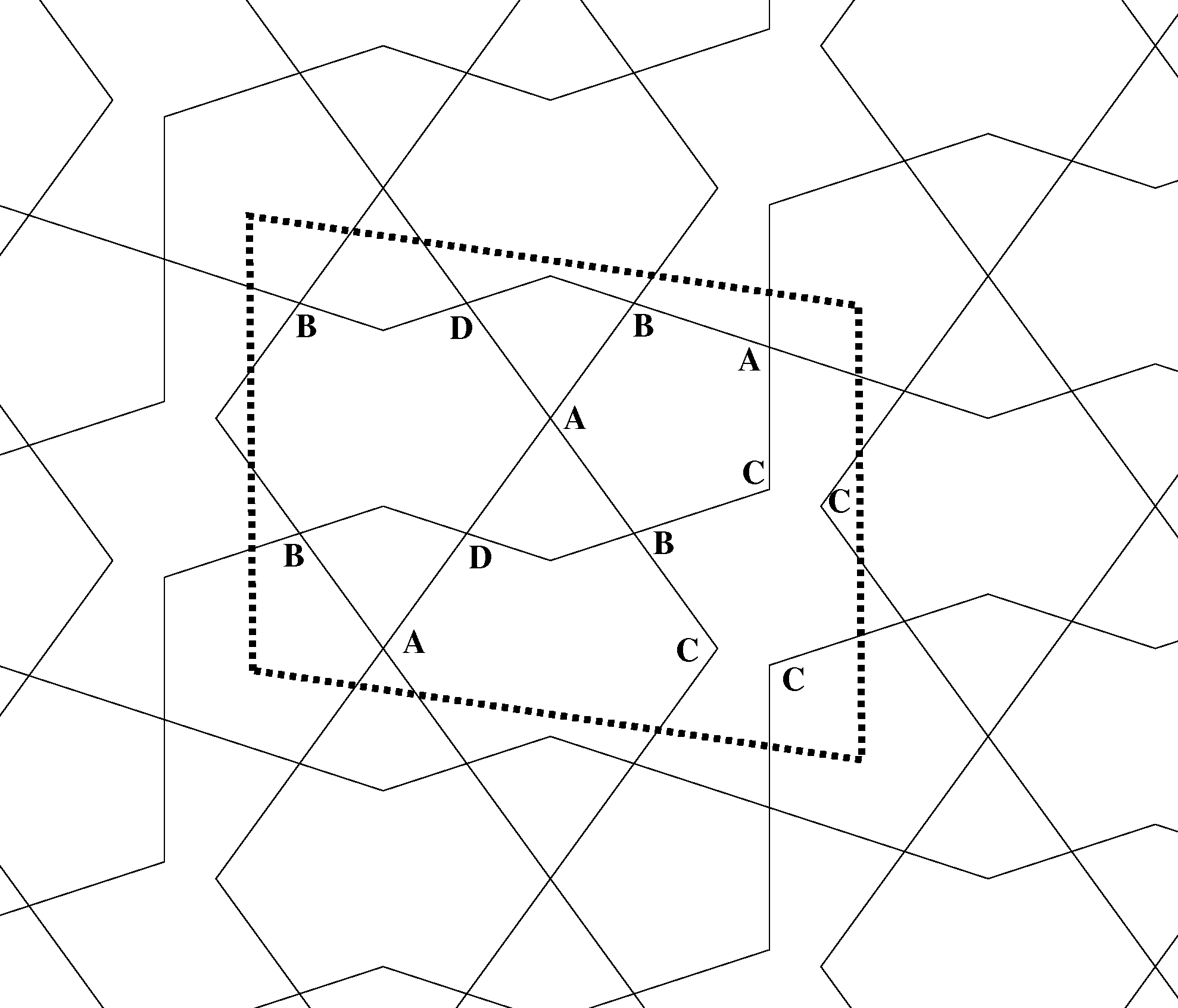
Symmetry 8-gon 10-gon Interlacing Name
cm [ 1/2], 1 1, 2, D 0,3 TRY54
cm 1, 2 [ 3/2], 3, BD 1,0 TRY43
cm [ 3/2], 3 1, 2, B 1,0 TRY42
cm [ 3/2], 3 [ 5/2], 5, ACD 1,0 TRY46
cm 2, 3 2, 4, DD 1,1 TRY37
cm 2, 3 4, 5, AACD 2,1 TRY60
cm 2, 3 4, 5, AACD 1,1 TRY62
cmm [ 1/4], 1 [ 3/4], 3, AA 1,1 TRY80
cmm [ 1/2], 1 [ 3/4], 3, AB 1,1 TRY16
cmm [ 1/2], 1 [ 5/4], 3, AAB 3,0 TRY26
cmm 1, 1 [ 5/4], 3, AA 1,2 TRY78
cmm [ 3/2], 3 [ 9/4], 5, AD 3,0 TRY79
cmm 2, 3 4, 5, AACD 4,0 TRY68
cmm 2, 3 4, 5, AACD 3,2 TRY69
cmm 2, 3 4, 5, AACD 3,0 TRY70
cmm 2, 3 4, 5, AACD 3,1 TRY71
p1 2, 2 2, 2, BD 0,2 TRY39
p1 2, 2 4, 4, AACD 0,1 TRY48
p2 [ 1/2], 1 [ 1/2], 1, B 0,2 TRY22
p2 [ 1/2], 1 [ 1/2], 1, A 0,3 TRY20
p2 1, 1 [ 1/2], 1, B 0,2 TRY34
p2 1, 2 [ 1/2], 1, B 0,1 TRY08
p2 1, 2 1, 1, D 0,2 TRY55
p2 1, 2 [ 3/2], 2, AC 0,1 TRY02
p2 [ 3/2], 2 [ 1/2], 1, B 0,2 TRY52
p2 [ 3/2], 2 [ 3/2], 3, AB 1,0 TRY04
p2 2, 2 [ 1/2], 1, B 0,3 TRY07
p2 2, 2 [ 1/2], 1, B 0,2 TRY53
p2 2, 2 4, 4, AACD 3,1 TRY49
p2 2, 2 4, 4, AACD 1,2 TRY58
p2 2, 2 4, 4, AACD 1,2 TRY61
p2 3, 3 4, 3, ACCD 2,2 TRY09
p2 3, 3 4, 3, ABCC 2,1 TRY03
pg 1, 1 1, 2, D 0,3 TRY40
pg 1, 2 1, 1, A 0,4 TRY41
pg 2, 3 4, 5, AACD 0,1 TRY56
pg 2, 3 4, 5, AACD 0,2 TRY59
pgg [ 1/2], 2 [ 1/2], 2, B 1,0 TRY00
pgg [ 1/2], 2 1, 1, A 0,2 TRY06
pgg 1, 2 [ 1/2], 2, B 0,2 TRY25
pgg 2, 3 4, 5, AACD 1,2 TRY64
pgg 2, 3 4, 5, AACD 1,1 TRY67
pgg 2, 3 4, 5, AACD 0,2 TRY76
pm 2, 3 2, 4, BD 0,3 TRY36
pm 2, 3 3, 5, ABDD 1,1 TRY45
pm 2, 3 4, 5, AACD 3,0 TRY51
pm 2, 3 4, 5, AACD 1,1 TRY57
pmg [ 1/2], 1 [ 1/2], 2, B 0,3 TRY23
pmg [ 1/2], 1 1, 3, AB 0,2 TRY77
pmg [ 1/2], 2 [ 1/2], 1, A 0,2 TRY21
pmg 1, 3 [ 1/2], 2, B 0,1 TRY35
pmg 1, 1 [ 3/2], 3, AB 0,4 TRY27
pmg 2, 3 4, 5, AACD 3,0 TRY65
pmg 2, 3 4, 5, AACD 3,0 TRY63
pmg 2, 3 4, 5, AACD 2,2 TRY72
pmg 2, 3 4, 5, AACD 3,0 TRY73
pmg 2, 3 4, 5, AACD 1,2 TRY74
pmg 2, 3 4, 5, AACD 1,2 TRY75
pmg 3, 3 4, 3, AABC 2,1 TRY14
pmm 1, 1 [ 3/2], 3, AAB 1,1 TRY38
pmm 2, 3 4, 5, AACD 5,0 TRY50
Table 1: List of tilings (All)

4  An analysis of areas

Let us suppose that the pentagons have edge-length 1. Then a 10-gon and two pentagons together have area 4tsin72° (Figure 7B), where t is the golden number, and a rhombus (an 8-gon and two small kites) has area 4sin72°. If a fundamental-region-parallelogram (or any other parallelogram) has a 72° angle, and if its edges have lengths a + bt and c + dt, where a, b, c, d are integers, then its area is (a + bt)(c + dt) sin72° = [(ac + bd) + (ad + bc + bd)t] sin72°, since t2 = t + 1. If this parallelogram is made up of q decagons, 2q pentagons, and r rhombi, its area is [4r + 4qt]sin72°, so

(ac + bd) + (ad + bc + bd)t = 4r + 4qt.
Hence ac + bd = 4r and ad + bc + bd = 4q since t is irrational, so the parallelogram contains (ac + bd)/4 8-gons and (ad + bc + bd)/4 10-gons.
A corollary of this result applies not just to parallelograms but to any fundamental region: if a fundamental region has area 4(r + qt) sin72°, it must be made up of r rhombi, q decagons and 2q pentagons. We shall make use of the corollary in the next section.

5  Creating new patterns

Figure 8 shows a patch of tiles forming a regular pentagon. Such patches occur for instance in the patterns TRY43 and TRY50. We can produce new patterns by rotating the contents of the pentagons, but this must be done in a logical way if we are to preserve some of the symmetry of the pattern. Thinking of the edges of the tiles as braiding, we see that the boundaries of the pentagons in TRY50 form closed pentagonal loops, but in TRY43 we get just a pentagonal section of a much longer finite loop of braiding.
Figure 8: Large pentagon which can be rotated
Figure 9 shows a ten-pointed star. We can find various patterns in which it occurs, and this patch also can be rotated to form new patterns.
Figure 9: Ten-pointed star which can be rotated
Figure 10 shows a rectangle with a pattern of tiles situated on it asymmetrically. Because of the symmetrical layout of the half- and quarter-tiles along the edges, copies of this rectangle and its mirror image can be fitted together in a vertex-to-vertex manner in all possible ways: the partial tiles will always fit together to form complete tiles. By considering the possible ways in which the edges can match, it is possible to enumerate all the tilings that have this marked rectangle as a fundamental region; see Appendix B.
Figure 10: Rectangle for making different patterns
Other smaller rectangles can be fitted together in fewer ways, and sometimes the rectangles will fit together like bricks in a wall. In how many ways can you use the rectangle of Figure 11 as a fundamental region?
Figure 11: Smaller rectangle for making different patterns
Using a rectangle as a fundamental region is a mathematical challenge, but any other way of using a rectangle or other shape to form a pleasing pattern is acceptable.
Figure 12: Perwinkle centre for a tiling
To incorporate the periwinkle flower of Figure 12 into a periodic pattern with symmetry type p1, we were able to enclose it (using trial and error) in a parallelogram that can be used as a unit cell, as shown in Figure 13. To avoid having partial tiles in the unit cell, it has been modified by bumps and indentations like a piece of a jigsaw puzzle. For the complete pattern see Peri1. In Figure 14, rows of these modified cells alternate with rows of their mirror images, to form a different pattern whose type of symmetry is pg. the completed tiling to illustrated, see Peri2, and in Figure 15 the modified cells have been arranged in a regular manner but with gaps. The gaps have the same area as the 72° parallelogram with side-lengths 2+2t and 2+4t, so if the gaps can be filled by tiles we must have three rhombi, five 10-gons and ten pentagons, according to the formula in Section 4. This information eases the search for ways of filling the gap; there is more than one way of doing it. (One solution is given, see Peri3.) The periwinkle is one of several types of flower whose petals have a slight twist so that the flowers have symmetry type c5 rather than d5.
Figure 13: Unit cell with Periwinkle
Figure 14: Periwinkle pattern of type pg (with breaks to show the constituent patches)
Figure 15: Periwinkle pattern with a gap
The pentagonal patch in Figure 8 is made up of two rhombi, one 10-gon and three pentagons (we do not expect the theorem of Section 2 to apply here - this pentagonal patch cannot be used as a unit cell or a fundamental region). This patch has the same area as nine pentagonal tiles, but it cannot be tiled with nine pentagons. Here is an interesting question: does there exist a patch that can be tiled in two ways with different numbers of pentagons and 10-gons?
Finally, the reader is encouraged to enclose the butterfly of Figure 16 (or any other pleasing motif) in a rectangle or other suitable shape that can be repeated to create a periodic pattern.
Figure 16: Butterfly motif

6  Conclusions

In a previous attempt at an enumeration of a completely different nature, a complete list was obtained [6]. It is clear that this is not possible in the present case. The data presented here show the large variety of patterns that can be obtained.
Unfortunately, this modest study does not reflect to complexity of many of the Islamic patterns, as can be seen by the beautiful book [5]. The importance of this book is that is gives some insight into the methods used to construct the classical Islamic patterns.

References

[1]
B. Grünbaum and G. C. Shephard, Tilings and Patterns, W. H. Freeman & Co., New York, NY, 1987.
[2]
B. A. Wichmann, The World of Patterns, CD-ROM and booklet. World Scientific, 2001. ISBN 981-02-4619-6 http://www.worldscientific.com/books/mathematics/4698.html
[3]
J. Bourgoin, Arabic Geometrical Pattern and Design. Dover Reprint 1973. ISBN 0-486-22924-6.
[4]
J. Rigby. A Turkish interlacing pattern and the golden ratio. Mathematics in School. 34 No 1, January 2005. pp16-24.
[5]
G. Necipoglu, The Topkapi Scroll - Geometry and ornament in Islamic architecture. The Getty Center for the History of Art and the Humanities. 1995. ISBN 0-89236-335-5 http://www.getty.edu/bookstore/titles/topkapi.html.
[6]
Brian Wichmann and John Dawes. A New Class of Tilings with Two Prototiles. Visual Mathematics. Vol 3. No 4. 2001. http://www.mi.sanu.ac.yu/vismath/PUB/TWOPUBS.HTM

A  The number of polygons

The table below indicates the number of distinct tilings in our collection having the specified number of 10-gons and 8-gons in a fundamental region. Note that we have made no attempt to find all such tilings. The tilings themselves are listed in Table 1.
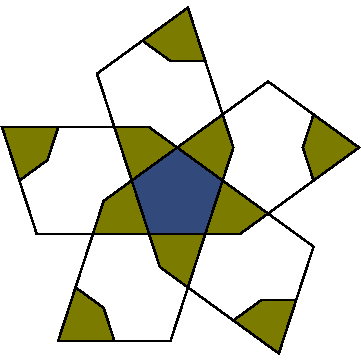
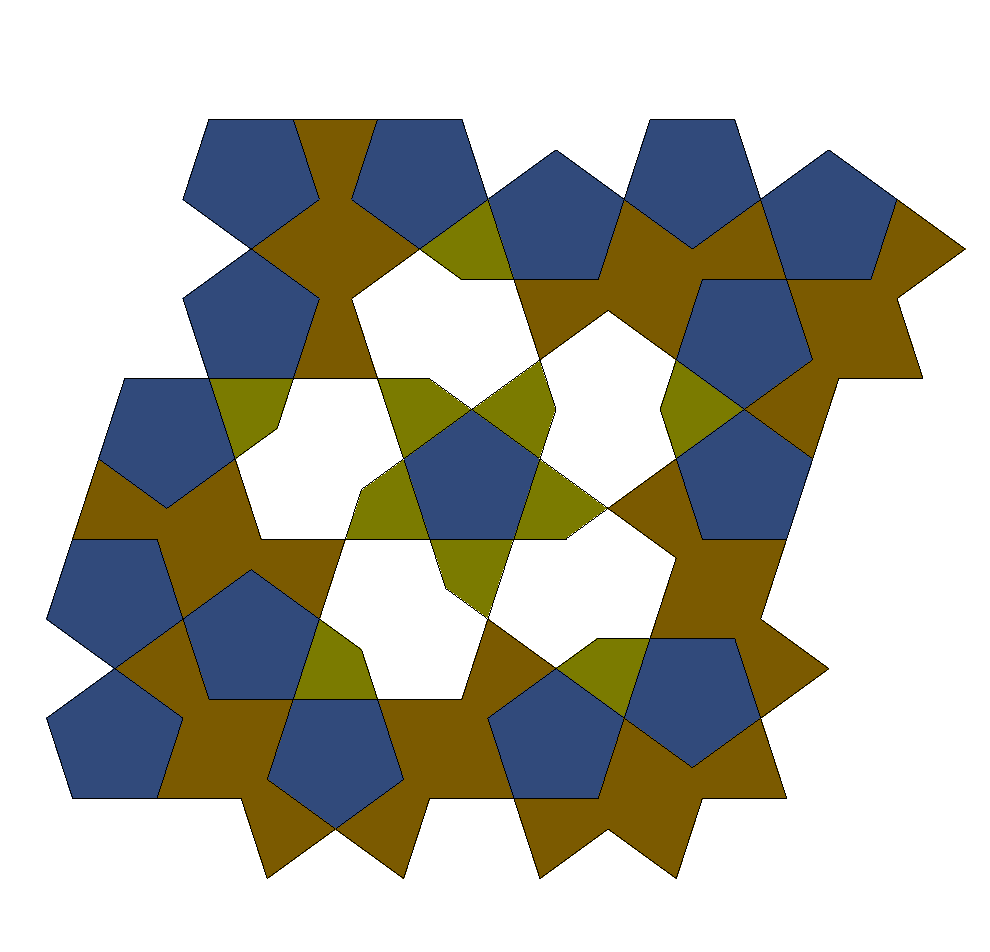
8-gon
10-gon [ 1/4][ 1/2]1 [ 3/2]2 3
[ 1/2]5 4 1 2
[ 3/4]1
1 1 3 3 1
[ 5/4] 1 1
[ 3/2]4 1
2 3
[ 9/4] 1
[ 5/2] 1
3 1
4 24 3
Note that the larger tilings are not included in the above table.

B  Tilings derived from marked rectangles

We consider here the tilings derived from the rectangle in Figure 10. These tilings are necessarily: 2, x | 4, y, AACD - the x is 2 or 3 (when reflections are present) and y is 4 or 5. A total of twenty four such patterns can be created from this one rectangle, encompassing all nine of the plane symmetry types that can be created using our four shapes of tile. The remaining eight plane symmetry types involve 3-fold, 4-fold or 6-fold rotational symmetries; such patterns cannot be created from our four shapes of tile. Any rectangle containing an asymmetrical pattern and with "symmetrical edges" can be used in the same way; this is the simplest one that we have found.
Symmetry G & S class Incidence symbol Name
p1 IH41 [a+b+c+d+;c+d+a+b+] TRY48
pm IH42 [a+b+c+d+;c+b-a+d-] TRY51
pm IH42 [a+b+c+d+;a-d+c-b+] TRY57
pg IH43 [a+b+c+d+;c+d-a+b-] TRY56
pg IH43 [a+b+c+d+;c-d+a-b+] TRY59
cm IH45 [a+b+c+d+;c-b-a-d-] TRY60
cm IH45 [a+b+c+d+;a-d-c-b-] TRY62
p2 IH46 [a+b+c+d+;a+b+c+d+] TRY58
p2 IH47 [a+b+c+d+;c+b+a+d+] TRY49
p2 IH47 [a+b+c+d+;a+d+c+b+] TRY61
pmm IH48 [a+b+c+d+;a-b-c-d-] TRY50
pmg IH49 [a+b+c+d+;a-b+c-d+] TRY63
pmg IH49 [a+b+c+d+;a+b-c+d-] TRY72
pmg IH50 [a+b+c+d+;c+b-a+d+] TRY65
pmg IH50 [a+b+c+d+;c+b+a+d-] TRY73
pmg IH50 [a+b+c+d+;a-d+c+b+] TRY74
pmg IH50 [a+b+c+d+;a+d+c-b+] TRY75
pgg IH51 [a+b+c+d+;c-b+a-d+] TRY48
pm IH42 [a+b+c+d+;c+b-a+d-] TRY51
pm IH42 [a+b+c+d+;a-d+c-b+] TRY57
pg IH43 [a+b+c+d+;c+d-a+b-] TRY56
pg IH43 [a+b+c+d+;c-d+a-b+] TRY59
cm IH45 [a+b+c+d+;c-b-a-d-] TRY60
cm IH45 [a+b+c+d+;a-d-c-b-] TRY62
p2 IH46 [a+b+c+d+;a+b+c+d+] TRY58
p2 IH47 [a+b+c+d+;c+b+a+d+] TRY49
p2 IH47 [a+b+c+d+;a+d+c+b+] TRY61
pmm IH48 [a+b+c+d+;a-b-c-d-] TRY50
pmg IH49 [a+b+c+d+;a-b+c-d+] TRY63
pmg IH49 [a+b+c+d+;a+b-c+d-] TRY72
pmg IH50 [a+b+c+d+;c+b-a+d+] TRY65
pmg IH50 [a+b+c+d+;c+b+a+d-] TRY73
pmg IH50 [a+b+c+d+;a-d+c+b+] TRY74
pmg IH50 [a+b+c+d+;a+d+c-b+] TRY75
pgg IH51 [a+b+c+d+;c-b+a-d+] TRY67
pgg IH51 [a+b+c+d+;a+d-c+b-] TRY76
pgg IH52 [a+b+c+d+;c-d-a-b-] TRY64
cmm IH54 [a+b+c+d+;a-b-c-d+] TRY68
cmm IH54 [a+b+c+d+;a+b-c-d-] TRY69
cmm IH54 [a+b+c+d+;a-b+c-d-] TRY70
cmm IH54 [a+b+c+d+;a-b-c+d-] TRY71
Table 2: List of tilings derived from Figure 10
The Table 2 tabulates all the tilings derived from Figure 10. The underlying analysis follows that of Grünbaum and Shephard [1], Table 6.2.1. Edge a is the bottom edge of Figure 10, and b is the right-hand edge. Note that edge a can only be incident with a or c.


File translated from TEX by TTH, version 3.38.
On 26 Jan 2006, 16:38.

Graphics converted by GraphicConverter.