Enumeration of 2-isohedraltilings on the sphereElizaveta Zamorzaeva
Faculty of Mathematics and Informatics |
Abstract: The enumeration of 2-isohedral tilings of a 2-dimensional sphere with disks is given. Fundamental Delone classes of 2-isohedral tilings are presented in a table of pictures. |
Consider a 2-dimensional sphere, which is one of three 2-dimensional spaces of constant curvature. Let each tile of a tiling W of the sphere be the closure of an open connected and simply connected domain. Let G be a discrete isometry group of the sphere (a point group). The tiling W is k-isohedral with respect to the group G if G maps W onto itself and all the tiles of W form exactly k transitivity classes under the group G. Two pairs (W,G) and (W',G') are of the same Delone class if there exists a homeomorphism f of the sphere with f(W) = W' and G' = fGf-1. The above and some below concepts and definitions hold for all three 2-dimensional spaces of constant curvature (see [1, 2]).
A Delone class (W,G) is called (h1, h2, ..., hk)-transitive if the group G acts hi times transitively on the i-th class of tiles of the tiling W, i = 1, 2, ..., k. If h1 = h2 = ... = hk = 1, the Delone class (W,G) is called fundamental, otherwise non-fundamental. Isohedral tilings of the Euclidean plane were studied by many scientists [3-5]. A survey of results on tilings of the plane with transitivity properties is given in [6]. The complete classification of isohedral (as well as isogonal and isotoxal) tilings of the sphere and references are given in [7]. General methods for finding k-isohedral (k ³ 2) tilings of the 2-dimensional space of constant curvature (i.e. the Euclidean plane, the sphere or the hyperbolic plane) using the known isohedral tilings were developed by the author in [1]. Applying these methods the author obtained the complete classification of 2-isohedral tilings of the sphere shown in tables of pictures. With the help of Delaney-Dress symbols, the same methods were implemented [8] in algorithms and computer programmes. The Delaney-Dress symbols corresponding to 2-isohedral tilings of the sphere were obtained, the numerical results are given in [8]. Then a computer programme was elaborated that, given a Delaney-Dress symbol, produces a picture of the corresponding tiling of the sphere (or of the Euclidean plane or hyperbolic plane). The table of 2-isohedral tilings of the sphere was published in [9]. Considering that the paper [9] is hardly available (and written in Russian) and taking in account the broad applied significance of the results (in particular, for designers) we have made decision to publish in electronic form the enumeration of 2-isohedral tilings of the sphere. The complete classification of 2-isohedral tilings of the Euclidean plane was obtained earlier both by the author and German mathematicians. The results shown in a table of pictures were published in a joint paper [2].
Now introduce the elements of a tiling. In [1, 2] some concepts were defined and justified for the Euclidean plane, but for the 2-dimensional sphere similar statements are valid. Most often we need not give the proofs supplementing [1, 2], because a tiling of the sphere may contain only finitely many tiles, the fact simplifying the consideration. In a tiling of the sphere a connected component of the intersection of two or more different tiles is called a vertex of the tiling if it is a single point, otherwise it is called an edge of the tiling. Tiles, edges and vertices are called elements of a tiling.
Turn to discrete isometry groups of a 2-dimensional sphere. These groups may be considered as 3-dimensional isometry groups with an invariant point - the centre of the sphere - and are well known. The enumeration of these groups is given in [7], but in this paper we prefer to use for them other symbols - orbifold symbols [10] - which reflect their nature as isometry groups of a sphere. Such symbolism is common for all three 2-dimensional spaces of constant curvature. The explanation of the Conway's orbifold symbol, which is equivalent to the Macbeath's group signature, can be found in [11].
Describe briefly the idea of orbifold symbols. Let X be one of the three 2-dimensional spaces of constant curvature and G be an isometry group of X with a compact fundamental domain. Consider the quotient M = X/G, which is a compact 2-dimensional manifold, possibly with boundary. Any point x ÎX with the non-trivial stabilizer group Gx = {gÎG | g(x) = x} gives rise to a cone point (x-, v) of degree v if Gx is a rotation group of order v, or to a corner point of degree v if Gx is a dihedral group generated by a v-fold rotation and a reflection. Here x- denotes the equivalence class of points containing x. The orbifold symbol can be obtained by specifying the following four items:
(O1) The number of handles h if M is orientable, or the number of cross-caps k otherwise.
(O2) The system of branching numbers v for all cone points.
(O3) The number of boundary components q.
(O4) For each boundary component B one must list the branching numbers of all corner points lying on B in a cyclic order. If M is orientable one must list the corner points of each boundary component in the order induced by a fixed orientation of the underlying manifold.
The rules for writing down the orbifold symbol are the following: First, if M is orientable with h handles one writes h small circles: ° ° ° ... Second, the branching numbers for all cone points are listed. Next, each boundary component is indicated by a star: *, followed by the list of branching numbers encountered while going around the boundary component. Finally, if M is not orientable with k cross-caps one writes k crosses: ×××...
There are 4 countable series of the isometry groups of the sphere given by the following orbifold symbols: nn, n×, n*, *nn, 22n, 2*n, *22n where n = 1, 2, .... Also there are 7 separate isometry groups of the sphere with the following orbifold symbols: 322, 3*2, *332, 432, *432, 532, *532. The complete classification (enumeration) of the isohedral tilings on a sphere is given in [7].
The method of finding k-isohedral (k ³2) tilings is based on the following theorem.
Theorem. Let a tiling W of the 2-dimensional sphere with disks be k-isohedral (k ³ 2) with respect to an isometry group G, the Delone class (W,G) being fundamental. Then one can glue pairwise the disks of some two classes of the tiling W along the edges equivalent under the group G so that the resulted tiling W' of the sphere with disks is (k-1)-isohedral with respect to the group G, the Delone class being fundamental. If W is a tiling of the sphere with only two disks, the gluing yields the whole sphere.
The theorem is proved in [1, 2] for the case of the Euclidean plane, but in the case of the sphere the proof only simplifies.
Given a k-isohedral (k ³2) tiling W of the sphere with disks, the Delone class (W,G) being fundamental, the application of gluing operation 1, 2, ..., k-2, k-1 times yields, respectively, (k-1)-isohedral, (k-2)-isohedral, ..., 2-isohedral and, finally, isohedral with respect to the group G fundamental tiling of the sphere with disks. Vice versa, given a (k-1)-isohedral tiling with the fundamental Delone class (W',G), one can obtain a k-isohedral tiling with the fundamental Delone class (W,G) using the following procedure: divide one disk of the tiling by means of a simple curve into two disks and apply to this curve the group G. In [2] this procedure is called SPLIT. Due to the above theorem to obtain all possible Delone classes of k-isohedral (k ³ 2) tilings of the sphere with disks for a given group G one must apply the procedure SPLIT to all the fundamental Delone classes of (k-1)-isohedral tilings of the sphere with this group G by all possible ways yielding different Delone classes [1]. Thus, known the fundamental Delone classes of isohedral tilings of the sphere for some group G, one can obtain all the fundamental k-isohedral tilings of the sphere with disks for the same group G, where k is a fixed integer, k ³ 2.
Remark that known all the fundamental Delone clases of k-isohedral tilings of the sphere for some group G, one can obtain all the non-fundamental Delone classes of k-isohedral tilings of the sphere for the same group G using the procedure GLUE described in [1, 2].
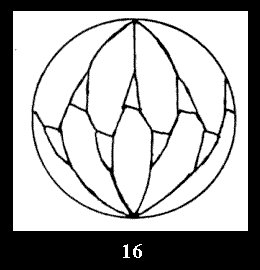
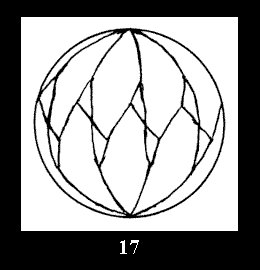
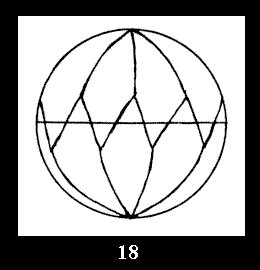
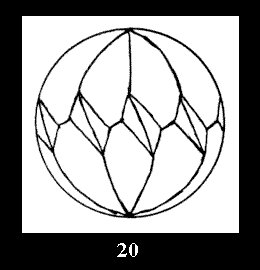
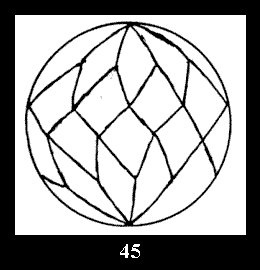
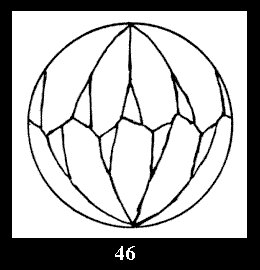
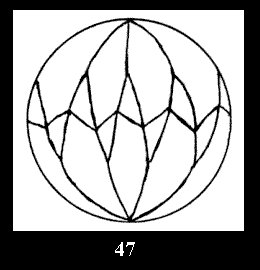
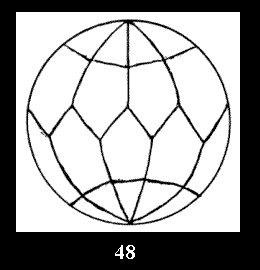
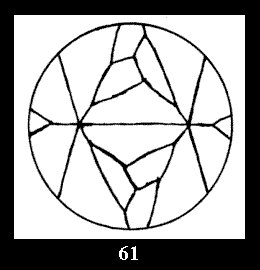
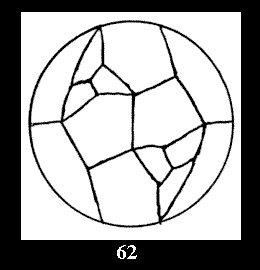
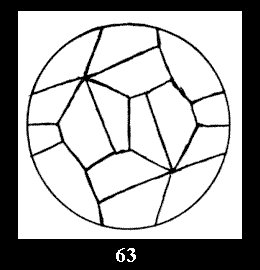
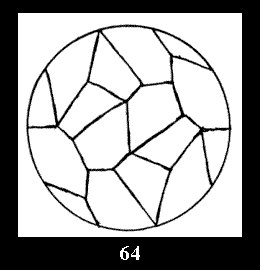
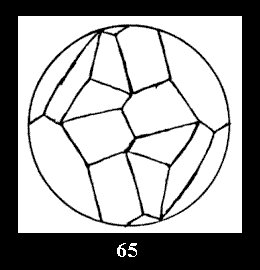
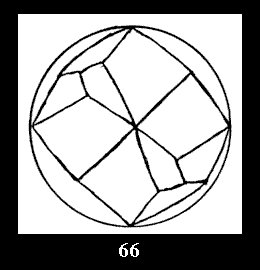
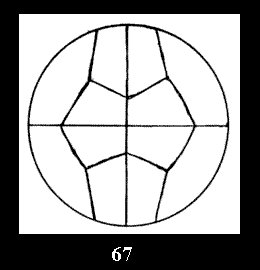
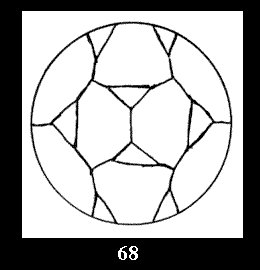
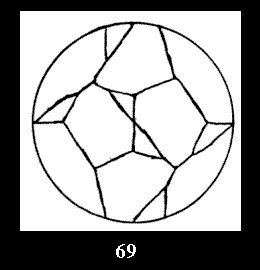
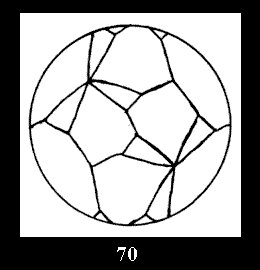
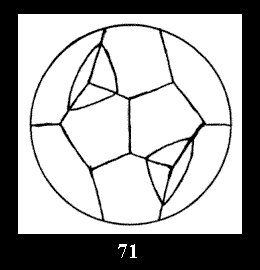
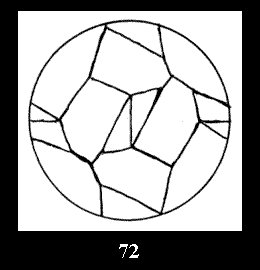
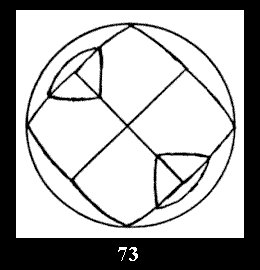
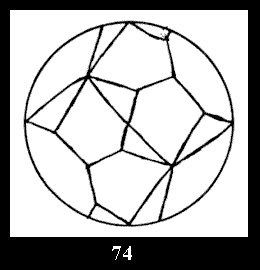
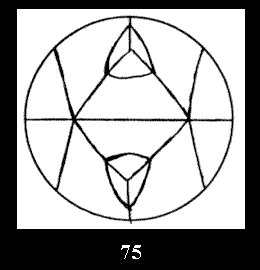
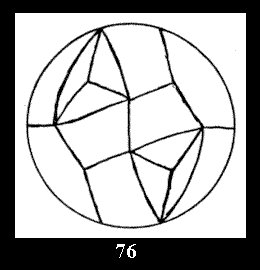
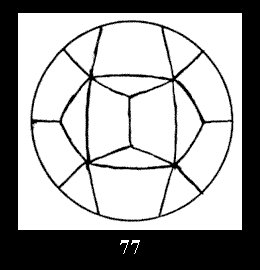
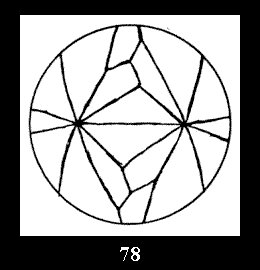
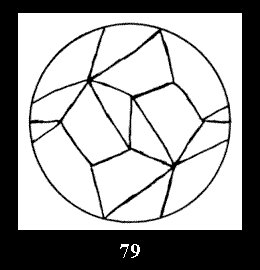
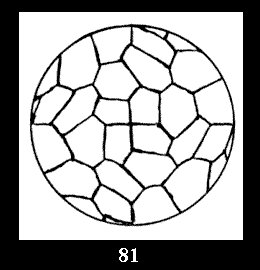
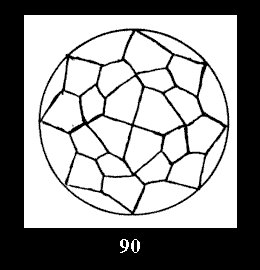
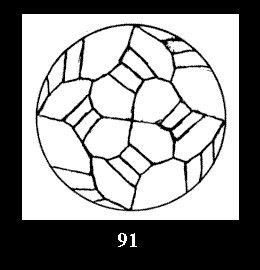
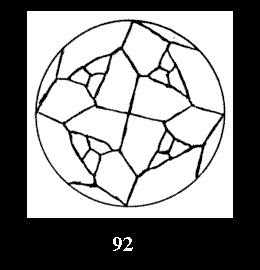
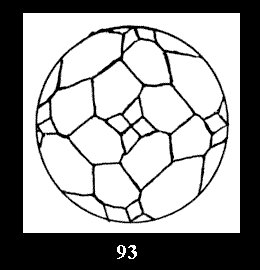
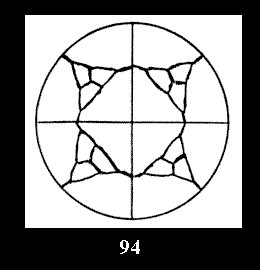
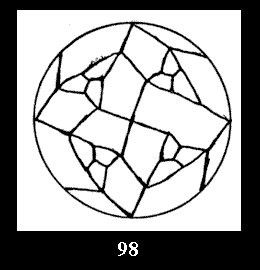
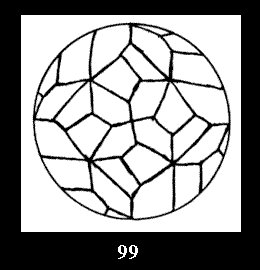
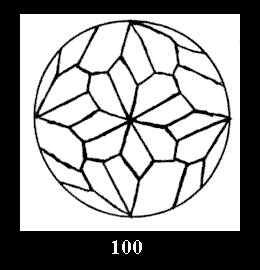
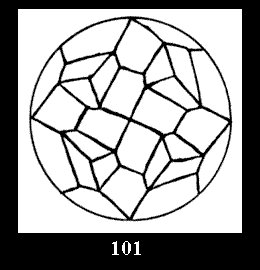
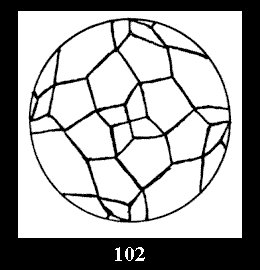
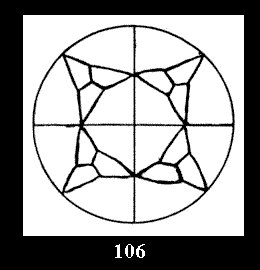
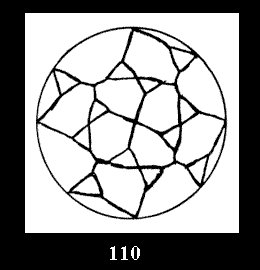
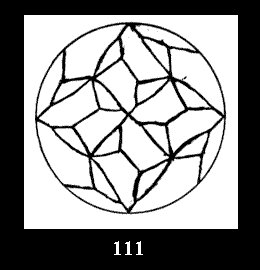
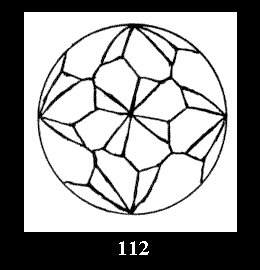
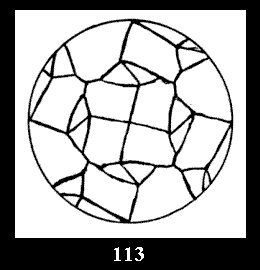
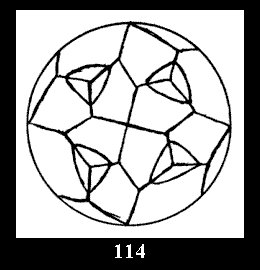
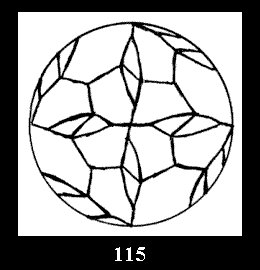
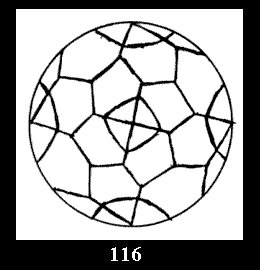
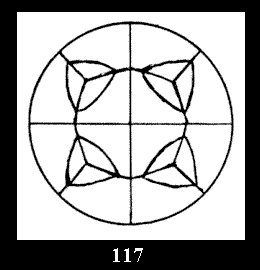
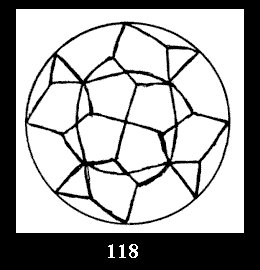
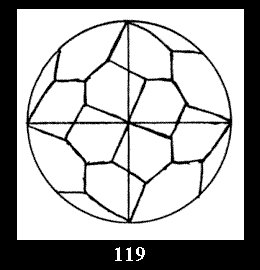
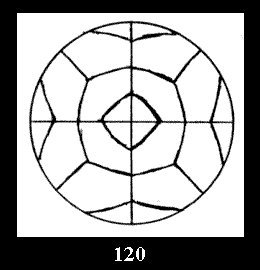
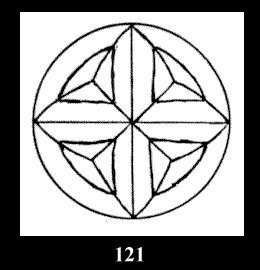
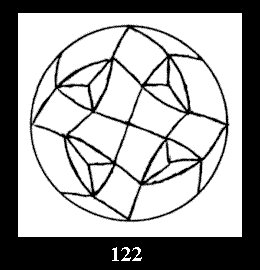
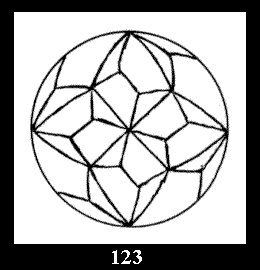
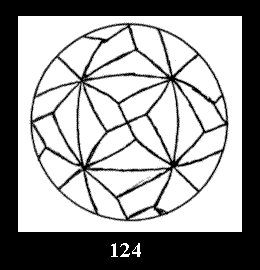
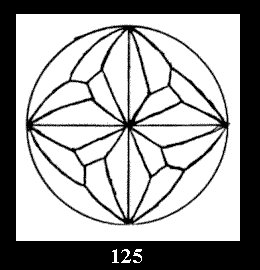
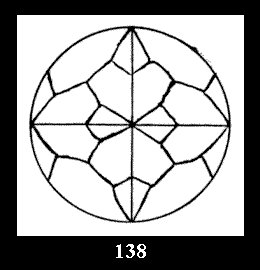
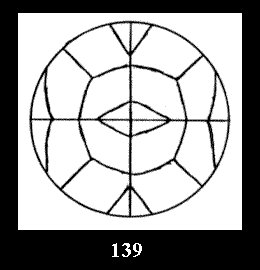
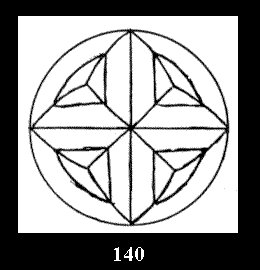
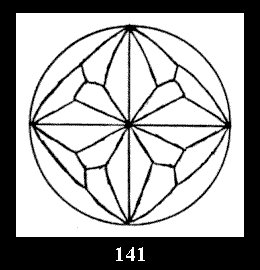
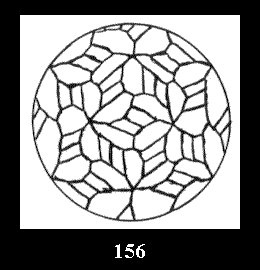
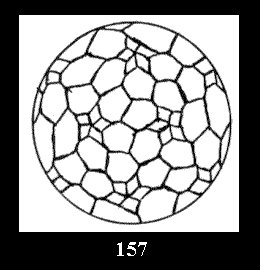
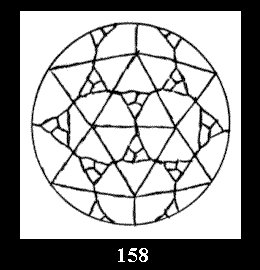
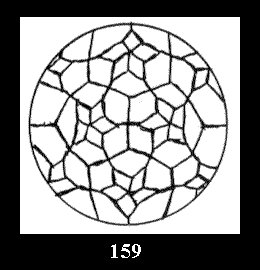
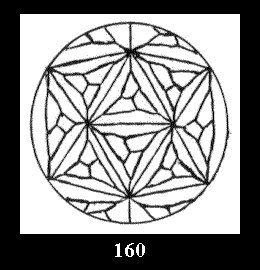
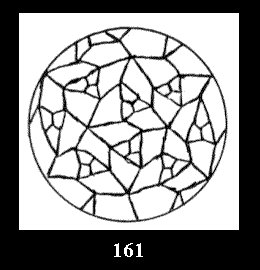
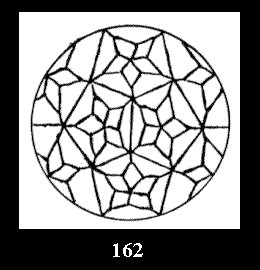
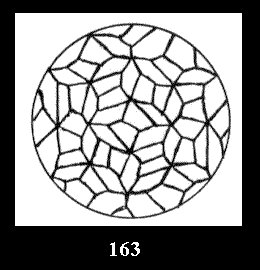
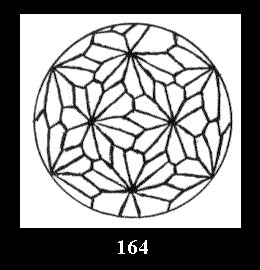
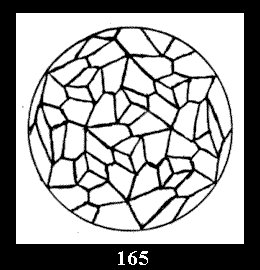
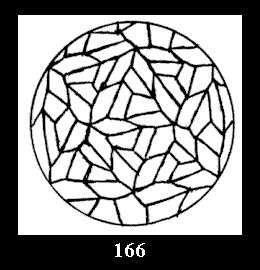
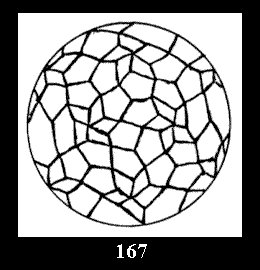
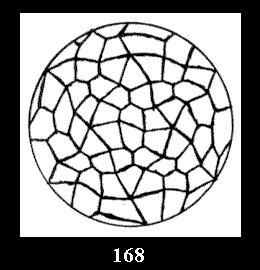
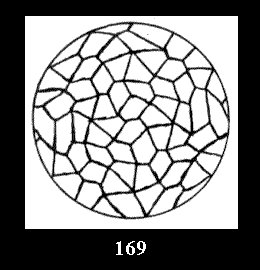
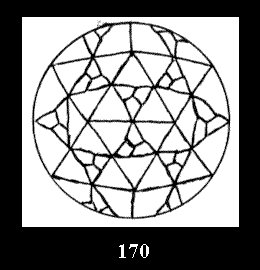
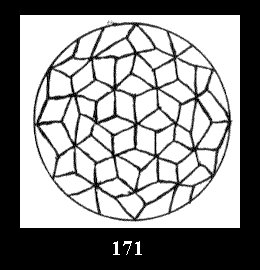
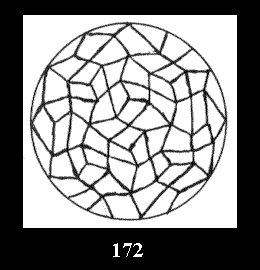
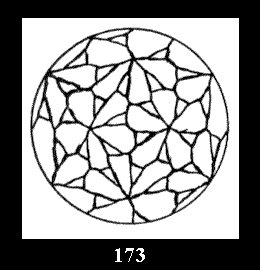
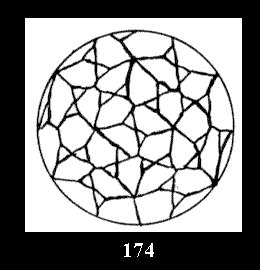
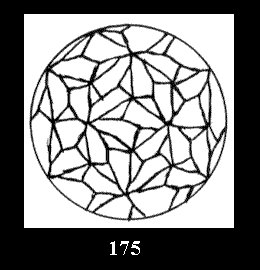
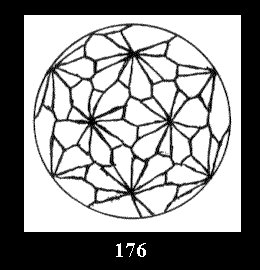
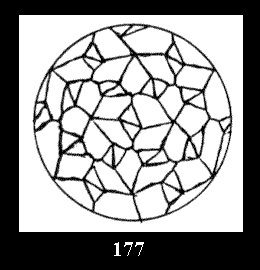
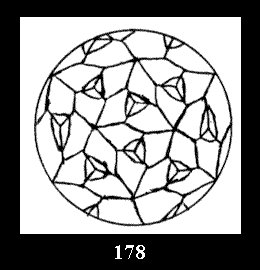
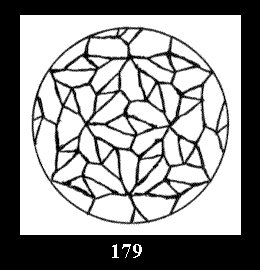
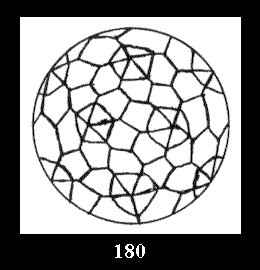
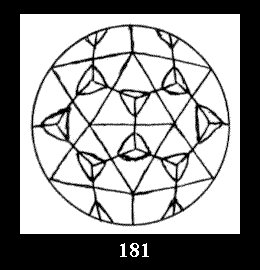
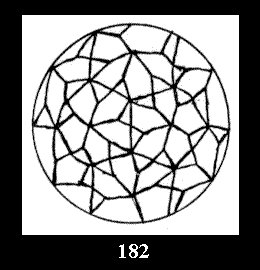
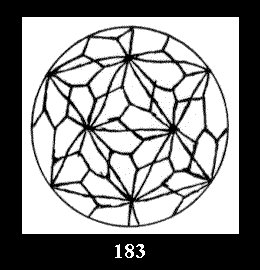
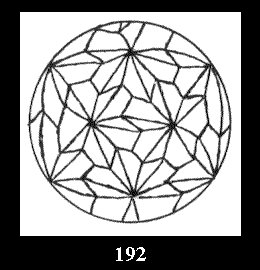
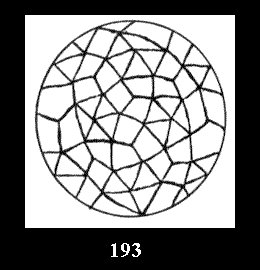
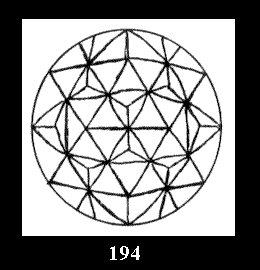
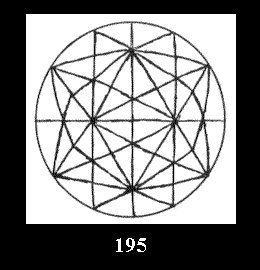
Applying the procedure SPLIT 'by hand' the author obtained all the possible Delone classes of 2-isohedral tilings of the sphere with disks in tables of pictures. Because of the large number of the resulted Delone classes we restrict ourselves with fundamental Delone classes and give pictures only for normal in terminology [6] tilings, for non-normal tilings we give only numerical data.
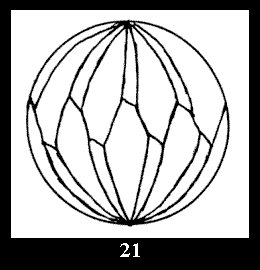
For the series of groups *nn there is 1 series
of the fundamental Delone classes of normal 2-isohedral tilings of the
sphere with disks (Fig. 1) and 3 series of tilings with
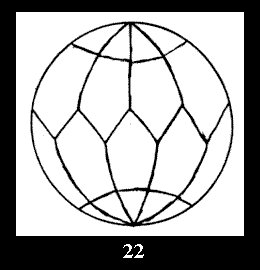
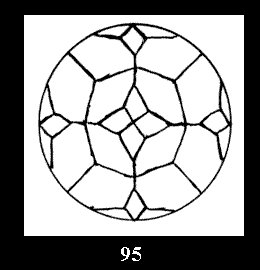
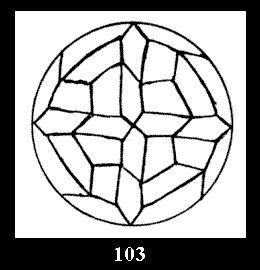
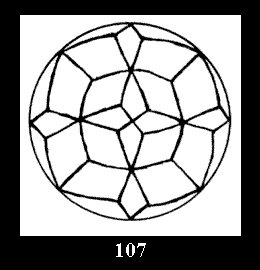
diagonal disks (altogether 4 series). For the series of groups nn
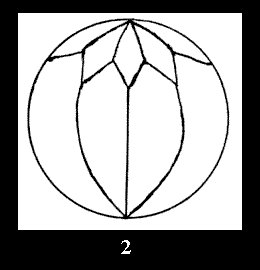
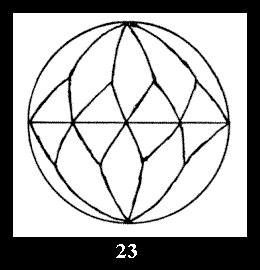
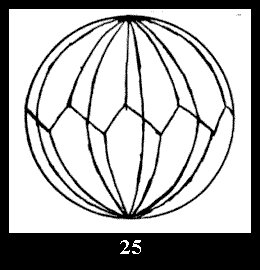
there are 2 series of normal tilings (Fig. 2, 3) and
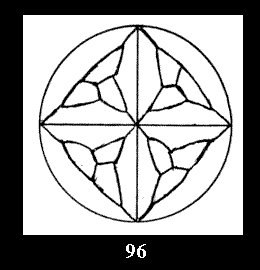
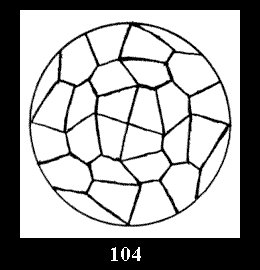
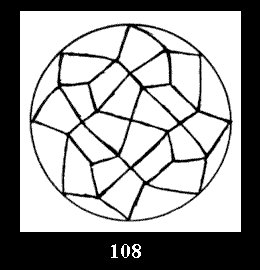
3 series of tilings with digons (altogether 5 series). For the series *22n
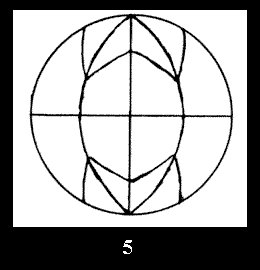
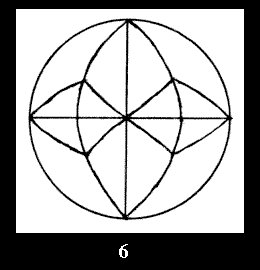
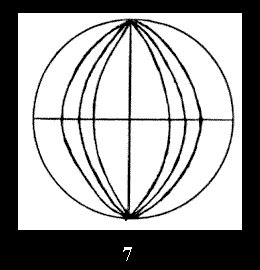
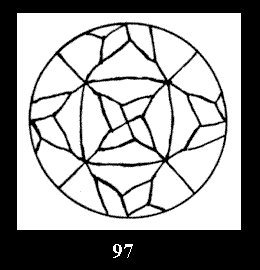
there are, respectively, 4 series (Fig. 4-7) and 7 series
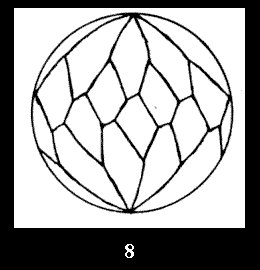
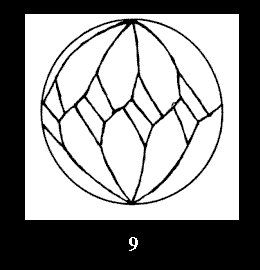
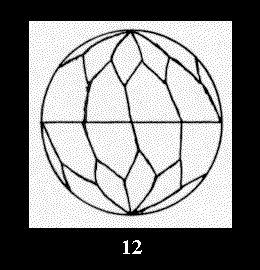
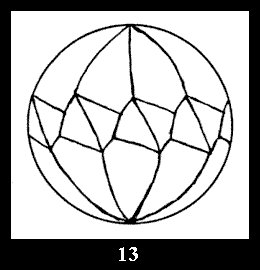
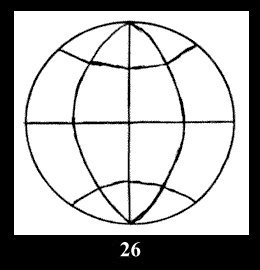
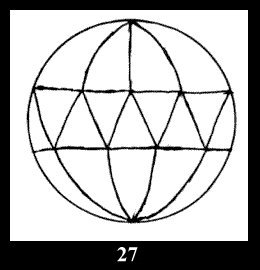
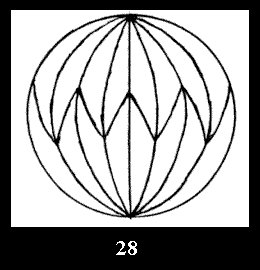
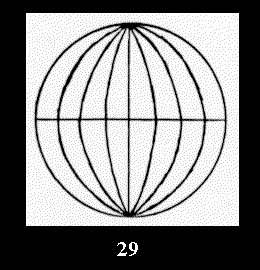
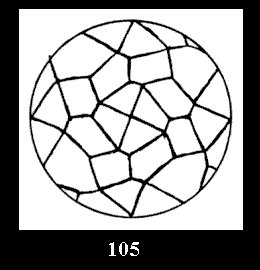
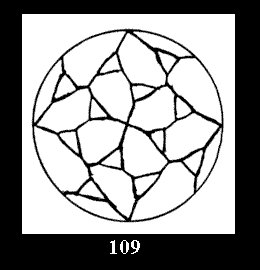
(altogether 11). For 22n there are 22 series of normal tilings (Fig.
8-29), 6 series of non-normal tilings without digonal
disks and 26 series of tilings with digons (altogether 54). For n*
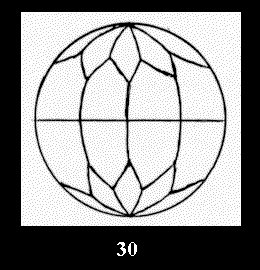
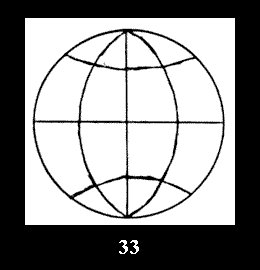
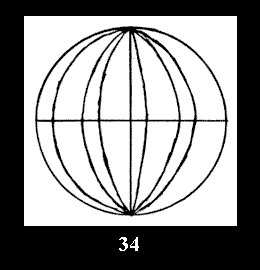
there are, respectively, 5 series (Fig. 30-34), 0 and
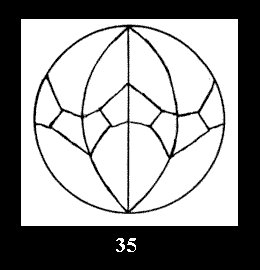
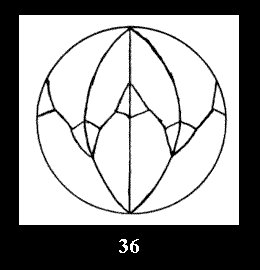
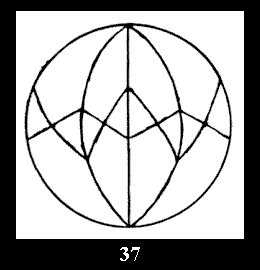
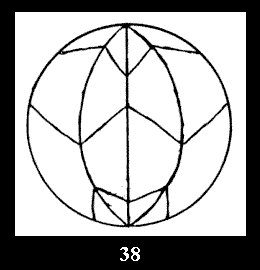
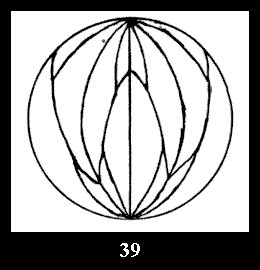
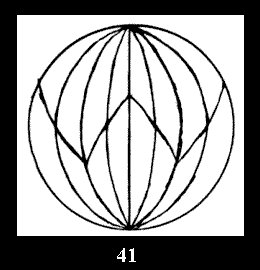
7 series (altogether 12). For 2*n there are, respectively, 7 series
(Fig. 35-41), 4 series and 18 series (altogether 29).
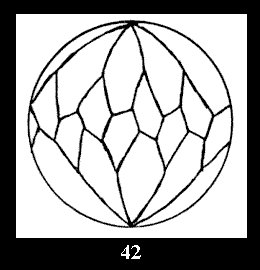
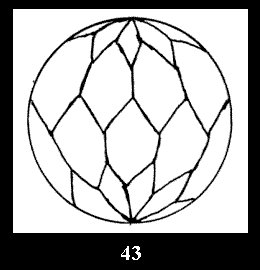
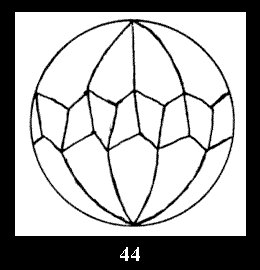
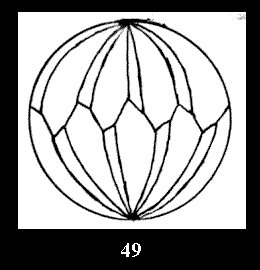
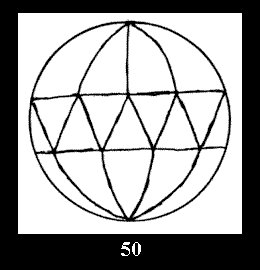
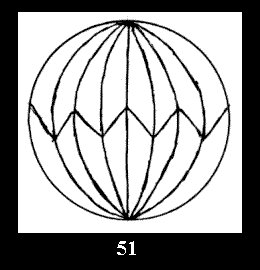
For n× there are, respectively, 10 series (Fig.42-51),
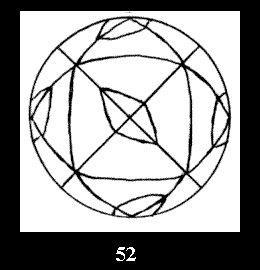
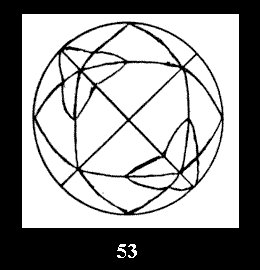
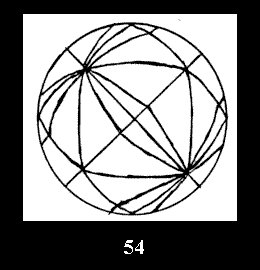
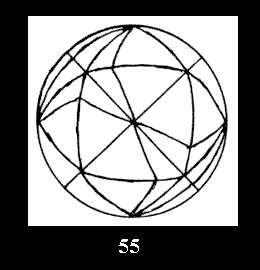
0 and 10 series (altogether 20). For the group *332 there are 4 fundamental
Delone classes of normal 2-isohedral tilings of the sphere with disks (Fig.
52-55) and 7 Delone classes of tilings with digonal
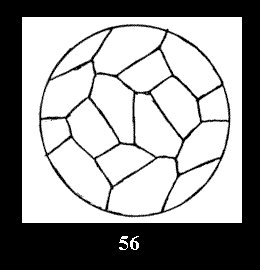
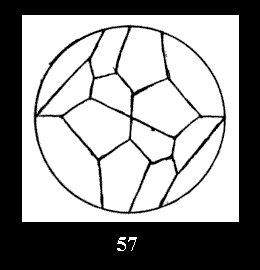
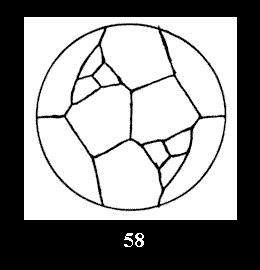
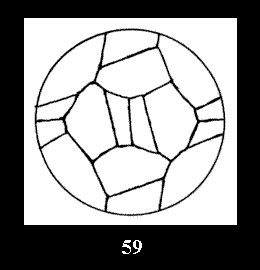
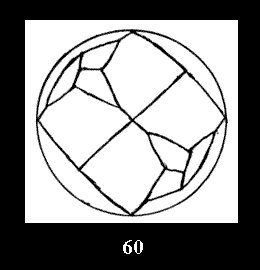
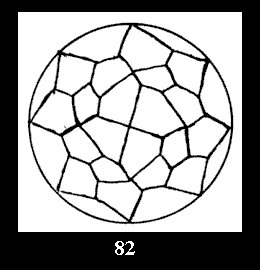
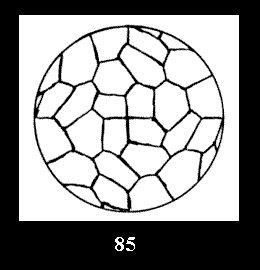
disks (altogether 11). For the group 332 there are 26 Delone classes of
normal tilings (Fig. 56-81), 4 Delone classes of non-normal
tilings without digonal disks and 24 Delone classes of tilings with digons
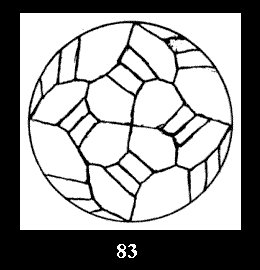
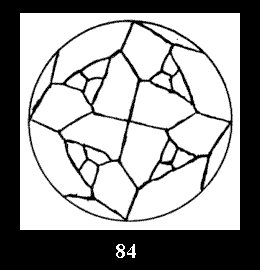
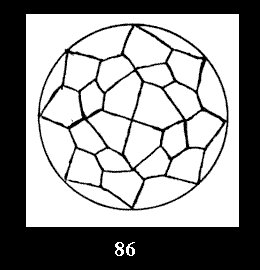
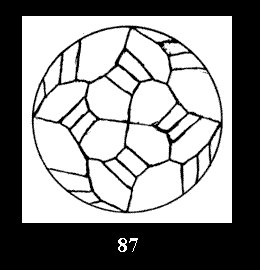
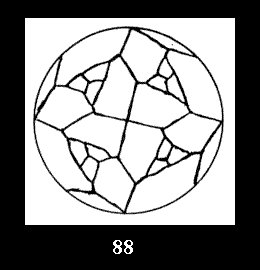
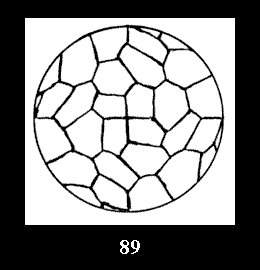
(altogether 54). For *432 there are 6 normal tilings (Fig. 82-87),
0 non-normal tilings without digons and 12 tilings with digons (altogether
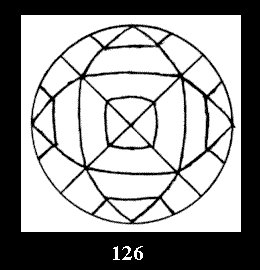
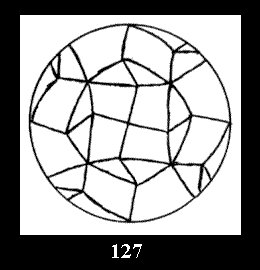
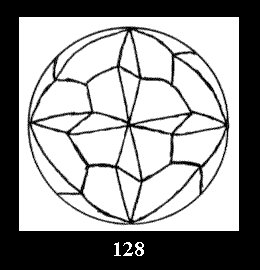
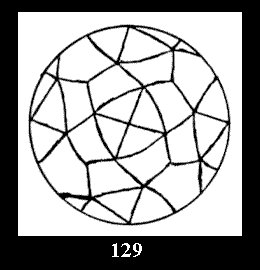
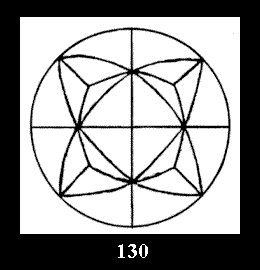
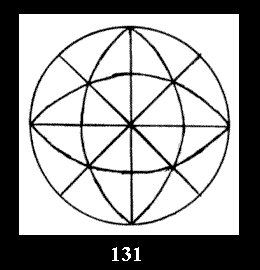
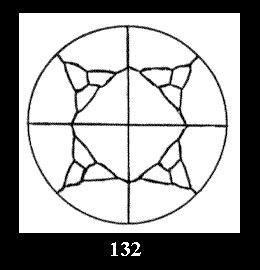
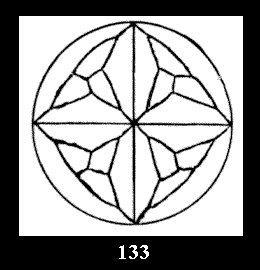
18). For 432 there are, respectively, 44 tilings (Fig. 88-131),
6 and 42 tilings (altogether 92). For 3*2 there are, respectively, 14 tilings
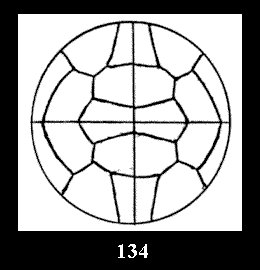
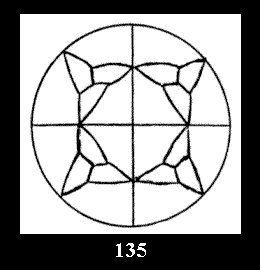
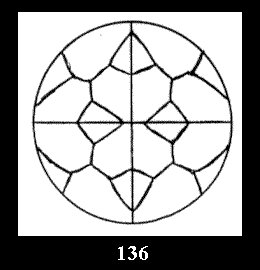
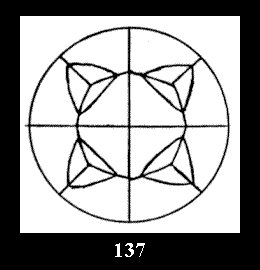
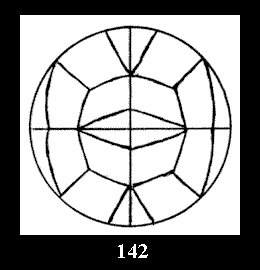
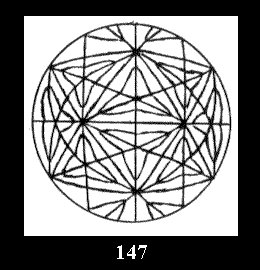
(Fig. 132-145), 0 and 15 tilings (altogether 29). For
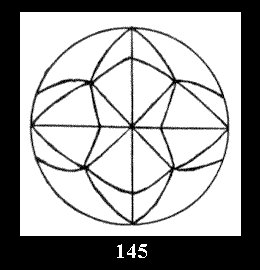
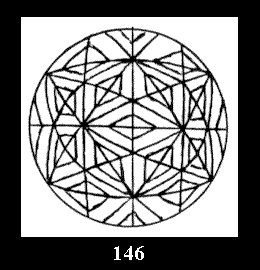
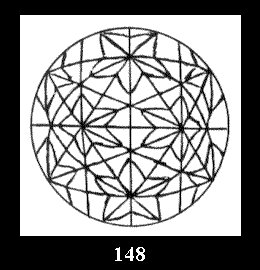
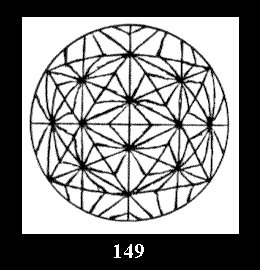
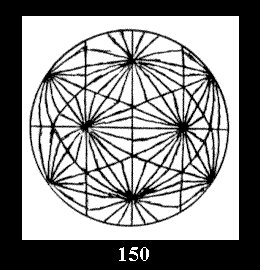
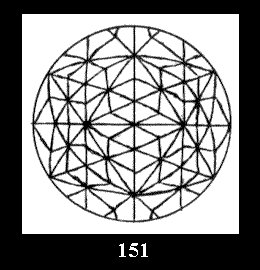
*532 there are, respectively, 6 tilings (Fig. 146-151),
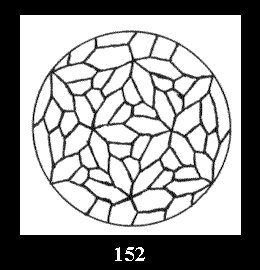
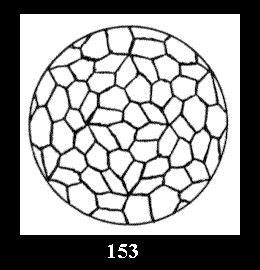
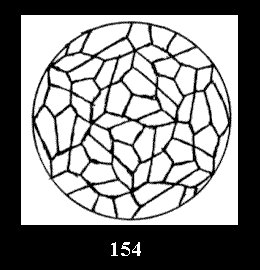
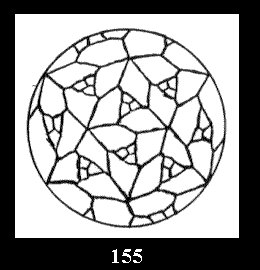
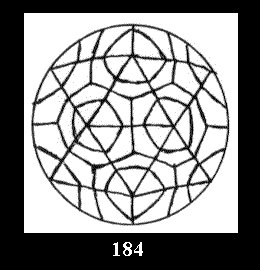
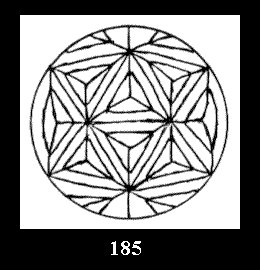
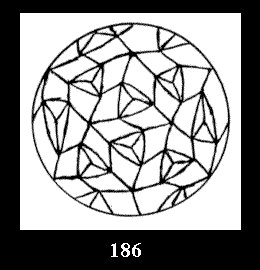
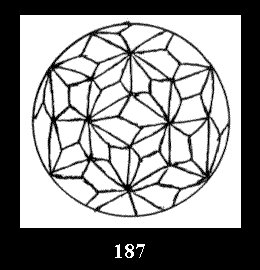
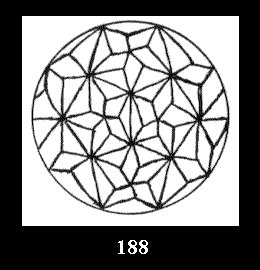
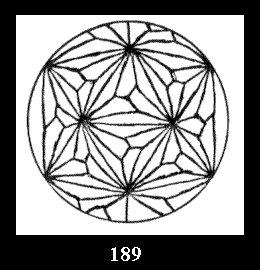
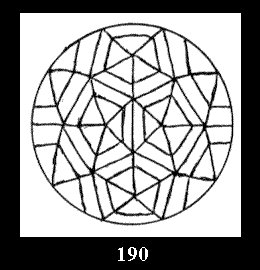
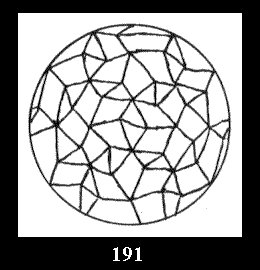
0 and 12 tilings (altogether 18). For 532 there are, respectively, 44 tilings
(Fig. 152-195), 6 and 42 tilings (altogether 92). Remark
that for small orders of rotation (1 and 2) the number of tilings corresponding
to the given group may be less than in the series. For each series one
tiling is drawn (for r = 4 or r = 8). Numerical data of the
obtained Delone classes of isohedral tilings of the sphere with disks for
all series and isometry groups coincide with numerical data of work [8].
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
References
- [1] Zamorzaeva E. A., On sorts of two-dimensional multiregular tilings, Izv. Akad. Nauk Respub. Moldova. Mat. (1992), no. 1, 59-66 (in Russian).
- [2]
- Delgado O., Huson D. and Zamorzaeva E., The classification of 2-isohedral tilings of the plane, Geom. Dedicata 43 (1992), 43-117.
- [3]
- Delone B. N., Theory of planigons, Izv. Akad. Nauk SSSR. Ser. Mat. 23 (1959), 365-386 (in Russian).
- [4]
- Delone B. N., Dolbilin N. P. and Shtogrin M. I., Combinatorial and metrical theory of planigons, Tr. Mat. Inst. Steklov Akad. Nauk SSSR 148 (1978), 109-140 (in Russian); English translation: Proc. Steklov Inst. Math. 4 (1980), 111-141.
- [5]
- Heesch H. Reguläres Parkettierungsproblem, Westdeutscher Verlag, Cologne, 1968.
- [6]
- Grünbaum B. and Shephard G. C., Tilings and Patterns, Freeman, New York, 1987.
- [7]
- Grünbaum B. and Shephard G. C., Spherical tilings with transitivity properties, The Geometric Vein. The Coxeter Festschrift, Springer-Verlag, 1982, 65-98.
- [8]
- Huson D. H., The generation and classification of tile-k-transitive tilings of the Euclidean plane, the sphere and the hyperbolic plane, Geom. Dedicata 47 (1993), 269-296.
- [9]
- Zamorzaeva E. A., Classification of 2-isohedral tilings of the sphere, Izv. Akad. Nauk Respub. Moldova. Mat. (1997), no. 3, 74-85 (in Russian).
- [10]
- Conway J. H., The orbifold notation for surface groups, Groups, Combinatorics and Geometry, London Math. Soc. Lecture Note Series 165, Cambridge University Press, 1992, 438-447.
- [11] Balke L. and Huson D. H., Two-dimensional groups, orbifolds and tilings, Geom. Dedicata 60 (1996), 89-106.