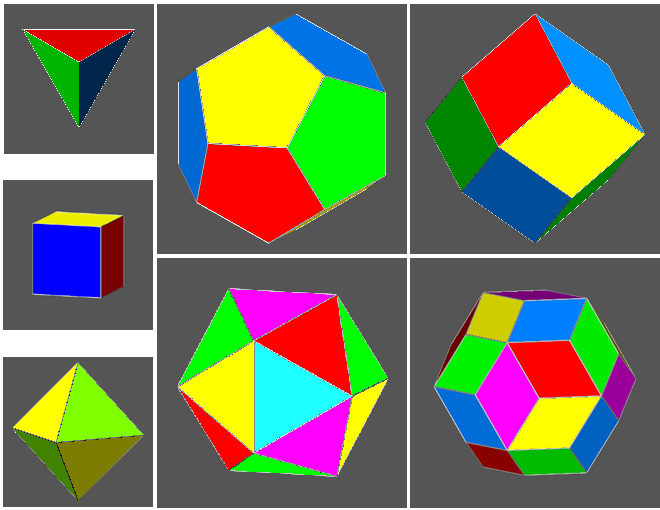
The most obvious colouring procedure assigns different colours to faces sharing an edge; a more restrictive condition can also prevent the sharing of vertices by equally coloured faces.
The previous criteria are essentially aesthetical; conversely, if face
colouring is used to represent some features of the current crystallographic symmetry of
a polyhedron, its colouring will be different and sharing of edges
may occur between faces having an equal colour and belonging to the same simple form.
In the sequel, colouring of the five convex regular (or Platonic) polyhedra and of two
interesting Catalan polyhedra, the rhombic dodecahedron and rhombic triacontahedron, will be discussed.
Note: when the mouse hovers on underlined words or some images,
the symbol of a pointer appears: if the web browser is set up to visualize VRML (Virtual Reality Modeling
Language) files, by clicking with the left button of the mouse it should be possible
to visualize in a new window a dynamic image, with which one can interact by rotating it, shifting it, changing its dimensions...
A good Web3D visualizer can be found at the following address:
http://www.parallelgraphics.com/products/cortona/
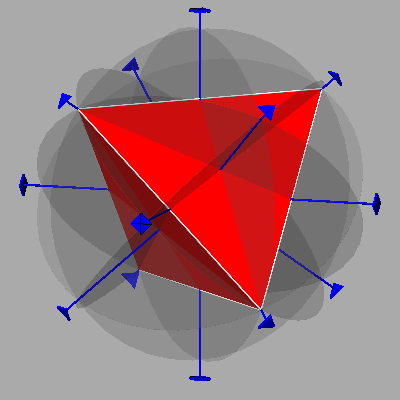
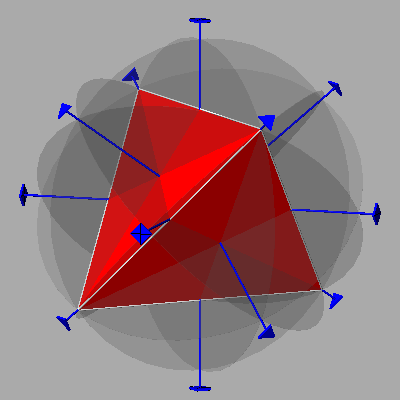
The
tetrahedron, consisting of four equilateral triangular faces,
six edges and four vertices, is the only regular polyhedron
with an equal number of faces and vertices: consequently, it is also the only autodual polyhedron
(remember that duality implies the exchange of faces and vertices between two polyhedra,
concerning both their number and their position).
 |
 |
|
The images of these tetrahedra and most of the
followings have been obtained by Shape 7.0, a program for drawing the morphology of crystals provided by Shape Software. |
The symmetry elements characterizing the tetrahedron are:
- four 3-fold rotation axes, each one perpendicular to a face and passing through the opposite vertex
- three 4-fold rotoinversion axes, each one passing through the middle points of a pair of opposite edges
- six mirror planes, each one passing through both the edge shared by two faces and the middle point of the opposite edge shared by the other two faces split into 2 equal parts by the plane itself.
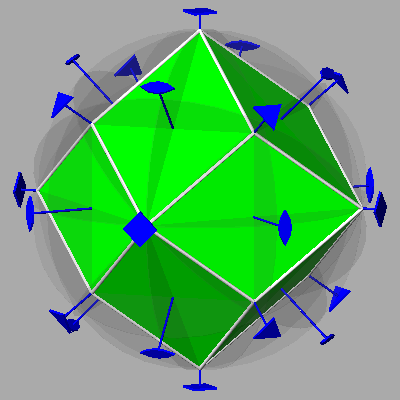
The cube, characterized by 6 square faces, 8
vertices and 12 edges, is the dual of the
octahedron, in turn characterized by 8 triangular equilateral faces, 6
vertices and 12 edges (according to the well-known rule stating that in every
polyhedron the sum of the number of faces and vertices corresponds to the number
of edges increased by two).
|
|
|
- three 4-fold rotation axes, each one perpendicular to a pair of parallel faces of the cube and passing through two opposite vertices of the octahedron
- three mirror planes perpendicular to these 4-fold rotation axes, named principal planes
- four 3-fold rotation axes each one perpendicular to a pair of parallel faces of the octahedron and passing through two opposite vertices of the cube
- six 2-fold axes passing through the middle points of opposite edges in both polyhedra
- three mirror planes perpendicular to these 2-fold rotation axes, named secondary planes
- an inversion centre, as a consequence of the association of even rotation
axes (both 2-fold and
4-fold) with planes placed orthogonally to them
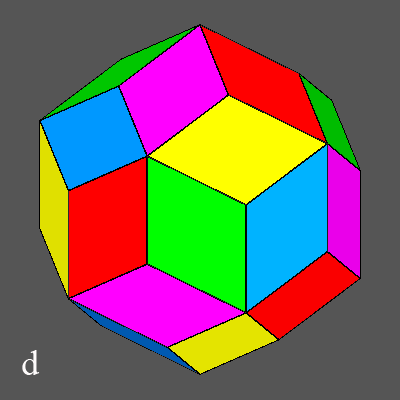
The polyhedron formed by twelve rhombic faces, perpendicular to the directions corresponding to the six two-fold axes previously mentioned, is named rhombic dodecahedron and belongs to the family of Catalan polyhedra, duals of semiregular Archimedean polyhedra. In particular, the rhombic dodecahedron is the dual of the cuboctahedron, a polyhedron with 14 faces (6 square and 8 equilateral triangular ones) given by a particular combination of two forms, a cube and an octahedron. Actually in the cuboctaedron every vertex is shared by two pairs of squares and equilateral triangles as a consequence of a proper ratio between the distances, from the centre of the cuboctahedron, of the faces belonging to cube and octahedron.
 |
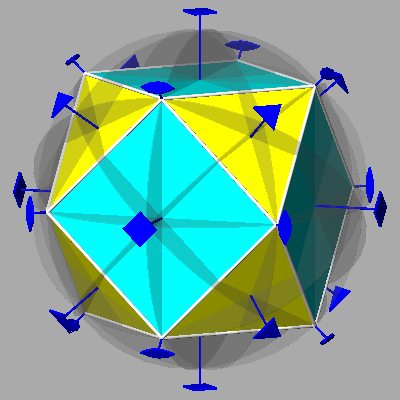 |
Concerning the two remaining regular polyhedra, the icosahedron, characterized by 20 triangular faces, 12 vertices and 30 edges, is the dual of the dodecahedron, in turn characterized by 12 pentagonal faces, 20 vertices and 30 edges.
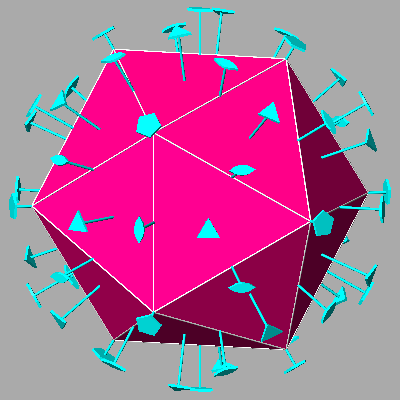 |
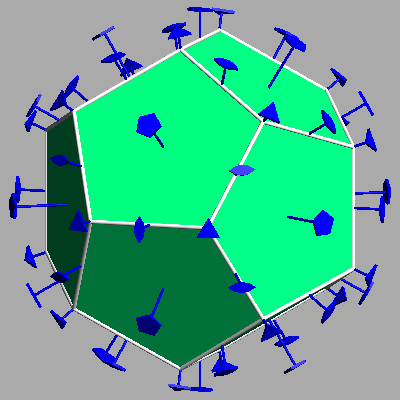 |
- ten 3-fold axes, orthogonal to every couple of parallel faces in the icosahedron and passing through pairs of opposite vertices in the dodecahedron
- six 5-fold axes, orthogonal to every couple of parallel faces in the dodecahedron and passing through pairs of opposite vertices in the icosahedron
- fifteen 2-fold axes (which, together with the fifteen mirror planes orthogonal to them, imply the presence of an inversion centre) passing through the middle points of opposite edges in both polyhedra .
The polyhedron formed by 30 rhombic faces, placed in pairs perpendicular to each
of the fifteen 2-fold axes
present in both the
Incidentally, one can note that, in case of polyhedra made of different forms, where each face does not share any edge with other faces belonging to the same form (as it happens for example with the icosidodecahedron and the cuboctahedron, classified as quasi-regular polyhedra for this reason), in order to highlight the single faces it is sufficient to assign a different colour to each form of the polyhedron.
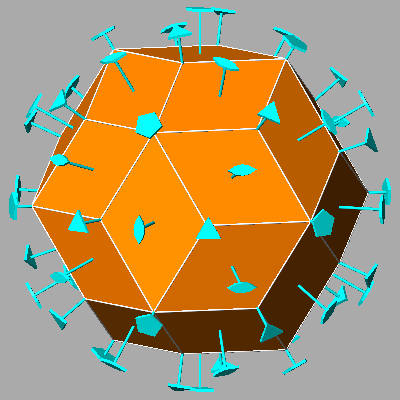 |
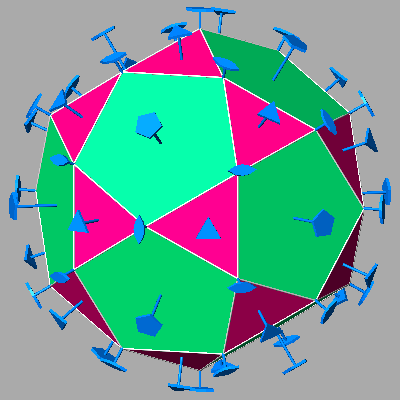 |
Whereas in the rhombic dodecahedron the ratio between
the lengths of the diagonals of each rhombic face is equal to √2, in the rhombic triacontahedron
such ratio is equal to
The following review of the schemes for colouring
different polyhedra, starting from the notions contained in George Hart's page:
http://www.georgehart.com/virtual-polyhedra/colorings.html,
goes into further depth concerning the crystallographic facet of polyhedra colouring.
 |
 |
The maximum crystallographic symmetry of the tetrahedron, which coincides with the geometrical symmetry, corresponds to the 43m point group. On the other hand, any kind of symmetry would be absent if one take into account the different colouring of the faces.
Introducing the n-fold chromatic symmetry operators, represented by a prime mark (n'), which relate equivalent faces ignoring their colours, the symbol of the chromatic point group describing the 4-coloured tetrahedron becomes: 4'3'm'.
 |
In consequence of the symmetry decrease due to face colouring, the crystallographic point group from m3m becomes mmm, so that the 3-coloured cube can be described as a collection of three pinacoids; the symbol of the related chromatic point group is m3'm' since, unlike the chromatic secondary mirror planes m', the principal mirror planes m put in correspondence pairs of faces having an equal colour.
 |
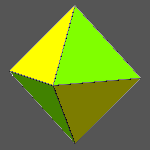 |
The symmetry decrease consequent to this alternative colouring turns out to be rather limited, since the point group, firstly m3m, becomes 43m. On the other hand, the chromatic point group turns out to be m'3m since, whereas the chromatic principal mirror planes m' reflect faces differently coloured, both 3-fold axes and secondary mirror planes m relate faces with an equal colour.
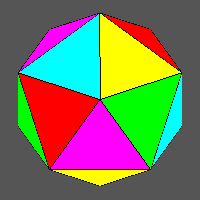 |
Of course the colours of the faces in the different groups are not independent, since each of the twenty faces belongs simultaneously to three of the twelve groups, as one can deduce from the relationship giving the total number of the faces:
(5x12)/3=20
All the faces having an equal colour are positioned like the faces of a tetrahedron, so that one can assume that the 5-coloured icosahedron is generated from the intersection of five different monochromatic tetrahedra.
The indicization of the faces belonging to every tetrahedron is not straightforward.
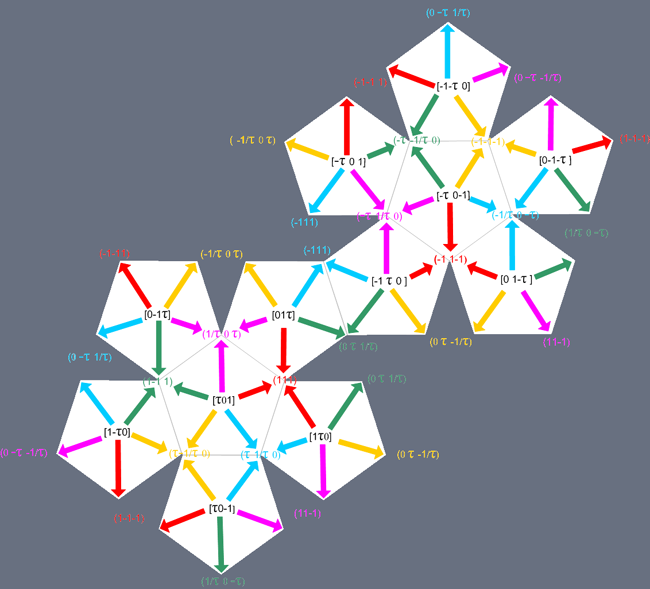
First of all, the indices of the 20 faces of the icosahedron derive from all possible permutations (8 and 12,
respectively) of the two different kinds of indices, both rational and irrational:
( 1 1 1 ) and (τ 1/τ 0)
where τ denotes the golden ratio.
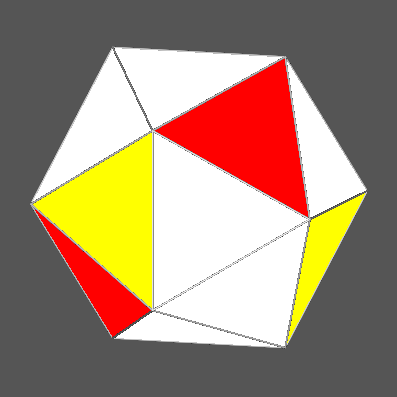
The tetrahedron whose faces (in red colour)
are characterized by the indices:
( 1 1 1 )
(111)
(11 1)
(1 1
1)
can be chosen as first tetrahedron A
 |
 |
( 1 1 1 ) ( 1 1 1 ) ( 1 1 1 ) ( 1 1 1 )
since these faces, together with the faces of the first tetrahedron, would give rise to a
As starting point for positioning the tetrahedron B (yellow), one can choose for example the ( 1 1 1 ) face; consequently to the application of a clockwise rotation of 44.48░ around the [ 1 1 1 ] direction, the three other faces of this tetrahedron, with the indices (111), (111) and (111), undergo a rotation of 41.81░, assuming the same position of the three faces of the icosahedron with the following indices : (τ -1/τ 0), (0 τ -1/τ ) and (-1/τ 0 τ ).
Such set of three faces, together with the initial ( 1 1 1 ) face, identifies a regular tetrahedron: actually the three faces form the same angle of 109.46░, characteristic of the regular tetrahedron, both each other and with the initial
 |
 |
For tetrahedron C
(green), the
rotation takes place around the direction perpendicular
to the
( 1 1 1 )
(111)
(111)
become:
(τ
-1/τ 0)
(0 τ 1/τ )
(1/τ 0 τ )
 |
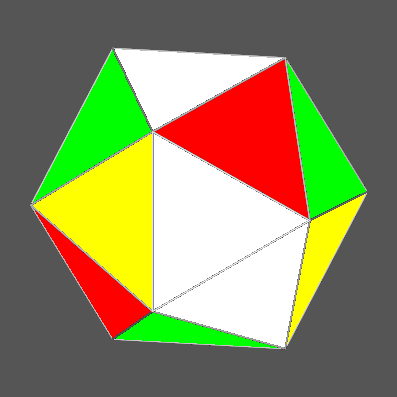 |
Analogously, for tetrahedron D (blue) the rotation takes place around the direction perpendicular to the
( 1 1 1 ) (111) ( 1 1 1 )
become:
(τ 1/τ 0) (0 τ 1/τ ) (-1/τ 0 τ )
 |
 |
Finally, for tetrahedron E (violet) the rotation takes place around the direction perpendicular to
(111) ( 1 1 1 ) (111)
become:
( τ 1/τ 0) (0 τ -1/τ ) (1/τ 0 τ)
 |
 |
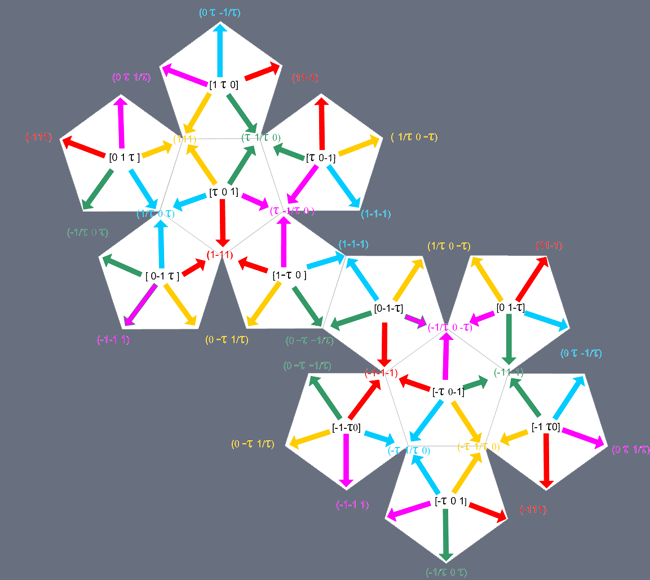
To summarize, the indices of the faces of the five tetrahedra whose intersection generates a 5-coloured icosahedron are reported in the following table.
| Colours | Indices of the faces | |||
| A (red) | (1 1 1) | (1 1 1) | (1 1 1) | (1 1 1) |
| B (yellow) | (1 1 1) | ( τ -1/τ 0 ) | (0 τ -1/τ ) | (-1/τ 0 τ ) |
| C (green) | (1 1 1) | ( τ -1/τ 0 ) | (0 τ 1/τ ) | (1/τ 0 τ ) |
| D (blue) | (1 1 1) | ( τ 1/τ 0 ) | (0 τ 1/τ ) | (-1/τ 0 τ ) |
| E (violet) | (1 1 1) | ( τ 1/τ 0 ) | (0 τ -1/τ ) | (1/τ 0 τ ) |
After any addition of a tetrahedron to the previous ones, it can be
interesting to examine carefully the polyhedra that originate in
correspondence of the intermediate steps leading from the initial tetrahedron to the final icosahedron.
In the following set of images one can see the five polyhedra (all in the same
orientation) sequentially formed by the intersection of the differently coloured tetrahedra.

In order to recognize the single forms making up the different polyhedra originated at each step and to identify the respective point group, it can be useful to orientate properly the different polyhedra, assigning an equal colour to all the faces belonging to each crystallographic form.
(clicking on the images below it is possible to visualize the corresponding VRML files )
 |
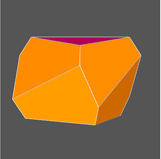 |
 |
 |
 |
- a trigonal trapezohedron (6 brown faces) and a pinacoid (2 fuchsia faces): 32 point group
- a trigonal trapezohedron (6 brown faces) and a rhombohedron (6 fuchsia faces): 32 point group
- a pentagon-dodecahedron (12 brown faces) and a tetrahedron (4 fuchsia faces): 23 point group
Concerning the colouring of the icosahedron by 5 colours, one must point out
that the previous solution is not unique: there is a second alternative,
leading to a colour distribution enantiomorphic (or chiral) to the first one.
This means that for the icosahedron there are two non-congruent distributions of the 5 colours:
in practice, equal colours are applied to the centro-symmetrical faces belonging to
the couple of chromatically chiral icosahedra.
Also in this second case it is possible to follow a procedure for face colouring analogous to the previous one.
The initial tetrahedron A'
(red), dual of the
red tetrahedron A belonging to the previous 5-coloured
icosahedron (let
us remember that the tetrahedron is autodual), this time will be the one whose faces have indices:
( 1 1 1 )
( 1 1 1 )
( 1 1 1 )
( 1 1 1 )
 |
 |
Each one of the other four tetrahedra will include only one of the four faces: Face colouring of the chiral icosahedron
(111) (111)
(111) (111)
belonging to the tetrahedron A.
The 44.48░ rotation (this time counterclockwise),
around the direction normal to one of the four faces of tetrahedron A,
implies a 41.81░ rotation of the three other faces of the tetrahedron A, leading
to a tetrahedron whose faces have, also in this case, the same orientation of
three faces of the icosahedron: the same color is attributed to the faces of
this new tetrahedron.
Repeating this procedure on each other face of tetrahedron A, one obtains the
following colour distribution, chiral of the previous one.
Colours
Indices of the faces
A' (red)
(1 1 1)
(1 1 1)
(1 1 1)
(1 1 1)
B'(yellow)
(1 1 1)
(τ 1/τ 0)
(0
τ 1/τ )
(1/τ 0
τ )
C'(green)
(1 1 1)
(τ 1/τ 0)
(0
τ -1/τ )
(-1/τ 0 τ )
D' (blue)
(1 1 1)
(τ -1/τ 0)
(0 τ -1/τ )
(1/τ 0 τ )
E' (violet)
(1 1 1)
(τ -1/τ 0)
(0 τ 1/τ )
(-1/τ 0
τ )
As already pointed out, from the two previous tables one can note that each face of whatever colour, having the indices (hkl) and belonging to an icosahedron, corresponds
to a face with the same colour and indices
In the following figure both the 5-coloured chiral icosahedron and the five tetrahedra
whose intersection generates such icosahedron are shown in the same orientation.

Rotating properly the image of the second icosahedron of the chromatically chiral pair, one can emphasize that the face colourings of the two icosahedra are symmetrical with respect to a vertical mirror placed between the two polyhedra put side by side.
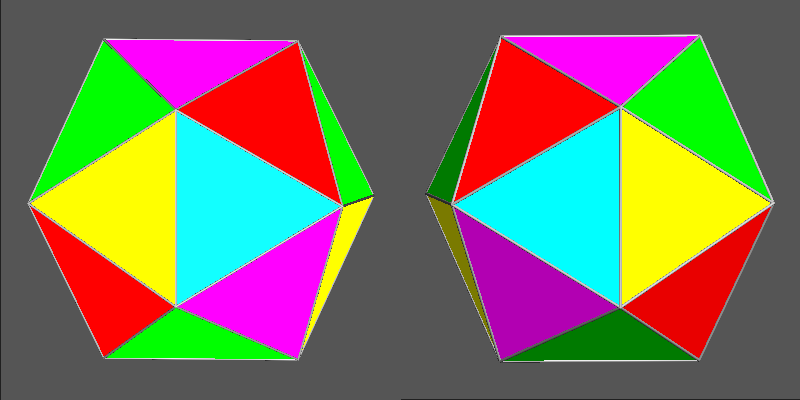
The difference between the two chiral colourings can be pointed out also by the nets of the chiral couple: in the following images one can ascertain that the face colouring is symmetrical with respect to a reflection line placed horizontally between the two nets (among the many possible alternative nets, the choice made concerns a kind of net showing that the icosahedron comes from a pentagonal euclidean antiprism, where each pentagonal base has been substituted by a pentagonal pyramid formed by five equilateral triangular faces).
|
The couple of chiral colourings of the 5-coloured icosahedron can be further highlighted remembering that, based on the duality icosahedron-dodecahedron, the
vertices of the dodecahedron correspond to the faces of the icosahedron, and so the
respective colourings. This can be pointed out by the net of
the dodecahedron, consisting of two groups, made of six pentagonal
faces, sharing a side: in each group the central face shares each side with another pentagonal face.
The coloured arrows show the colour of every vertex (shared by a set of three
pentagonal faces of the dodecahedron), corresponding to the colour of the dual face of the icosahedron.
|
The following is the net of the alternative chiral colouring, symmetrical of the previous one with respect to a vertical reflection line placed between the two nets put side by side.
|
Taking into account the face colouring, the symmetry of the icosahedron, which belongs to the m35 point group, results completely absent in the 5-coloured icosahedron. On the other hand, the symbol of the relative chromatic point group becomes m'3'5'.
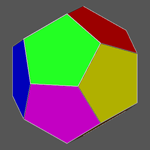 |
The use of six colours implies that a different colour characterizes each of the six pinacoids made up of pairs of parallel pentagonal faces: the crystallographic symmetry of the
Regarding the 4-coloured dodecahedron, the colouring procedure can be the following.
Let us consider one of the ten 3-fold axes of the dodecahedron, for example the one along the [111] direction. The angle between this direction and each perpendicular to the three nearest faces measures 37.38░. Such faces, with pentagonal shape, have in common a vertex placed along the 3-fold axis and share an edge in pairs: to optimize the visualization of these faces one needs to differentiate them, assigning to each face a different colour.
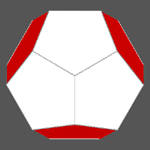 |
( τ 0 1 ) ( 0 1 τ ) ( 1 τ 0 )
Since these three faces do not share any edge or vertex, one can assign to them the same colour
The next step consists in considering the other three directions
that, together with
 |
( τ 0 1 ) ( 0 1 τ ) ( 1 τ 0 ),
whose perpendiculars form the above mentioned angle with the 3-fold axis aligned along the
 |
( τ 0 1 ) ( 0 1 τ ) ( 1 τ 0 ),
symmetrically placed around [1 1 1], which are added to the red and blue faces.
 |
( τ 0 1 ) ( 0 1 τ ) ( 1 τ 0 ),
The data relative to the 4-coloured dodecahedron are summarized in the following table.
| 4-coloured dodecahedron | ||||
| Colours of faces | Indices of faces | directions of 3-fold axis |
||
| A (red) | (τ 0 1 ) | ( 0 1 τ ) | ( 1 τ 0 ) | [1 1 1] |
| B (blue) | ( τ 0 1 ) | ( 0 1 τ ) | ( 1 τ 0 ) | [1 1 1] |
| C (yellow) | ( τ 0 1) | ( 0 1 τ ) | ( 1 τ 0 ) | [1 1 1] |
| D (green) | ( τ 0 1) | ( 0 1 τ ) | ( 1 τ 0 ) | [1 1 1] |
Also in the case of the 4-colour dodecahedron there is a second chiral distribution of the colours, to which one arrives following a procedure analogous to the previous one, and whose result is summarized in the relative table.
| 4-coloured chiral dodecahedron | ||||
| Colours of faces | Indices of faces | directions of 3-fold axis |
||
| A' (red) | ( τ 0 1) | (0 1 τ ) | (1 τ 0) | [1 1 1] |
| B' (blue) | ( τ 0 1) | (0 1 τ ) | (1 τ 0) | [1 1 1] |
| C' (yellow) | ( τ 0 1) | (0 1 τ ) | (1 τ 0) | [1 1 1] |
| D' (green) | ( τ 0 1) | (0 1 τ ) | (1 τ 0) | [1 1 1] |
Examining the two 4-coloured chiral dodecahedra along the four 3-fold axes previously
identified, one can note that they differ in the fact that, for each choice of
the colour assigned to the three "exterior" faces whose perpendiculars form an
angle of 79.19░ with a 3-fold axis, there is a permutation of the colours
assigned to the "interior" faces sharing a vertex placed along the
3-fold axis, with which the perpendiculars to such faces form an angle of 37.38░.
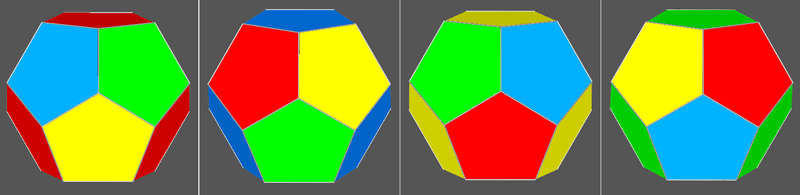 |
4-coloured dodecahedron |
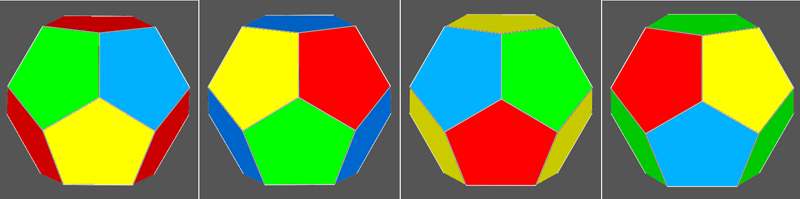 |
4-coloured chiral dodecahedron |
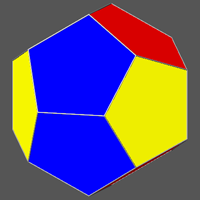 |
Whereas the previous colouring of the dodecahedron by 4 colours was completely asymmetric, the crystallographic symmetry of the 3-coloured dodecahedron corresponds to the mmm point group and the chromatic point group becomes m3'5'.
RHOMBIC DODECAHEDRON
Also in the case of the rhombic dodecahedron, using for example 4 or 6 different colours, one can
make sure that faces having the same colour do not share any edge or vertex.
 . . |
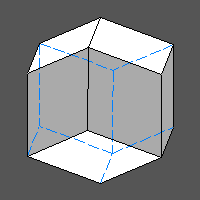 |
Also in this case it is worthwhile to refer to the directions corresponding to the 3-fold axes.
Six of the twelve rhombic faces of the rhombic dodecahedron belong to the zone of each 3-fold axis; in turn, each face belongs to two such zones, as it follows from the relationship:
 |
(110) (101) (011)
 |
(110) (101) ( 0 1 1 )
to which the red colour can be assigned.
 |
( 1 1 0 ) (011) (101)
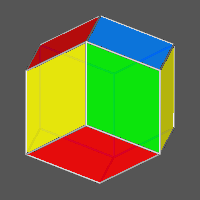 |
(110) (011) (101)
Summarizing, each colour is relative to the faces of a trigonal prism in zone with a 3-fold axis, which, like all the other symmetry operators present, is a chromatic simmetry operator, since it makes the connection between faces that are differently coloured. Therefore the 4-coloured rhombic dodecahedron turns out to be without any operator of crystallographic symmetry.
| 4-coloured rhombic dodecahedron | ||||
| Colours of faces | Indices of faces | directions of 3-fold axis | ||
| A (green) | (1 1 0) | (1 0 1) | (0 1 1) | [1 1 1] |
| B (red) | (1 1 0) | (1 0 1) | (0 1 1) | [1 1 1] |
| C (blue) | (1 1 0) | (0 1 1) | (1 0 1) | [1 1 1] |
| D (yellow) | (1 1 0) | (0 1 1) | (1 0 1) | [1 1 1] |
Assigning colour A' to the faces of the other trigonal prism belonging to the same zone of trigonal prism A and following the previous procedure to assign the other colours, a chiral colouring of the rhombic dodecahedron results.
| 4-coloured chiral rhombic dodecahedron | ||||
| Colours of faces | Indices of faces | directions of 3-fold axis | ||
| A' (green) | (1 1 0) | (1 0 1) | (0 1 1) | [1 1 1] |
| B' (red) | (1 1 0) | (1 0 1) | (0 1 1) | [1 1 1] |
| C' (blue) | (1 1 0) | (0 1 1) | (1 0 1) | [1 1 1] |
| D' (yellow) | (1 1 0) | (0 1 1) | (1 0 1) | [1 1 1] |
 |
The chromatic 3-fold axes present in the rhombic dodecahedron make the connection between the three tetragonal prisms by permutation of the colours.
Since in this case there is only sharing of vertices (and not of edges) between equally coloured faces of each tetragonal prism, the result of prism colouring in the
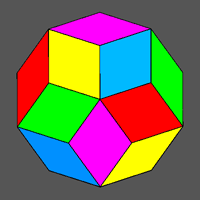 |
Since each rhombic face is shared between two groups of five faces, the overall number of faces in the triacontahedron, given by the relationship:
(12x5)/2=30 ,
is greater than the number of faces in the icosahedron where, as already seen, the overall number of faces is
Indices of two kinds (rational and irrational) lie with the faces of the triacontahedron; they result from all the cyclical permutations, change of sign included, of
Whereas it is immediate to realize that the 6 faces with indices of kind {100} have the same position of the faces of a cube, it is not as easy to realize that also among the remaining 24 faces one can identify 4 groups of 6 faces positioned like the faces of a cube.
Therefore the triacontahedron can be decomposed into five cubes, each one characterized by a different colour.
| Colour of each cube |
Indices of the faces | |||||
| A (violet) | (100) | (010) | (001) | (100) | (010) | (001) |
| B (red) | (τ 1 1/τ) | (1/τ τ 1) | (1 -1/τ τ) | (τ 1 -1/τ) | (-1/τ τ 1) | (1 1/τ τ) |
| C (blue) | (1 1/τ τ) | (τ 1 -1/τ) | (1/τ τ 1) | (1 -1/τ τ) | (τ 1 1/τ) | (-1/τ τ 1) |
| D (green) | (1/τ τ 1) | (τ -1 1/τ) | (1 1/τ τ) | (-1/τ τ 1) | (τ 1 -1/τ) | (1 -1/τ τ) |
| E (yellow) | (τ 1 -1/τ) | (1 -1/τ τ) | (-1/τ τ 1) | (τ 1 1/τ) | (1 1/τ τ) | (1/τ τ 1) |
|
In the following (clickable) figure, both the five cubes and a 5-coloured
triacontahedron generated from their intersection are shown in the same orientation. |
 |
 |
 |
 |
 |
 |
Analogously to the previous case of the 5-coloured icosahedron, also as regards the
5-coloured triacontahedron it is interesting to examine carefully the polyhedra that originate in
correspondence to the intermediate steps, consisting in the addition of a cube
to the previous ones and leading from the initial cube to the final triacontahedron.
In the following set of images one can see the five polyhedra (all in the same
orientation) sequentially formed by the intersection of the differently coloured cubes.

In order to recognize the single forms making up the different polyhedra originated at each step and to identify the respective point group, also in this case it can be useful to orientate properly the different polyhedra, assigning the same colour to all the faces that belong to each crystallographic form.
 |
 |
 |
 |
 |
The three forms, intermediate between cube (m3m point group) and rhombic triacontahedron (m35 point group), are made up of:
- a ditrigonal scalenohedron (12 brown faces): 3m point group
- a rhombohedron (6 brown faces), a rhombohedron (6 fuchsia faces) and a hexagonal prism (6 grey faces): 3m point group
- a diakisdodecahedron or diploid (24 brown faces): m3 point group
As one can see, only the polyhedron with eighteen faces consist of three forms: two different rhombohedra and a hexagonal prism.
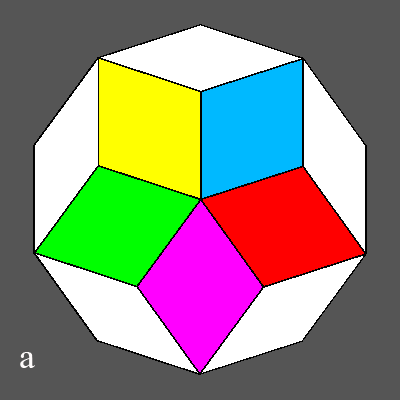
Operatively, to realize the colouring of the triacontahedron faces by 5 colours it is sufficient, after assignment of a specific colour to a pair of parallel faces, one picks the other two pairs of faces, both perpendicular to the first pair, with which they form a cube; alternatively one can follow the more elaborate procedure that will be described and illustrated in the four figures a-d.
Fig.a) Examining a triacontahedron
along the [τ01] direction, coinciding with a 5-fold axis where five
mirror planes are hinged, one can assume that the five faces, whose
perpendiculars form a 31.72░ angle with the 5-fold axis, belong to a
pentagonal deltohedron (also named antibipyramid, being the dual of a
pentagonal antiprism), 10-face polyhedron which symmetry is the one of point group
5m: a different colour has to be
assigned to each of the five vertex-sharing faces.
Also the perpendiculars to the other five faces of the deltohedron form a 31.72░
angle with the opposite [τ01] direction of the same 5-fold axis:
an equal colour will be assigned to the pairs of centrosymmetrical faces of the
two sets of five faces. Consequently, the same succession of colours, even if
in opposite clockwise and counterclockwise directions, characterizes the two sets of five faces belonging to the deltohedron.
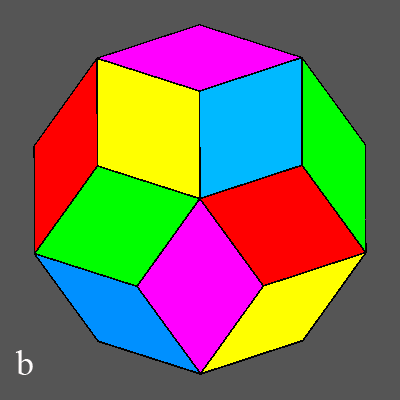
Fig.b) Again, regarding the same [τ01]
direction, one can assume that the other two sets of five rhombic faces,
whose perpendiculars form with the 5-fold axis a 58.28░ angle
(therefore greater than the previous one), belong to a second deltohedron.
In order to prevent equally coloured faces from sharing edges or vertices, the
colour assigned to each face of the second deltohedron will be the same of
the face, belonging to the adjacent set of five faces of the first
deltohedron and lying on the same mirror plane, that is the most distant.
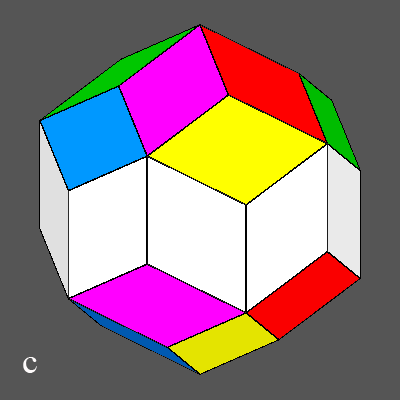
Fig.c) The same scheme of face
colouring is applied to the other set of five faces belonging to the second deltohedron.
Fig.d) At this point there is nothing
left to do but to assign a colour to the last ten faces that, being in zone with
the 5-fold axis parallel to [τ01] direction, form a decagonal prism. The
condition that faces equally coloured cannot share edges and vertices
identifies univocally the colour of every face of the decagonal prism.
Unlike the 5-coloured icosahedron and the 4-coloured dodecahedron, for the 5-coloured triacontahedron
there is not any alternative of a chiral colouring, since such colouring is intrinsecally centrosymmetrical.
The possibility of colouring a triacontahedron by only three colours, without sharing
of edges between equally coloured faces, was pointed out by John Dalbec to George Hart, who described it in his already cited page:
The 2-fold axis perpendicular to the central face of each chain relates to each other the
two
lateral faces, both connected through a vertex to the central face. The
action of the other 2-fold axes perpendicular to the first 2-fold axis
relates the two lateral faces of the first chain to the two lateral faces of the second
chain having the same colour: the collection of these four faces makes up a rhombic
bisphenoid.
Finally, in the following summarizing table the
different colourings of polyhedra are listed, together with the indication of a possible chiral distribution of
the colours.
http://www.georgehart.com/virtual-polyhedra/colorings.html
Each colour (red,
green and
blue)
characterizes a pair of chains made of five rhombic faces connected through
vertices. Adding in succession the green and blue chains to the red ones, one
obtains the complete colouring of the triacontahedron by only three colours as shown in the following clickable images.
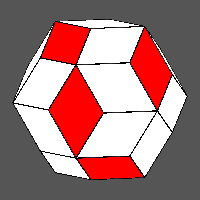


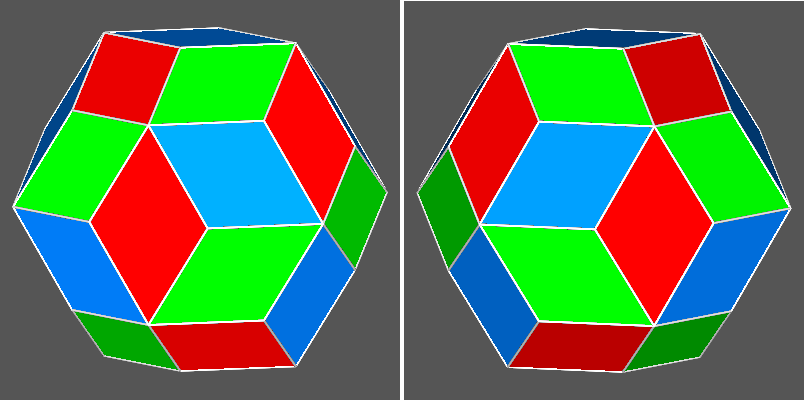
Since three perpendicular 2-fold axes pass through the centres of the
pairs of central face of the chains, in the absence of any further symmetry operator
for this arrangement of coloured faces, 222 will be the point group (subgroup of the m35
icosahedral point group) to which the 3-coloured triacontahedron belongs. In addition, the lack both of
mirror planes
and inversion centre implies the existence of two alternatives for the face colouring.
Also in this case, by an appropriate rotation of the image of the second
3-coloured triacontahedron it is possible to highlight the fact that colourings of the faces that belong to the two
chiral triacontahedra are symmetric with respect to a vertical plane placed between the two polyhedra put side by side.
Analogously, the action of the set of three 2-fold axes over the faces placed at
the end of the
same chain
generates a rhombic bisphenoid
oriented differently, but identical to the previous one; consequently, in the 3-coloured triacontahedron two
rhombic bisphenoids and a pinacoid are present for each pair of equally
coloured chains: hence there are a total of six rhombic bisphenoids and three pinacoids.
Therefore nine colours
would be necessary to differentiate completely the crystallographic forms altogether present.
The following image shows, all in the same orientation, the single forms
(three pinacoids, making up a 3-coloured cubes, and six rhombic bisphenoids)
whose intersection corresponds to the central 9-colour rhombic triacontahedron. 
The last three columns report respectively:
ALTERNATIVE CHOICES for POLYHEDRA COLOURING | |||||
|
n-coloured polyhedron |
n colours | Chirality of n-coloured polyhedron |
Point group of polyhedron |
Point group of n-coloured polyhedron |
Chromatic point group of n-coloured polyhedron |
| Tetrahedron | 4 | yes | 43m | 1 | 4'3'm' |
| Cube | 3 | no | m3m | mmm | m3'm' |
| Octahedron | 4 | no | m3m | 1 | m'3'm' |
| Octahedron | 2 | no | m3m | 43m | m'3m |
| Icosahedron | 5 | yes | m35 | 1 | m'3'5' |
| Dodecahedron | 6 | no | m35 | 1 | m'3'5' |
| Dodecahedron | 4 | yes | m35 | 1 | m'3'5' |
| Dodecahedron | 3 | no | m35 | mmm | m3'5' |
| Rhombic dodecahedron | 6 | no | m3m | 1 | m'3'm' |
| Rhombic dodecahedron | 4 | yes | m3m | 1 | m'3'm' |
| Rhombic dodecahedron | 3 | no | m3m | mmm | m3'm' |
| Rhombic triacontahedron | 5 | no | m35 | 1 | m'3'5' |
| Rhombic triacontahedron | 3 | yes | m35 | 222 | m'3'5' |
ACKNOWLEDGEMENTS
Many thanks are due to Maria
Rosa Ardigo' for the fruitful discussions and to Fabio Somenzi for his help
concerning the translation of the text.
LINKS
-
http://www.georgehart.com/virtual-polyhedra/vp.html
-
http://www.georgehart.com/virtual-polyhedra/platonic-info.html
-
http://www.georgehart.com/virtual-polyhedra/archimedean-info.html
-
http://www.georgehart.com/virtual-polyhedra/archimedean-duals-info.html
- http://www.georgehart.com/virtual-polyhedra/colorings.html
-
http://mathworld.wolfram.com/topics/PlatonicSolids.html
-
http://mathworld.wolfram.com/ArchimedeanSolid.html
- http://mathworld.wolfram.com/topics/DualPolyhedra.html
- http://en.wikipedia.org/wiki/Polyhedra#Uniform_polyhedron
SUGGESTED LECTURES