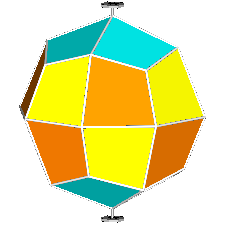
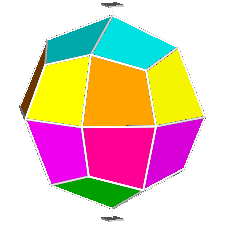
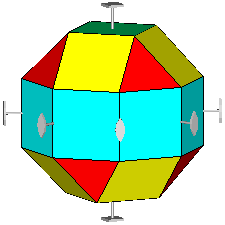
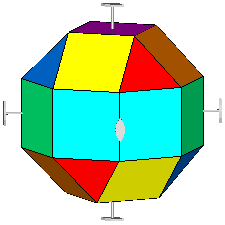
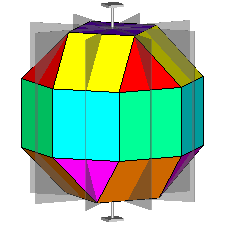
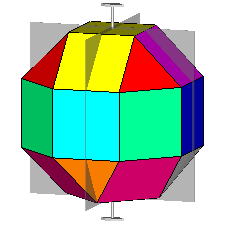
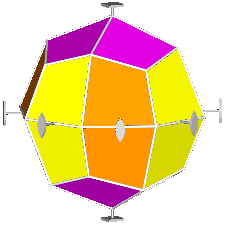
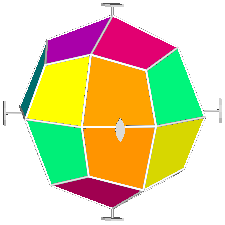
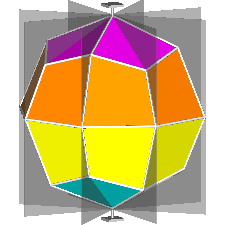
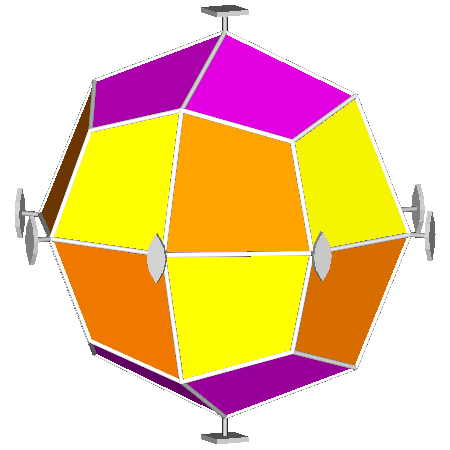
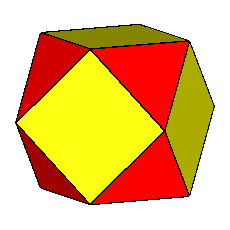
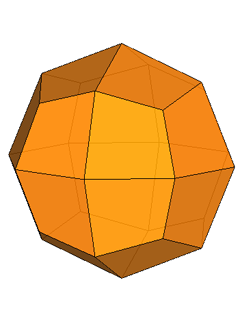
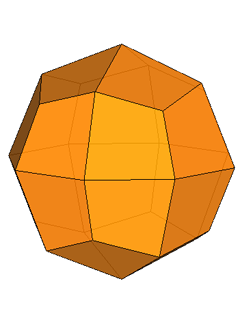
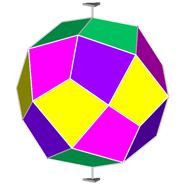
The rhomb-icosidodecahedron has four other
isomers, whereas icosidodecahedron, cuboctahedron and
rhomb-cuboctahedron have only one other isomeric
form. Particularly noteworthy in case of the rhomb-cuboctahedron, since all its solids angles are congruent.
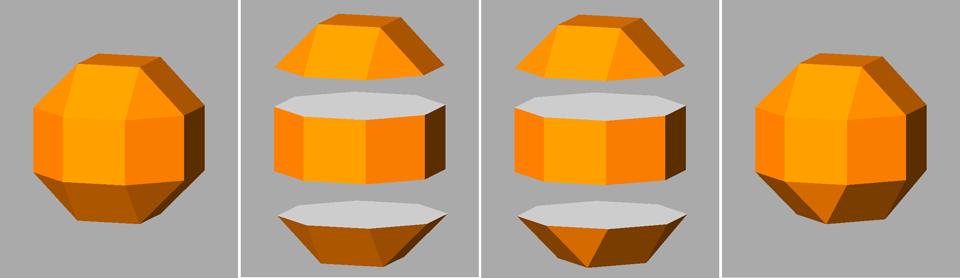
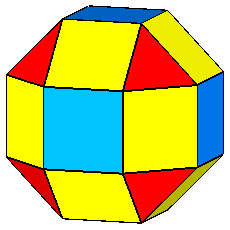
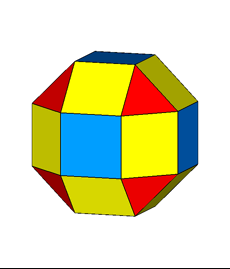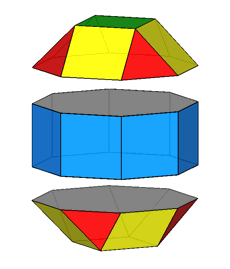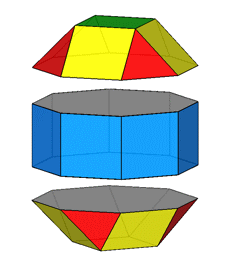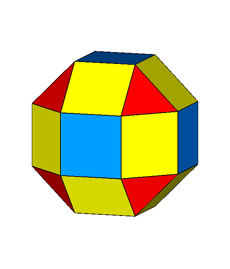
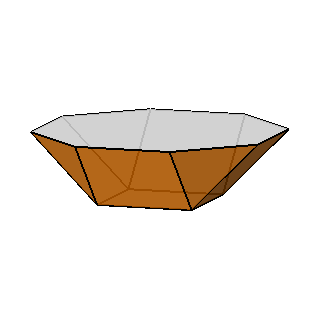
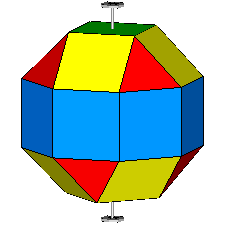
Focusing our attention on the rhomb-cuboctahedron, its dissection into
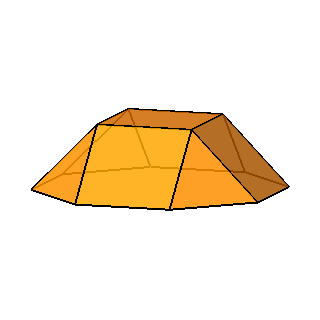
elementary polyhedra gives an octagonal prism and two square cupolas (Fig.3). A square cupola includes two
parallel polygons, a square and an octagon, connected
by a ring of other eight polygons, where squares alternate to equilateral
triangles. Both squares and triangles of the ring share one side with the
octagon, whereas the opposite side (in case of the squares) or vertex (in case
of the triangles) are shared with the
square parallel to the octagon.
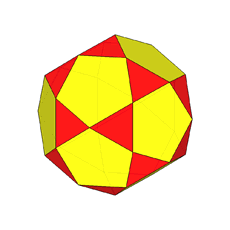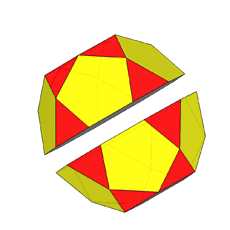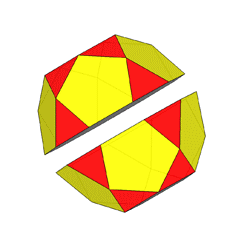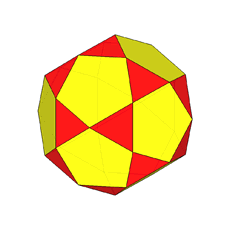
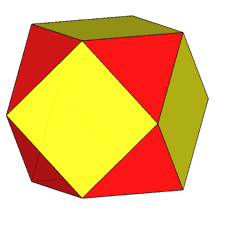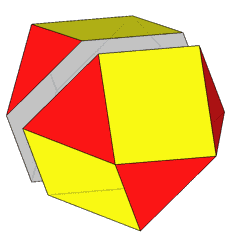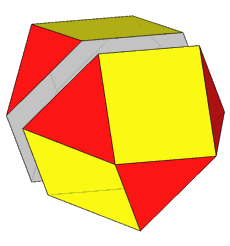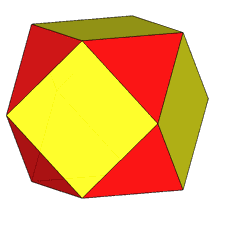
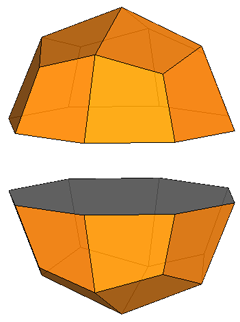
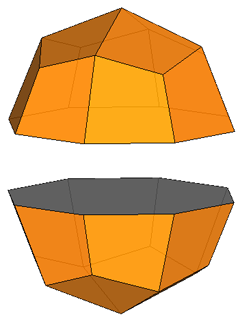
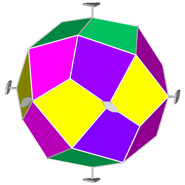
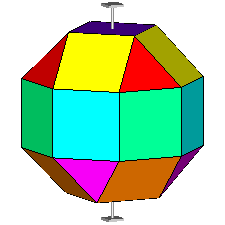
If, after the rhomb-cuboctahedron dissection, one of the two cupolas is rotated
by 45° and then the polyhedron is reassembled, the resulting form is the
pseudo rhomb-cuboctahedron: the two forms, made of the same faces, are isomers
(Fig.4).
|
|
Fig.4 - Dissection of the rhomb-cuboctahedron in
regular-faced polyhedra, 45° rotation of the lower square cupola and subsequent
reassembly leading to the pseudo rhomb-cuboctahedron.
|
In addition to pseudo rhomb-cuboctahedron and Miller's solid, a further name,
deriving from Johnson's nomenclature and showing how the solid can be built
starting just from regular-faced elementary polyhedra, is elongated square gyrobicupola, since it includes two square cupolas, reciprocally rotated of 45° (gyro)
and separated by an octagonal prism, which makes the resulting form more elongated
than a square gyrobicupola (if one applies the same nomenclature to the Archimedean solids,
an alternative name of the rhomb-cuboctahedron could be elongated square bicupola).
Two nets of the rhomb-cuboctahedron (left) and
pseudo rhomb-cuboctahedron (right) are shown in Fig.5: in
the rhomb-cuboctahedron a square of each cupola is connected, on opposite sides,
to the same square of the octagonal prism, whereas in the pseudo
rhomb-cuboctahedron similar squares, belonging to the two cupolas, are connected (always on opposite
sides) to contiguous squares of the octagonal prism.
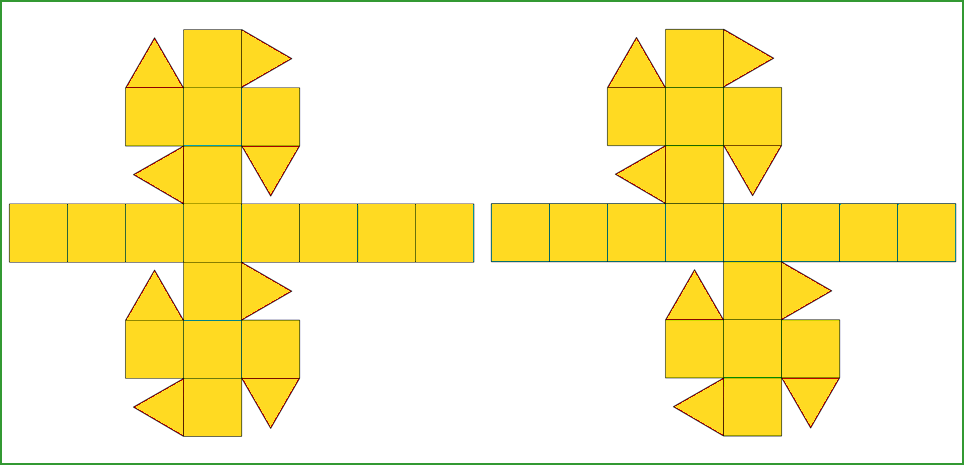 |
Fig.5 - Nets of the rhomb-cuboctahedron (left) and pseudo rhomb-cuboctahedron (right);
clicking here
one can see alternative coloured nets of the two isomers. |
The comparison of the rhomb-cuboctahedron
with the pseudo rhomb-cuboctahedron (henceforth, RCO and pseudo-RCO)
lets to highlight the differences between the two solids.
-
All the vertices of RCO and pseudo-RCO, equidistant from the centre of the
respective polyhedron, are shared by four faces (three squares and a triangle): the solid angles are all congruent.
-
The initial and final
positions of the RCO coincide if one applies, perpendicularly to each pair of parallel faces, a rotation of:
- 120° in case of the eight triangular faces
- 180° in case of the twelve square faces sharing edges with the triangular faces
- 90° in case of the other six square faces
-
With respect to all its faces, the pseudo-RCO shows the same behaviour only for a 90° rotation
along a direction perpendicular to the square bases of the two cupolas resulting from the dissection.
Moreover, it is invariant also in case of a rotation along four 2-fold axes perpendicular both to the
previous direction and to the edges between the square faces of the octagonal prism.
-
In addition, mirror planes are also present:
nine in RCO and four in pseudo-RCO; in turn, the centre of symmetry is present only in RCO.
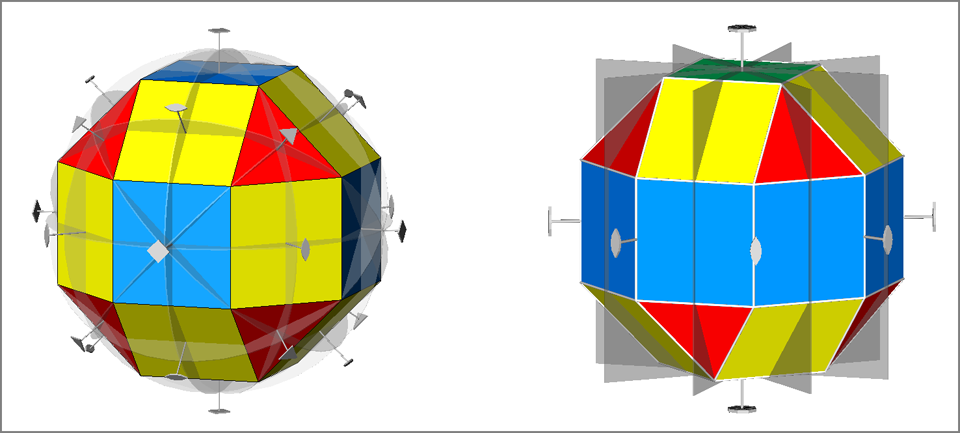
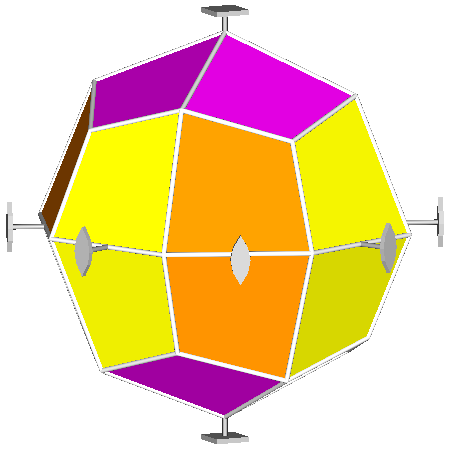
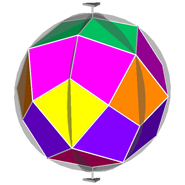
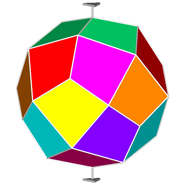
Then, in order to detect all the different features, it is opportune to draw RCO and
pseudo-RCO showing their symmetry operators and attributing different colours to each single form
(Fig.6).
(clicking on the images one can visualize the corresponding VRML files)
|
|
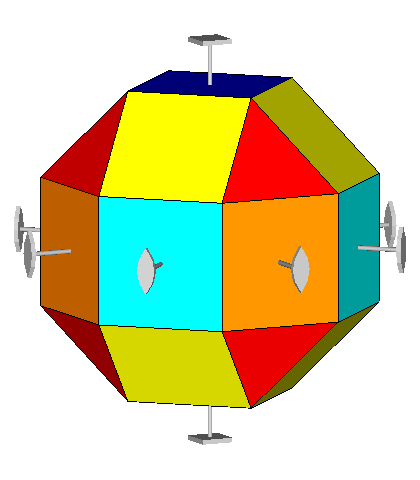
Fig.6 - Rhomb-cuboctahedron (on the left) and pseudo rhomb-cuboctahedron (on the right) drawn with their respective symmetry operators,
namely mirrors, rotation and roto-inversion axes.
|
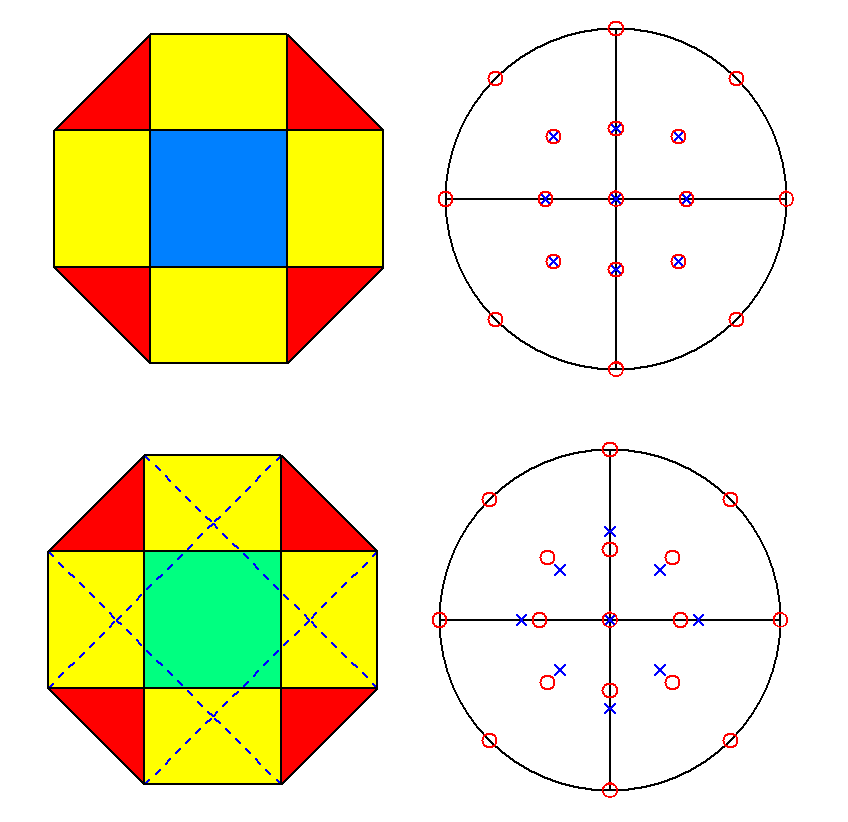
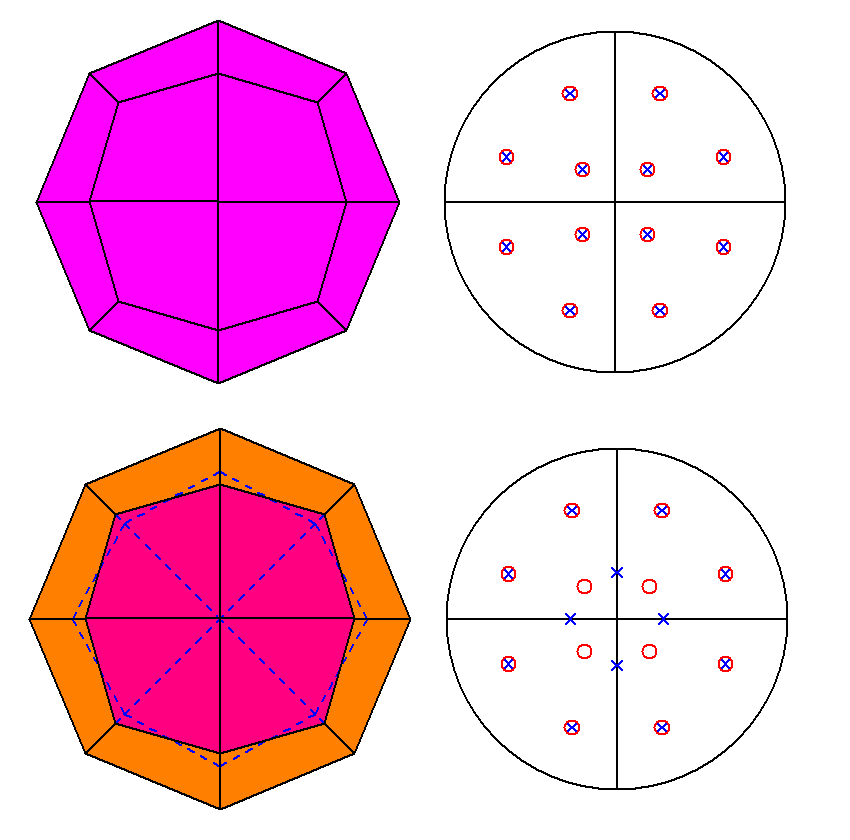
The views along the [001] direction of RCO and pseudo-RCO
and the stereographic projections of their faces are shown in Fig.7,
emphasizing that the faces belonging to the two cupolas are superimposed only
in RCO.
 |
|
Fig.7 - View along the [001] direction and relative stereographic
projection of rhomb-cuboctahedron (upper row) and pseudo rhomb-cuboctahedron (lower row). |
The symbol of the symmetry group to which RCO belongs is
Oh in the Schoenflies notation
and
m3m in the International notation.
Finally, adopting the more explicit extended notation, it becomes
4/m
3 2/m.
The last notation highlights the presence of mirror
planes orthogonal both to 4-fold and 2-fold rotation axes, in addition to 3-fold
rotoinversion axes (it must be remembered that the action of an odd
rotoinversion axis is equivalent to the disjoint action of the corresponding
odd rotation axis and the centre of symmetry). In total there are 24
symmetry elements (if one includes also identity):
three pairs made of a 4-fold rotation axis and an orthogonal mirror m
six pairs made of a 2-fold rotation axis and an orthogonal mirror m
four 3-fold rotation axes
centre of symmetry
identity
In the Schoenflies notation, D4v is the symbol of the symmetry group
relative to the pseudo-RCO, whereas in the International notation it is
8m2, indicating that the four mirror planes
present in the pseudo-RCO, at 45° from each other, intersect along a line that
is not only a 4-fold rotation axis, but also a
8-fold rotoinversion axis (equivalent to a 8-fold rotoreflection axis).
Orthogonally to the 8-fold rotoinversion axis and symmetrically interposed between the mirrors,
there are also four 2-fold rotation axes. The absence of the centre of symmetry implies that the mirror planes are not orthogonal
to the even-fold rotation axes of the pseudo-RCO.
At this point one can ascertain that in
RCO the action of the symmetry operators makes all the vertices equivalent:
for example, each 3-fold rotation axis, orthogonal to a triangle, relates the
three vertices of the triangle itself.
In pseudo-RCO, on the contrary, only two vertices of each triangle are related by a mirror,
whereas there is no symmetry operator relating the third vertex (the
one at a corner of the square basis of the cupola) to the others.
Therefore, concerning the isomeric couple consisting of RCO and
pseudo-RCO, only RCO is vertex-transitive (like all the other
Archimedean solids). It can be useful to recall the definition given by Peter R. Cromwell [3]:
"A polyhedron is vertex-transitive (or isogonal) if any vertex can be carried to any other by a symmetry operation".
Consequently, the lack of vertex-transitivity is the objective property that,
added to aesthetical reasons, prevents pseudo-RCO from being numbered among the Archimedean solids.
In other words, according to Viktor A. Zalgaller [7]:
"Besides two infinite series of prisms and antiprisms, ... there further
exist only 13 semiregular polyhedra (the bodies of Archimedes). If instead
of the compatibility of the vertices under selfcoincidence of the polyhedron
as a whole, we require only the local commonness of the vertices, then here
one more, the fourteenth, polyhedron exist."
DUALS OF THE RHOMB-CUBOCTAHEDRON AND THE PSEUDO RHOMB-CUBOCTAHEDRON
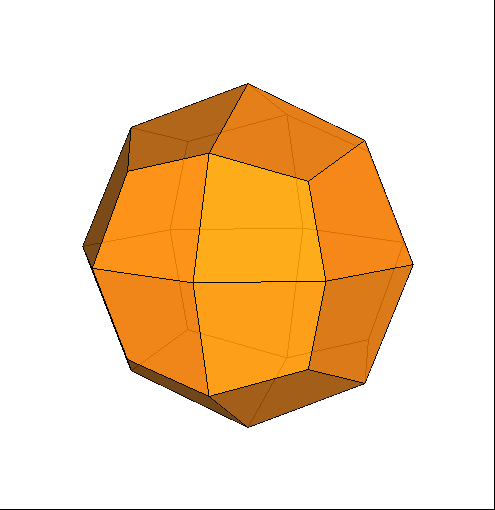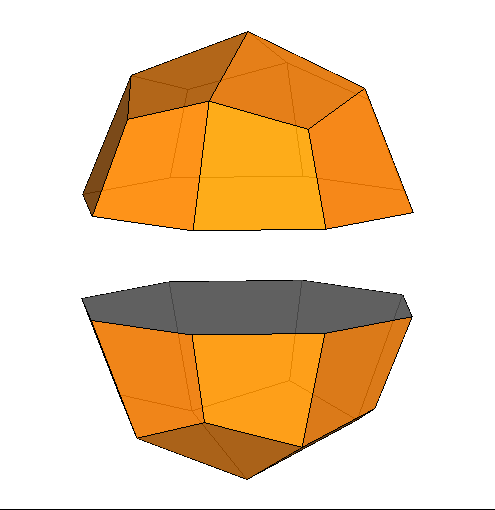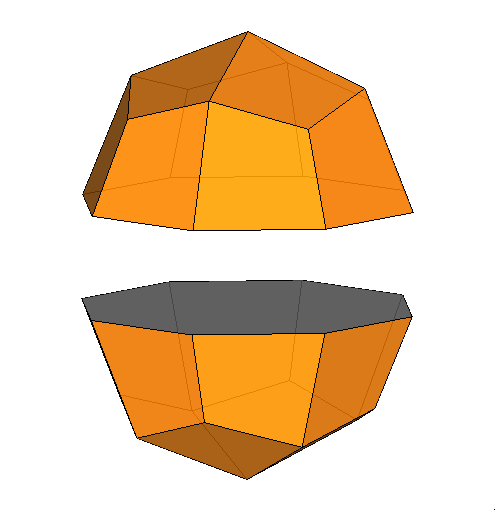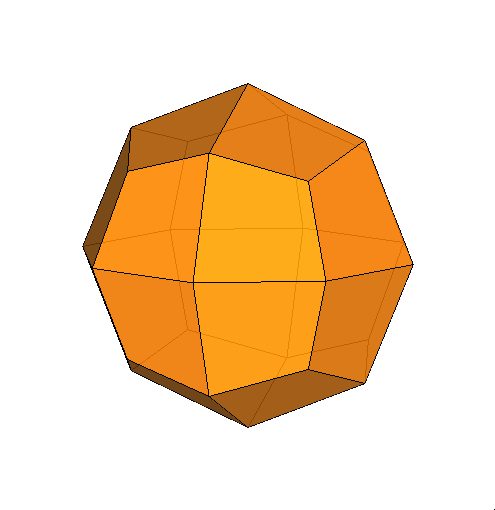
|
|
Fig.8 - Animation showing the transition from the Catalan
deltoid-icositetrahedron, dual of rhomb-cuboctahedron, to the dual of the pseudo
rhomb-cuboctahedron, by a 45° rotation of the lower half of the polyhedron.
|
The transition from the dual of RCO to the dual of pseudo-RCO
can be accomplished by the following steps (Fig.9):
split of the first dual in two halves
45° rotation of the lower halfreassembly of the two parts of the solid
In common, the twenty-four faces of both duals of RCO and pseudo-RCO
have
an equal distance from the centre of the respective solid and an identical shape (they are all kite-shaped),
whereas their different features derive from the vertex transitivity of the RCO alone.
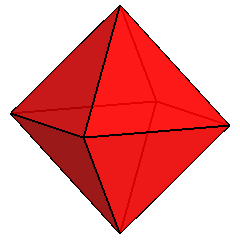
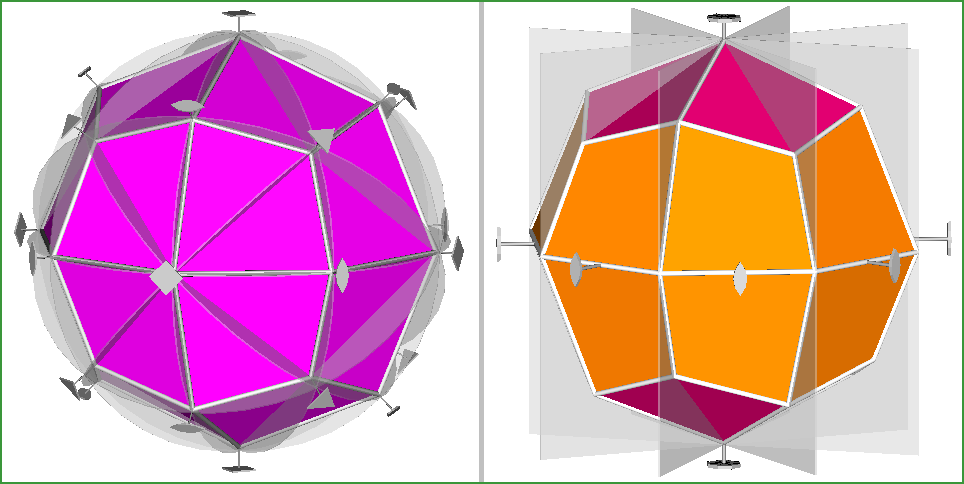
The dual of the Archimedean RCO is obviously a Catalan solid, named
deltoid-icositetrahedron (or trapezohedron), belonging to m3m,
the same point group of RCO: by the action of the relative symmetry operators, one face can be related to all the others.
From a crystallographic point of view, the form, made of 24 kite-shaped (or
deltoidal) faces, can be identified by the generalized Miller's indices
{1.1.√2+1}.
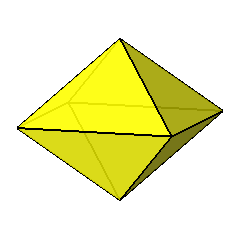
The pseudo-RCO and its unnamed dual belong to the same point
group,
8m2, whose symmetry operators
are instead unable to relate one vertex to all the other, in case of
pseudo-RCO, and one face to all the others, in case of its dual.
It follows that the deltoid-icositetrahedron, like all the Catalan solids, is
face-transitive or isohedral (according again to Peter R. Cromwell [3]: "A polyhedron is said to
be face transitive if for any pair of faces, there is a symmetry of the
polyhedron which carries the first face onto the second"), whereas the
dual of the pseudo-RCO is not face transitive: as described in the next chapter, it can be derived from the intersections
of two single forms, having obviously a lower molteplicity.
In Fig.10 the duals of RCO and pseudo RCO are shown with their symmetry operators.
(clicking on the images one can visualize the corresponding VRML files)
|
Fig.10 - The {1 1 √2+1}
Catalan deltoid-icositetrahedron, dual of the Archimedean rhomb-cuboctahedron (left) and the dual of pseudo rhomb-cuboctahedron
(right), drawn with the symmetry operators relative to m3m and
8m2 point groups, respectively.
|
The views along the [001] direction of the duals of RCO and pseudo-RCO and the
stereographic projections of their faces are shown in
Fig.11,
emphasizing that, in case of the dual of pseudo-RCO, not all the faces are superimposed.
 |
|
Fig.11 - View along the [001] direction, and relative stereographic projection,
of the Archimedean deltoid-icositetrahedron, dual of rhomb-cuboctahedron
(upper row), and the dual of pseudo rhomb-cuboctahedron (lower row). |
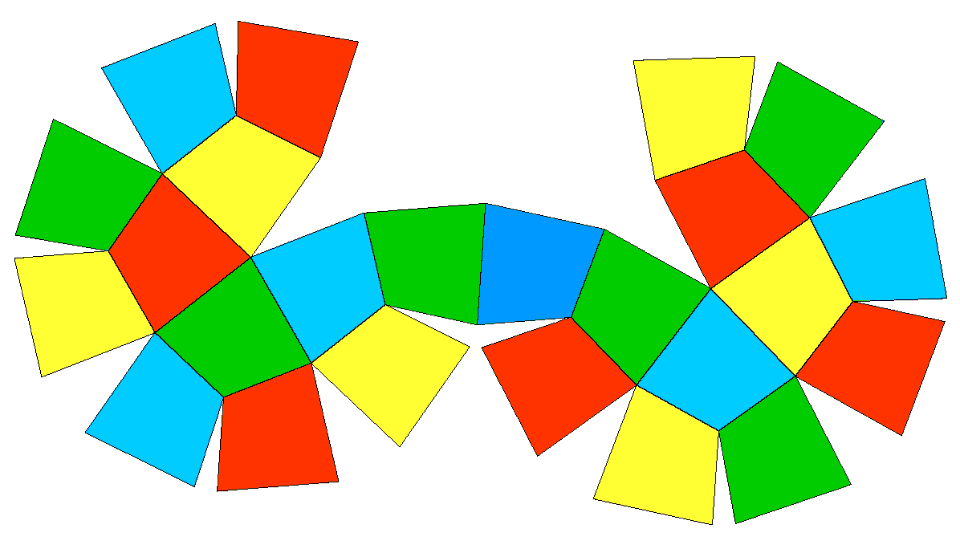
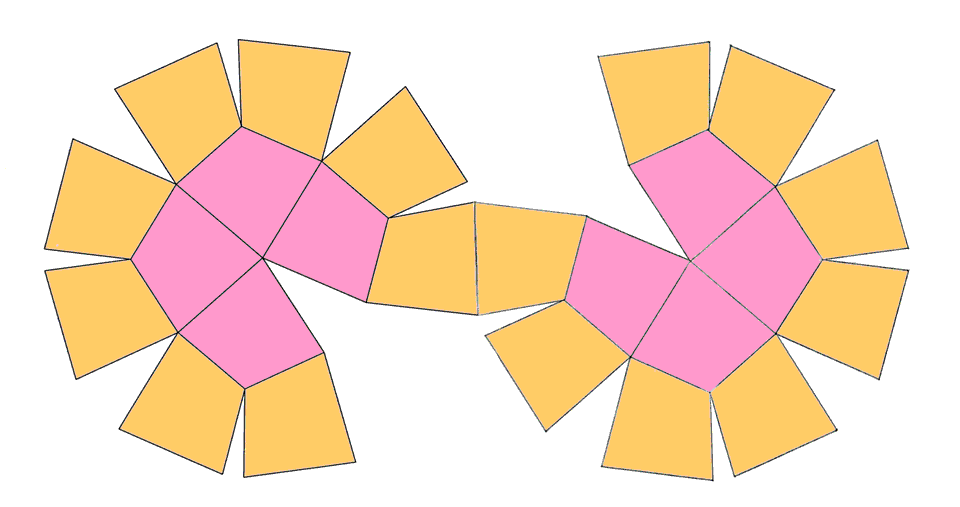
The nets of the
duals of RCO and pseudo-RCO are shown in
Fig.12.
 |
 |
|
Fig.12 - Four-coloured net of deltoid-icositetrahedron, dual of
rhomb-cuboctahedron and two-coloured net of the dual of pseudo rhomb-cuboctahedron. |
DECOMPOSITION OF RHOMB-CUBOCTAHEDRON, PSEUDO RHOMB-CUBOCTAHEDRON AND
THEIR DUALS IN SINGLE FORMS
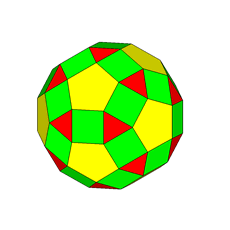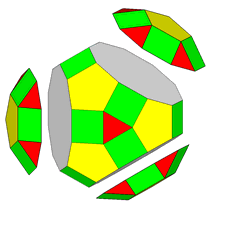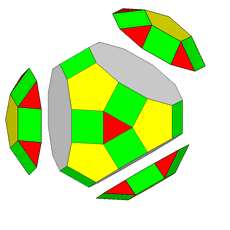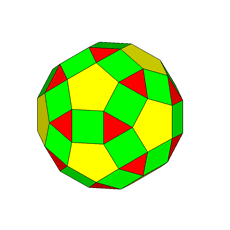
In Fig.13 the dual of the pseudo RCO (central image) is
decomposed into two single forms, an octagonal bipyramid (on the left) and a tetragonal kite-shaped isosceles trapezohedron (or deltohedron)
on the right, both compatible with the
8m2 point group to which also
the pseudo RCO belongs.
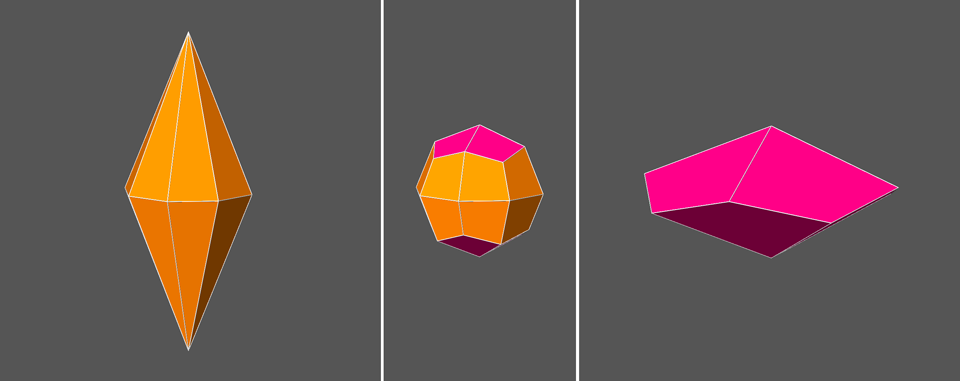 |
Fig.13 - Scale views of the {√2+1 1 1} octagonal bipyramid (left) and
the {1 1 √2+1} tetragonal deltohedron
(right), whose intersection generates the dual of the pseudo rhomb-cuboctahedron
(centre) when the ratio of their cental
distances takes a proper value. The values of the indices have been
calculated in relation to a monometric set of three orthogonal reference
axes.
|
On the other hand, the deltoid-icositetrahedron being face transitive, it is not
further decomposable in
m3m
point group.
Taking a backward step, since both RCO and pseudo-RCO are
not face transitive, they can be decomposed (Fig.14)
in different single forms
that, taking into account the respective m3m
and 8m2 point groups, are:
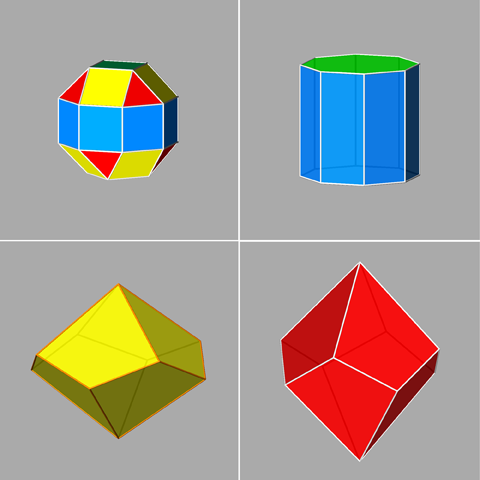
a cube, an octahedron and a rhomb-dodecahedron for RCO
an octagonal prism, a pinacoid and two 4-fold isosceles trapezohedra (or deltohedra) for pseudo-RCO.
Conversely, the intersection of such single forms, placed at appropriate
distances from the centre of the polyhedron, re-build RCO and pseudo-RCO.
 |
 |
|
Fig.14 - From the decomposition of a rhomb-cuboctahedron in single
forms (left), one obtains a cube, an octahedron and a rhomb-dodecahedron,
whereas the pseudo rhomb-cuboctahedron (right) gives an octagonal prism,
a pinacoid and two different 4-fold deltohedra (isosceles trapezohedra with
kite-shaped faces). The indices of the two deltohedra are {101} and {111},
if one assumes a monometric set of three orthogonal reference axes. |
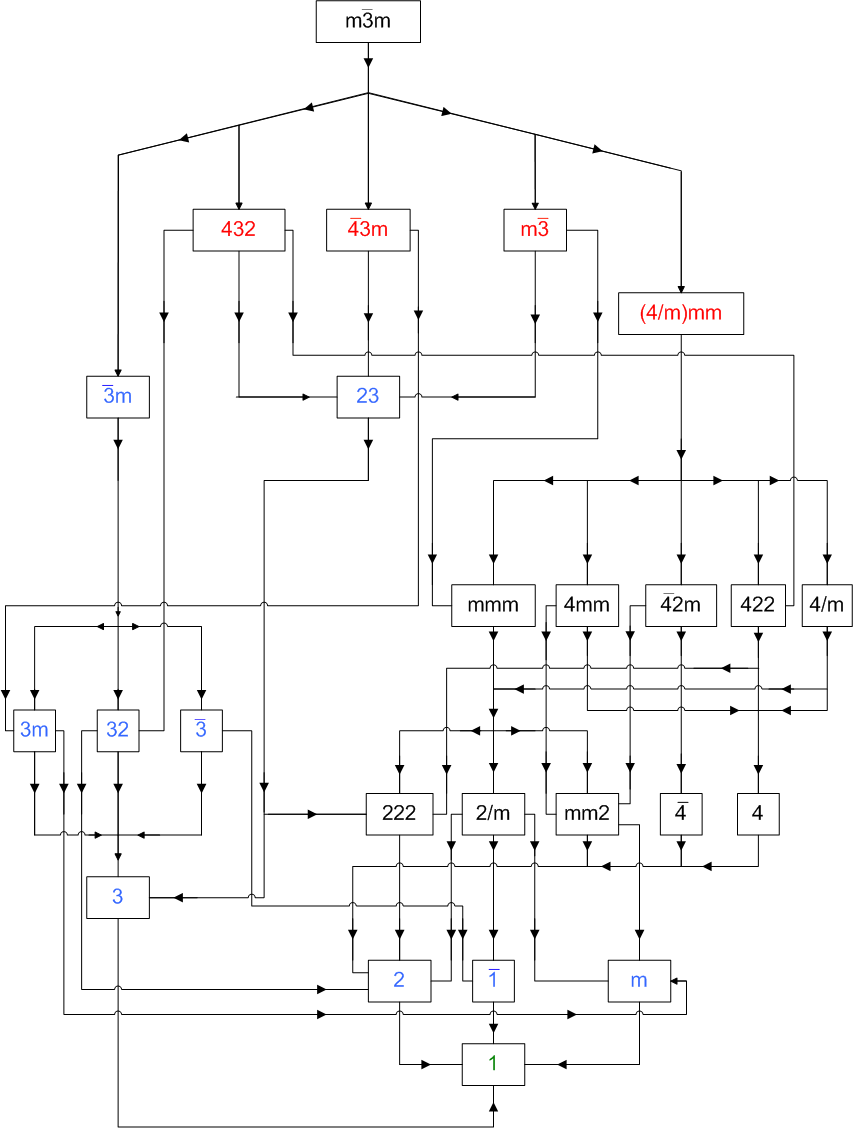
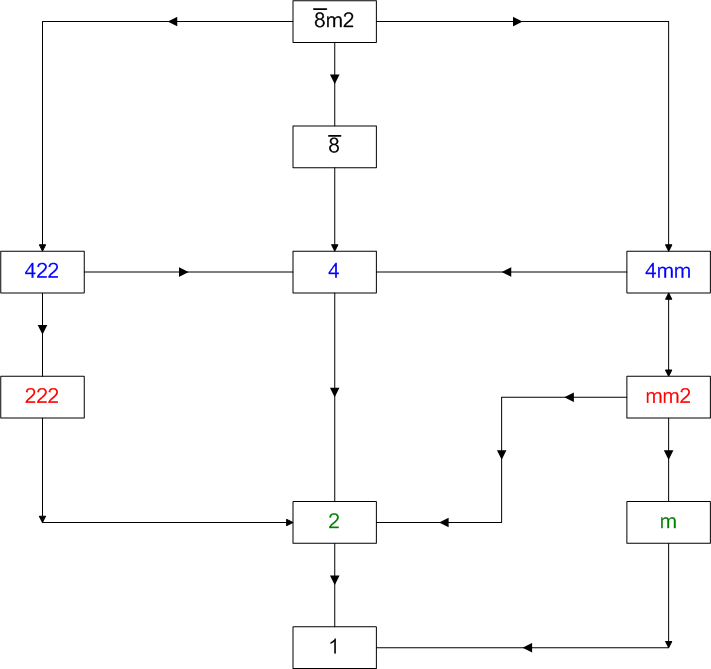
It may be interesting to visualize the single forms originating from
the decomposition of RCO, pseudo-RCO and their duals in the different point
groups which are subgroups of m3m
or 8m2 (Fig.15
and Fig.16, respectively).
Fig.15 - Flow chart showing the subgroups of cubic m3m point group.
Fig.16 - Flow chart showing the subgroups of 8m2 point group.
The subgroups belonging to monoclinic and triclinic systems,
the ones with the lowest symmetry, have not been taken into consideration
concerning the visualization of the forms relative to such subgroups.
The decomposition of the rhomb-cuboctahedron and the deltoid-icositetrahedron,
its dual, into single forms belonging to point subgroups of m3m
is shown in Fig.17.
|
Decomposition of the rhomb-cuboctahedron and
the deltoid-icositetrahedron, its dual, into sets of forms with
lower symmetry, belonging to cubic, trigonal, tetragonal and orthorhombic point
groups, all subgroups of the m3m point group
|
|
1 cube (6)
1 octahedron (8)
1 rhomb-dodecahedron (12) |
1 cube (6)
1 octahedron (8)
1 rhomb-dodecahedron (12) |
1 cube (6)
1 octahedron (8)
1 rhomb-dodecahedron (12) |
1 cube (6)
2 tetrahedra (4)
1 rhomb-dodecahedron (12) |
1 cube (6)
2 tetrahedra (4)
1 rhomb-dodecahedron (12) |
| m3m |
432 |
m3 |
43m |
23 |
|
1
deltoid-icositetrahedron(24) |
1
deltoid-icositetrahedron(24) |
1
deltoid-icositetrahedron(24) |
2 triakis-tetrahedra (12) |
2 triakis-tetrahedra (12) |
|
3 rhombohedra (6)
1 hexagonal prism (6)
1pinacoid (2) |
3 rhombohedra (6)
1 hexagonal prism (6)
1pinacoid (2) |
3 rhombohedra (6)
2 trigonal prisms (3)
1pinacoid (2) |
6 trigonal pyramids (3)
1 hexagonal prism (6)
2 pedions (1) |
6 trigonal pyramids (3)
2 trigonal prisms (3)
2 pedions (1) |
| 3m |
3 |
32 |
3m |
3 |
|
2 rhombohedra (6)
1 ditrigonal scalenohedron (12) |
4 rhombohedra (6) |
4 rhombohedra (6) |
4 trigonal pyramids (3)
2 ditrigonal pyramids (6) |
8 trigonal pyramids (3) |
|
2 tetragonal bipyramids
(8)
2 tetragonal prisms (4)
1 pinacoid (2) |
2 tetragonal bipyramids
(8)
2 tetragonal prisms (4)
1 pinacoid (2) |
2 tetragonal bisphenoids
(4)
1 tetragonal bipyramid (8)
2 tetragonal prisms (4)
1 pinacoid (2) |
2 tetragonal bisphenoids
(4)
1 tetragonal bipyramid (8)
2 tetragonal prisms (4)
1 pinacoid (2) |
| (4/m)mm |
422 |
4m2 |
42m
|
|
1 bipyramid ditetragonal
(16)
1 bipyramid tetragonal (8) |
2 tetragonal trapezohedra (8)
1 bipyramid tetragonal (8) |
2 tetragonal bisphenoid
(4)
2 tetragonal scalenohedra (8) |
2 tetragonal bisphenoid
(4)
2 tetragonal scalenohedra (8) |
|
4 pyramid tetragonal (4)
2 tetragonal prisms (4)
2 pedions (1) |
2 tetragonal bipyramids
(8)
2 tetragonal prisms (4)
1 pinacoid (2) |
4 bisphenoids (4)
2 tetragonal prisms (4)
1 pinacoid (2) |
4 pyramid tetragonal (4)
2 tetragonal prisms (4)
2 pedions (1) |
| 4mm |
4/m |
4 |
4
|
|
2 pyramid ditetragonal (8)
2 pyramid tetragonal (4) |
3 bipyramid tetragonal (8) |
6 tetragonal bisphenoid
(4) |
6 pyramid tetragonal (4) |
|
ORTHORHOMBIC POINT GROUPS
|
|
1 rhombic bipyramid (8)
3 rhombic prisms (4)
3 pinacoids (2) |
2 rhombic bisphenoids (4)
3 rhombic prisms (4)
3 pinacoids (2) |
2 rhombic pyramids (4)
4 dihedra (2)
1 rhombic prism (4)
2 pinacoids (2)
2 pedions (1) |
| mmm |
222 |
mm2 |
|
3 rhombic bipyramid (8) |
6 rhombic bisphenoids (4) |
6 rhombic pyramids (4) |
|
Fig.17 - Symmetry and forms constituting the rhomb-cuboctahedron and its dual in
all the subgroups of m3m,
except the ones belonging to the monoclinic and triclinic systems. |
One may note that: - In case of the trigonal point groups,
the polyhedra are orientated with the 3-fold axis set vertically in order to
get a better visualization of the
symmetry of the single forms.
- Concerning the tetragonal point groups, both
4m2 and 42m
subgroups have been reported: they are rotated 45° from each other, with respect to the vertical 4-fold
rotoinversion (or roto-reflection) axis.
The decomposition of the pseudo rhomb-cuboctahedron and its
dual into single forms belonging to point subgroups of
8m2 is shown in
Fig.18.
|
Decomposition of the pseudo rhomb-cuboctahedron and its dual in sets of forms, with lower symmetry, belonging to subgroups
of the 8m2 point group
|
|
2 tetragonal deltohedra
(8)
1 octagonal prism (8)
1 pinacoid (2) |
2 tetragonal deltohedra
(8)
1 octagonal prism (8)
1 pinacoid (2) |
4 tetragonal pyramids (4)
2 tetragonal prisms (4)
2 pedions (1) |
|
8m2 |
8 |
4 |
|
1 octagonal bipyramid (16)
1 tetragonal deltohedron (8) |
3 tetragonal deltohedra
(8) |
6 tetragonal pyramids (4) |
|
2 tetragonal deltohedra
(8)
1 ditetragonal prism (8)
1 pinacoid (2) |
4 rhombic bisphenoids (4)
2 rhombic prisms (4)
1 pinacoid (2) |
4 tetragonal pyramids (4)
2 tetragonal prisms (4)
2 pedions (1) |
4 dihedra (2)
2 rhombic pyramids (4)
1 rhombic prism (4)
2 pinacoids (2)
2 pedions (1) |
|
42*2* |
22*2* |
4mm |
mm2 |
|
2 tetragonal bipyramids
(8)
1 tetragonal deltohedron (8) |
4 rhombic bisphenoids (4)
2 rhombic prisms (4) |
2 ditetragonal pyramids
(8)
2 tetragonal pyramids (4) |
6 rhombic pyramids (4) |
Fig.18 - Symmetry and forms constituting the pseudo rhomb-cuboctahedron
and its dual in all the subgroups of 8m2.
The asterisks in 42*2*
and 22*2* indicates
that the horizontal
2-fold axes are rotated 22.5° with respect to their usual orientation in
422 and 222 cristallographic point groups, in accordance with
their orientation in the 8m2 point group.
Then the (100) faces of the ditetragonal prism, by rotation along the
nearest 2-fold axes, is related to the contiguous (110) and (110)
faces, placed at 45° from (100) face. Hence, geometrically, the prism
is an octagonal prism.
The only subgroups in common between m3m
and 8m2 are:
422, 4mm and 4 (tetragonal system)
222 and mm2 (orthorombic system)
2 and m (monoclinic system)
1 (triclinic system)
The list, relative to the eight shared point subgroups, of the single forms (with
their respective multiplicity) deriving from the decomposition of RCO and pseudo-RCO is
reported in Table 2; the analogous list relative to the decomposition of
their duals is reported in Table 3.
| POINT GROUPS |
RHOMB-CUBOCTAHEDRON
(26 faces) |
PSEUDO RHOMB-CUBOCTAHEDRON
(26 faces) |
| |
|
|
| 422 |
2
tetragonal bipyramids (8) |
2
tetragonal deltohedra (8) |
| |
2
tetragonal prisms (4) |
1
ditetragonal prism (8) |
| |
1
pinacoid (2) |
1
pinacoid (2) |
| |
|
|
| 4mm |
4
tetragonal pyramid (4) |
4
tetragonal pyramids (4) |
| |
2
tetragonal prisms (4) |
2
tetragonal prisms (4) |
| |
2
pedions (1) |
2
pedions (1) |
| |
|
|
| 4 |
4
tetragonal pyramid (4) |
4
tetragonal pyramids (4) |
| |
2
tetragonal prisms (4) |
2
tetragonal prisms (4) |
| |
2
pedions (1) |
2
pedions (1) |
| |
|
|
| 222 |
2
rhombic bisphenoids (4) |
4
rhombic bisphenoids (4) |
| |
3
rhombic prisms (4) |
2
rhombic prisms (4) |
| |
3
pinacoids (2) |
1
pinacoid (2) |
| |
|
|
| mm2 |
2
rhombic pyramids (8) |
4
dihedra (2) |
| |
4
dihedra (2) |
2
rhombic pyramids (4) |
| |
1 prism
(4) |
1
rhombic prism (4) |
| |
2
pinacoids (2) |
2
pinacoids (2) |
| |
2
pedions (1) |
2
pedions (1) |
| |
|
|
| m |
8
dihedra (2) |
8
dihedra (2) |
| |
1
pinacoids (2) |
1
pinacoids (2) |
| |
8
pedions (1) |
8
pedions (1) |
| |
|
|
| 2 |
8
sphenoid (2) |
8
sphenoid (2) |
| |
4
pinacoids (2) |
4
pinacoids (2) |
| |
2
pedions (1) |
2
pedions (1) |
| |
|
|
| 1 |
26
pedions (1) |
26
pedions (1) |
|
Table2 - Decomposition in single forms of the rhomb-cuboctahedron and the pseudo rhombcuboctahedron,
relatively to the shared subgroups of m3m
and 8m2; the multiplicity of each
form, namely the number of its faces, is reported in round brackets. |
| POINT GROUPS |
Dual of the RHOMB-CUBOCTAHEDRON
(24 faces) |
Dual of the PSEUDO RHOMB-CUBOCTAHEDRON
(24 faces) |
| |
|
|
| 422 |
1
tetragonal bipyramid (8) |
2
tetragonal bipyramids (8) |
| |
2
tetragonal trapezohedra (8) |
1
tetragonal deltohedron (8) |
| |
|
|
| 4mm |
2
ditetragonal pyramids (8) |
2
ditetragonal pyramids (8) |
| |
2
tetragonal pyramids (4) |
2
tetragonal pyramids (4) |
| |
|
|
| 4 |
6
tetragonal pyramids (4) |
6
tetragonal pyramids (4) |
| |
|
|
| 222 |
6
rhombic bisphenoids (4) |
4
rhombic bisphenoids (4) |
| |
|
2
rhombic prisms (4) |
| |
|
|
| mm2 |
6
rhombic pyramids (4) |
6
rhombic pyramids (4) |
| |
|
|
| m |
12
dihedra (2) |
11
dihedra (2) |
| |
|
2
pedions(2) |
| |
|
|
| 2 |
12
sphenoids (2) |
12
sphenoids (2) |
| |
|
|
| 1 |
24
pedions (1) |
24
pedions (1) |
|
Table3 - Decomposition in single forms of the duals of
the rhomb-cuboctahedron and the pseudo rhombcuboctahedron, relatively to the
shared subgroups of m3m
and 8m2. |
In particular, concerning the 2 point subgroup, the unique 2-fold axis
is directed along [100] or [110] direction if the subgroup
derives from m3m, whereas it is directed along [100] or
[√2+1 1 0] direction
if the subgroup derives from 8m2.
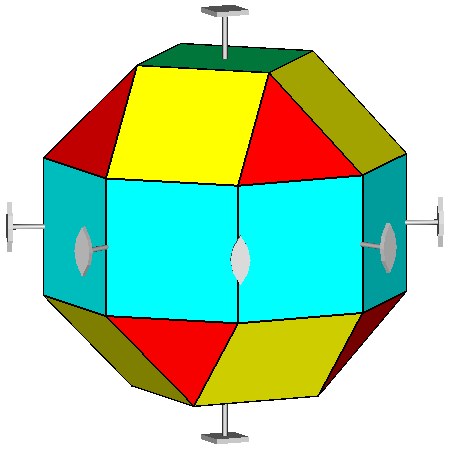
As an example, relatively to the 422 point subgroup, in the next figures one can see RCO, pseudo RCO and their duals,
together with the single forms (all iso-orientated), originating from their decomposition.
|
Symmetry of the rhomb-cuboctahedron in 422 point group
and visualization of the constituting forms |
|
Symmetry of the pseudo
rhomb-cuboctahedron in 422 point group and visualization of the
constituting
forms |
 |
 |
|
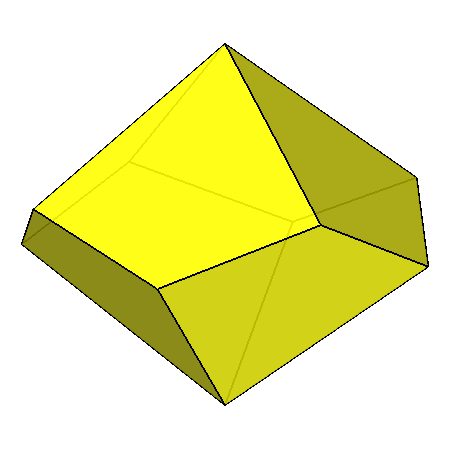 |
|
Fig.20
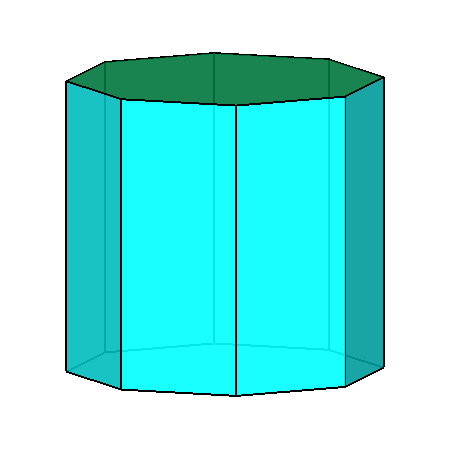
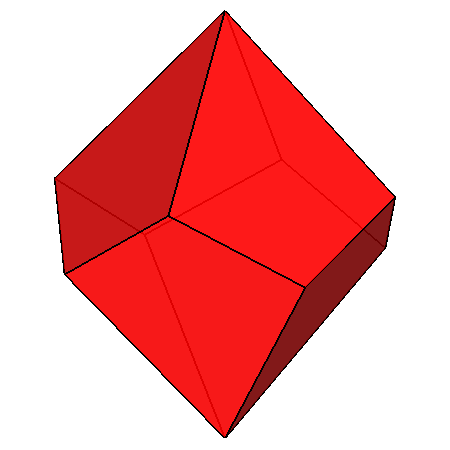
Upper row: pseudo rhomb-cuboctahedron (left)
with the rotation axes relative to the 422 point group; on the right the {110} pale-blue
ditetragonal prism (geometrically corresponding, as already pointed out, to an octagonal prism).
Lower row: {111} red tetragonal deltohedron (left) and {101} yellow tetragonal deltohedron (right)
Also in this case (and in the following ones) the indices have been calculated assuming a monometric set of three orthogonal reference axes.
|
|
Symmetry of the
dual of the rhomb-cuboctahedron in 422 point group and visualization
of the single constituting forms |
|
Symmetry of the dual of the pseudo
rhomb-cuboctahedron in 422 point group and visualization of the single constituting
forms |
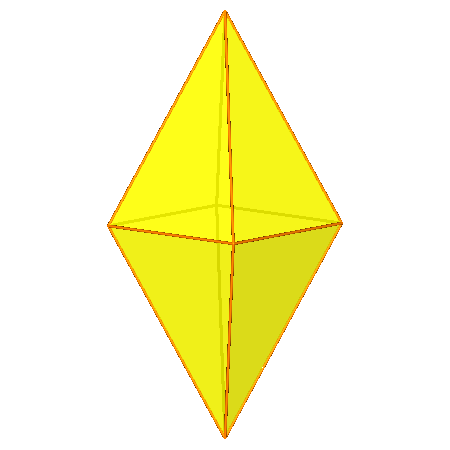
 |
 |

|
 |
|
Fig.22
Upper row: the dual of pseudo rhomb-cuboctahedron with the simmetry axes relative to the 422 point group
(left) and the {1 1 √2+1} violet tetragonal deltohedron
(right).
Lower row: {√2+1 1 1} ochre tetragonal bipyramid (left)
and {1 √2+1 1} yellow tetragonal bipyramid (right).
|
In summary, with regard to the isomeric couple RCO-pseudo RCO evaluated in 422
point group, in addition to the two {110} and {100} tetragonal prisms
transforming into the {100} ditetragonal prism (with octagonal bases),
the {111} and the {101}
tetragonal bipyramids, originating from the decomposition of RCO, become the
corresponding {111}
and {101} tetragonal deltohedra (or isosceles trapezohedra) in case of pseudo-RCO.
Concerning the duals, also the
{1 1 √2+1} tetragonal bipyramid,
originating from the decomposition of the dual of
RCO, becomes the {1 1 √2+1}
tetragonal deltohedron in case of the dual of pseudo-RCO, whereas the {√2+1 1 1}
and {1 √2+1 1}
tetragonal deltohedra, coming from the dual of RCO, become the
{√2+1 1 1}
and {1 √2+1 1}
tetragonal bipyramids in case of the dual of pseudo-RCO.
ACKNOWLEDGEMENTS
Many thanks are due to Riccardo Basso for the fruitful discussions and to
Fabio Somenzi for his precious help concerning the translation of the text.
REFERENCES and LINKS
1) J. Kepler
De nive sexangula, Prague, 1611
2) C. Hardie
The Six-cornered Snowflake, Oxford University Press, 1966
3)
Peter R. Cromwell
Polyhedra,
Cambridge University Press, 1997
4)
W.W. Rouse Ball, H.S.M. Coxeter
Mathematical Recreations and Essays, Dover Publications,
1987
5)
http://www.georgehart.com/virtual-polyhedra/pseudo-rhombicuboctahedra.html
6) Norman W. Johnson
Convex Polyhedra with Regular Faces, Canadian Journal of Mathematics,
18, 169-200, 1966
7) Viktor A. Zalgaller
Convex Polyhedra with Regular Faces, Seminars in Mathematics - V.A.
Steklov Mathematical Institute, Leningrad - Volume 2, Consultants Bureau, 1969











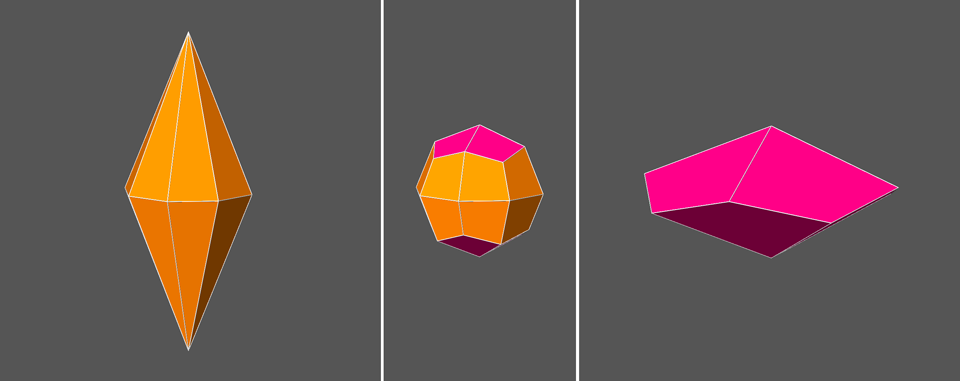


_RCO_m3m__s.png)
_RCO_432__s.png)
_RCO_m(B3)__s.png)
_RCO_(B4)3m__s.png)
_RCO_23__s.png)
_dual_RCO_m3m__s.png)
_dual_RCO_432__s.png)
_dual_RCO_m(B3)__s.png)
_dual_RCO_(B4)3m__s.png)
_dual_RCO_23__s.png)
_RCO_(B3)2_over_m__3fold_axis_111_vert_clino__s.png)
_RCO_B3__s.png)
_RCO_32__3fold_axis_111_vert_clino__s.png)
_RCO_3m__s.png)
_RCO_3__s.png)
m__s.png)
_RCO_(4over_m)_mm__s.png)
_RCO_422__s.png)
_RCO_(B4)m2__s.png)
_RCO_(B4)2m__s.png)
_dual_RCO_(4over_m)_mm__s.png)
_dual_RCO_422__s.png)
_dual_RCO_(B4)m2__s.png)
_dual_RCO_(B4)2m__s.png)
_RCO_4mm__s.png)
_RCO_(4over_m)__s.png)
_RCO_(B4)__s.png)
_RCO_4__s.png)
_dual_RCO_4mm__s.png)
_dual_RCO_4over_m__s.png)
_dual_RCO_B4__s.png)
_dual_RCO_4__s.png)
_RCO_mmm__s.png)
_RCO_222__s.png)
_RCO_mm2__s.png)
_dual_RCO_mmm__s.png)
_dual_RCO_222__s.png)
_dual_RCO_mm2__s.png)
m2__225px.png)
m2_.png)