 |
|
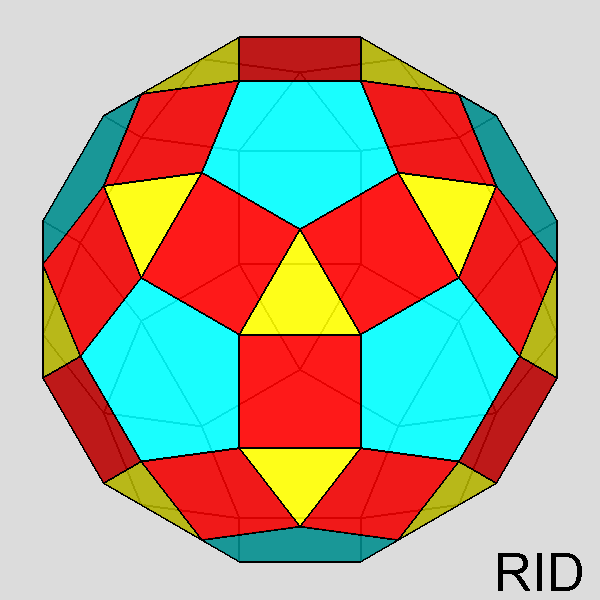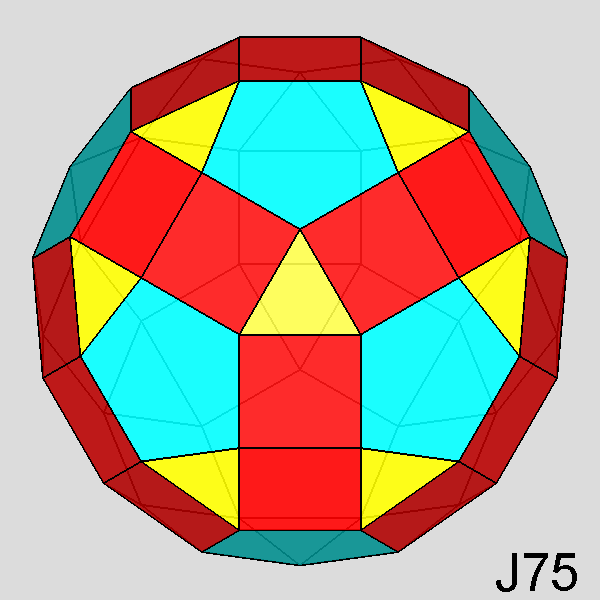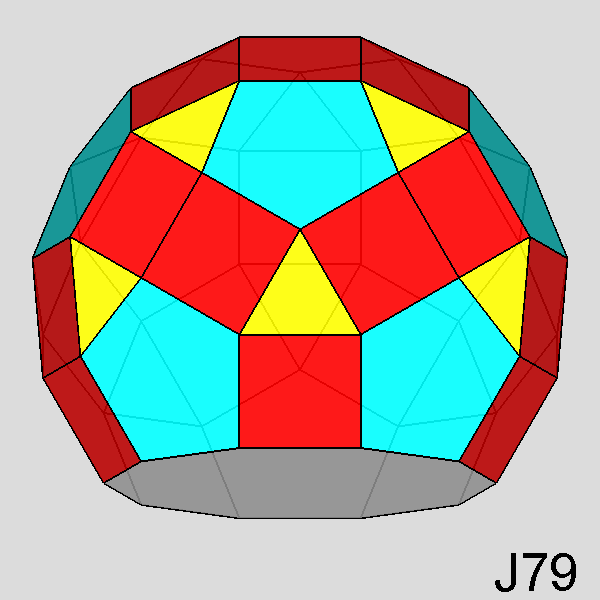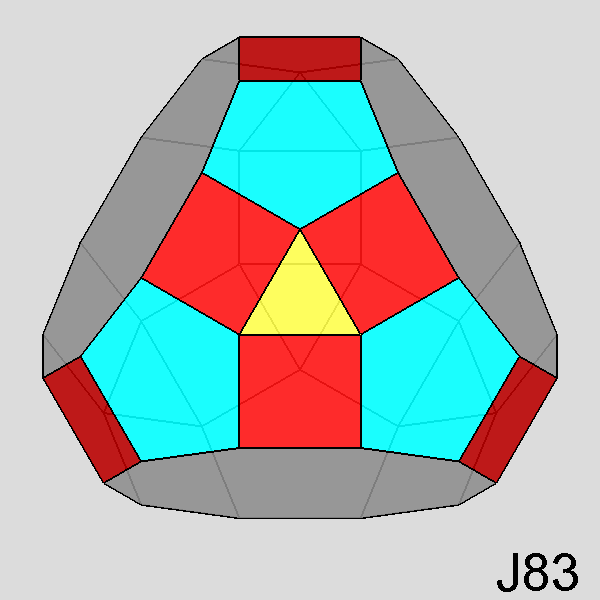
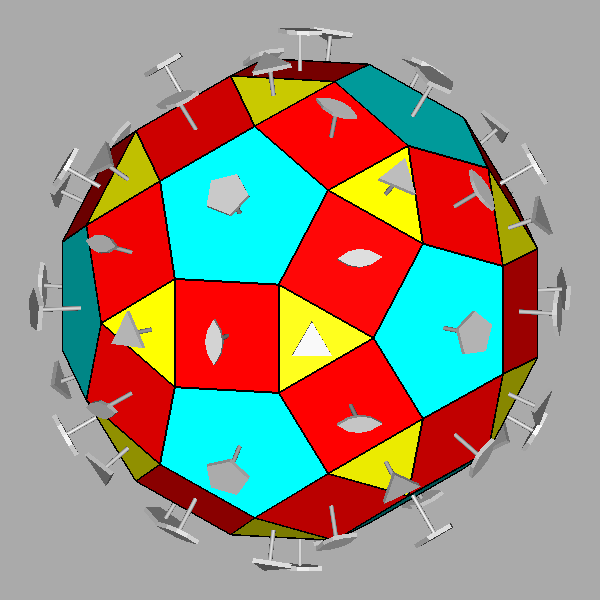
Animation showing the rhomb-icosidodecahedron and the derived Johnson's polyhedra obtained by the rotation and/or removal of the pentagonal cupolas. |
Dissection of the rhomb-icosidodecahedron in elementary regular-faced polyhedra and subsequent reassembly leading to a set of Johnson's polyhedra
Livio Zefiro
Dip.Te.Ris, Universita' di Genova, Italy
(E-mail address: livio.zefiro@fastwebnet.it)
Notes
|
 |
|
Animation showing the rhomb-icosidodecahedron and the derived Johnson's polyhedra obtained by the rotation and/or removal of the pentagonal cupolas. |
|
 |
|
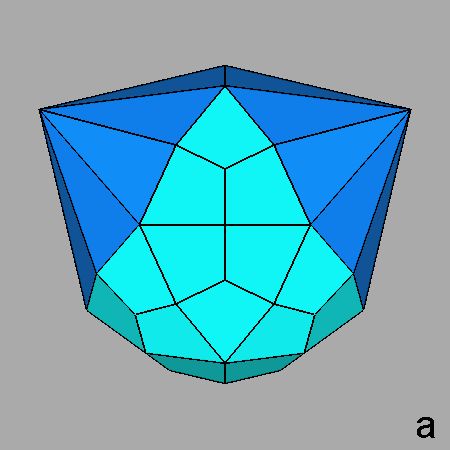
Fig. 2
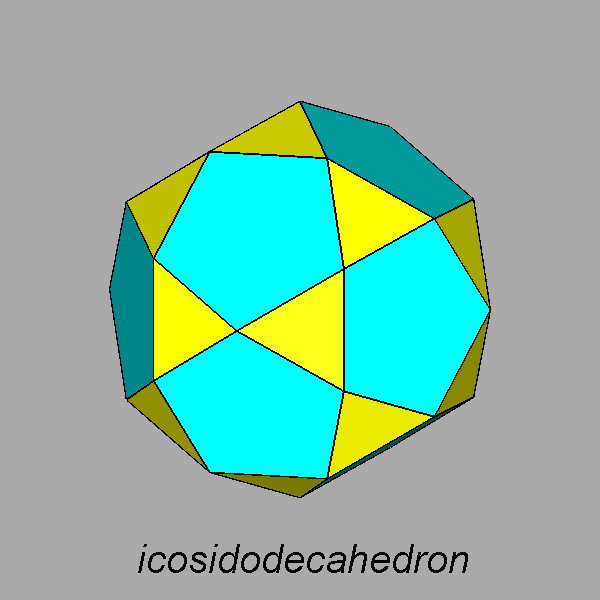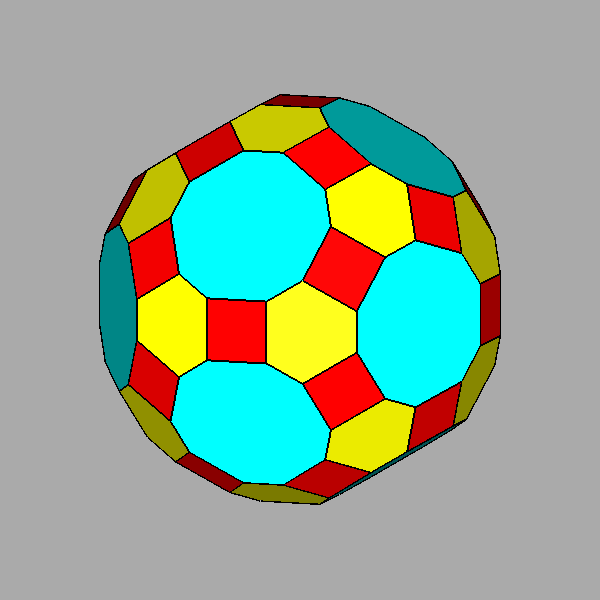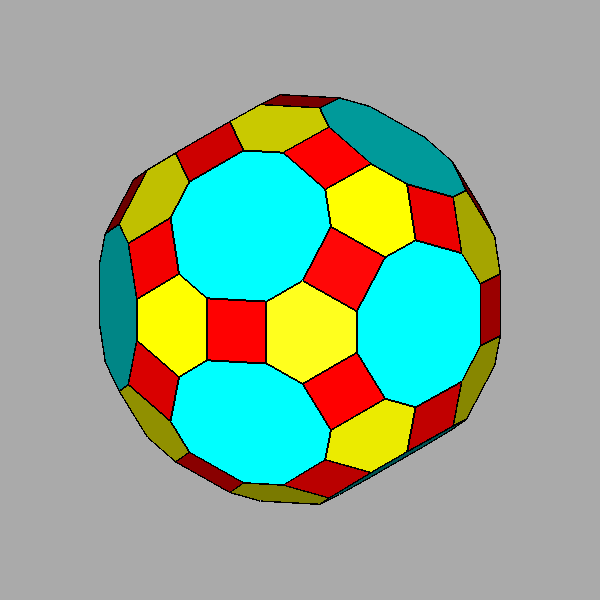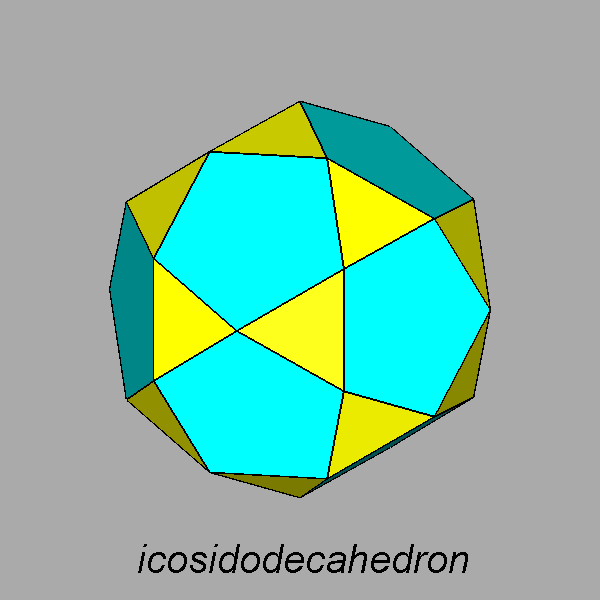
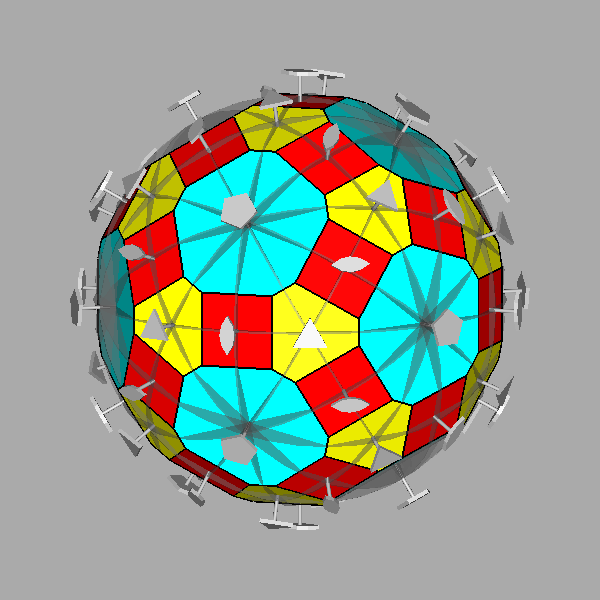
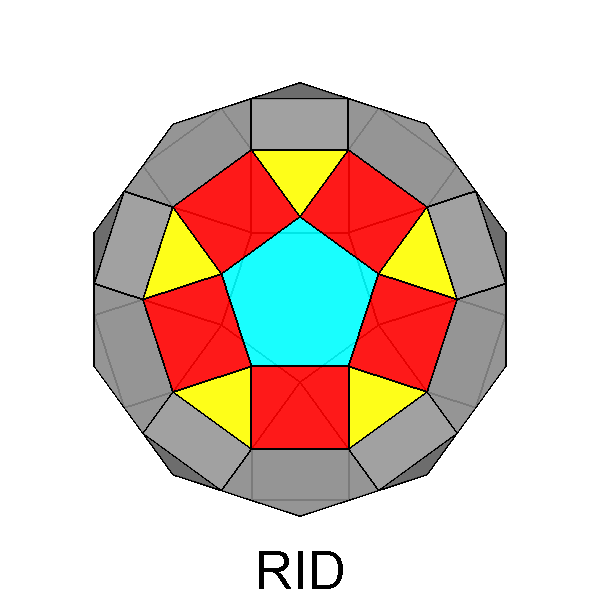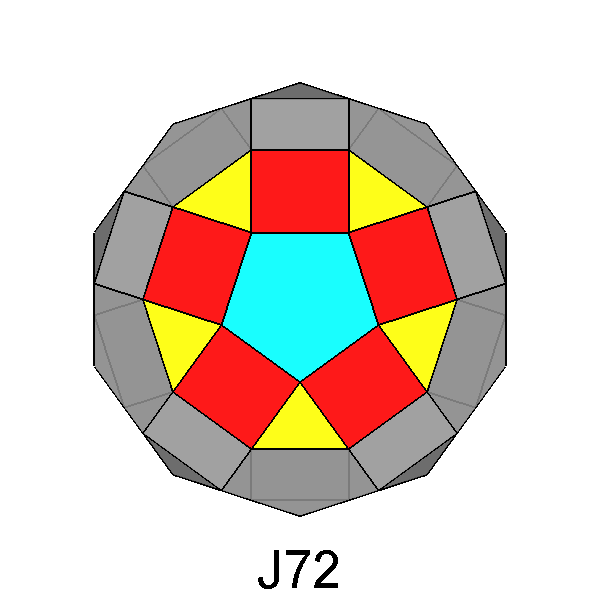
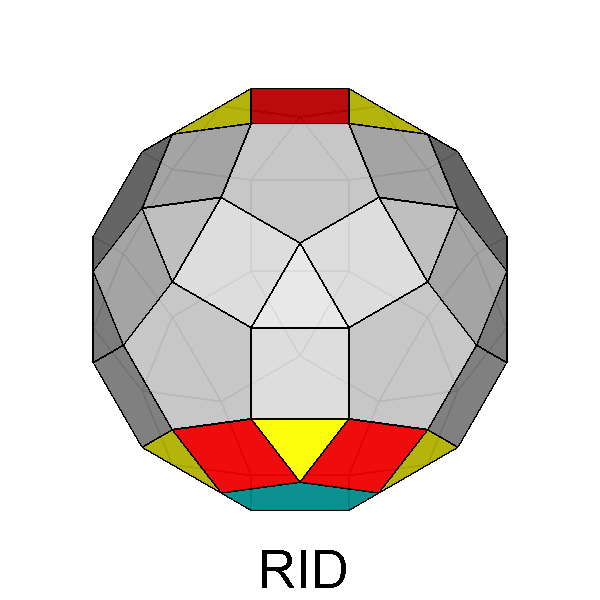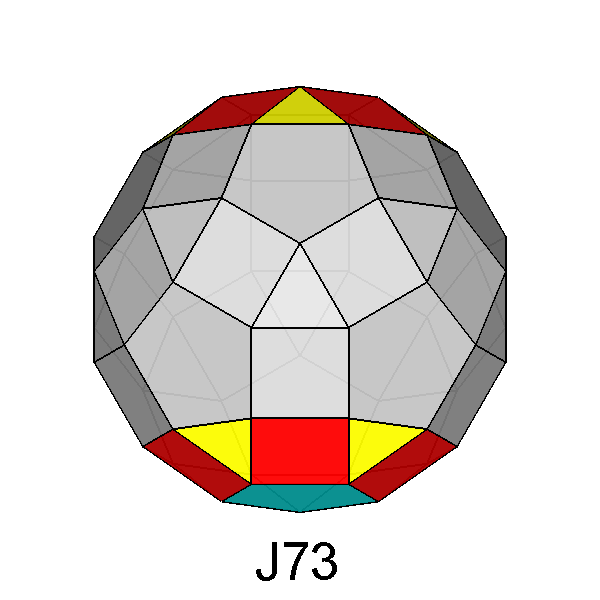
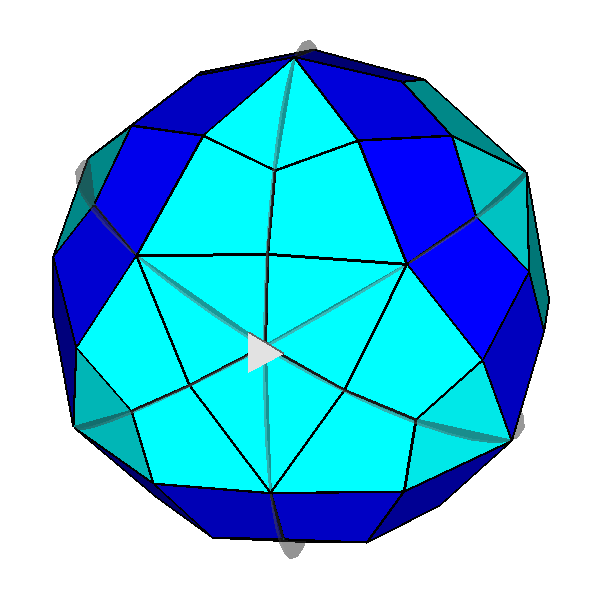
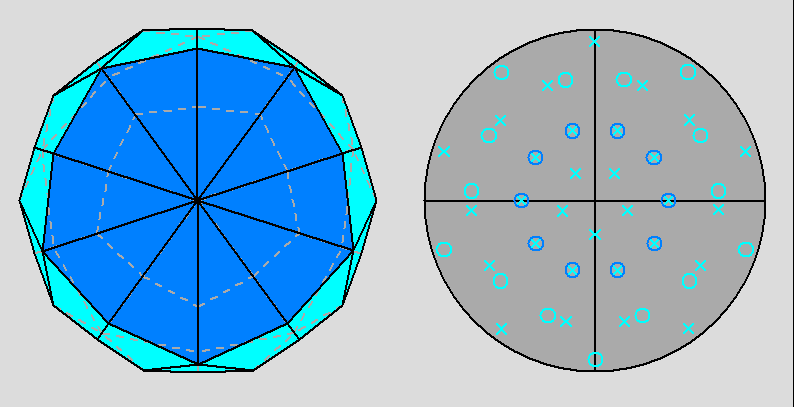
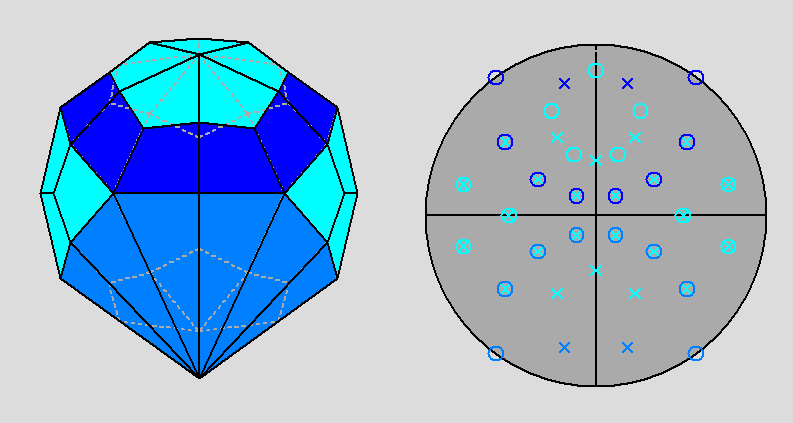
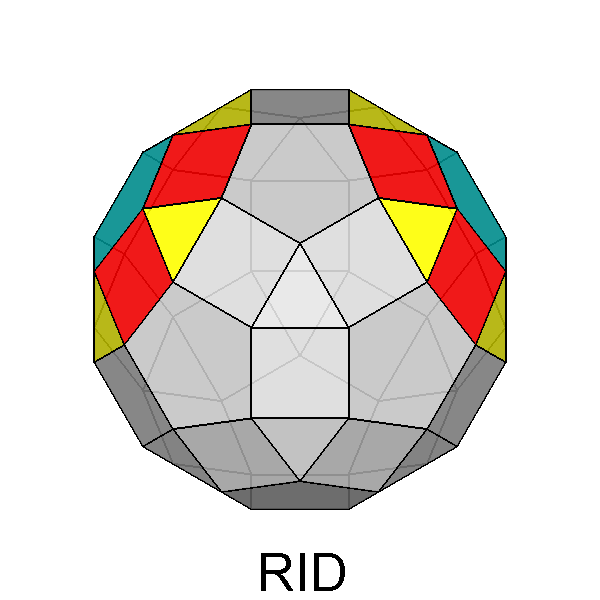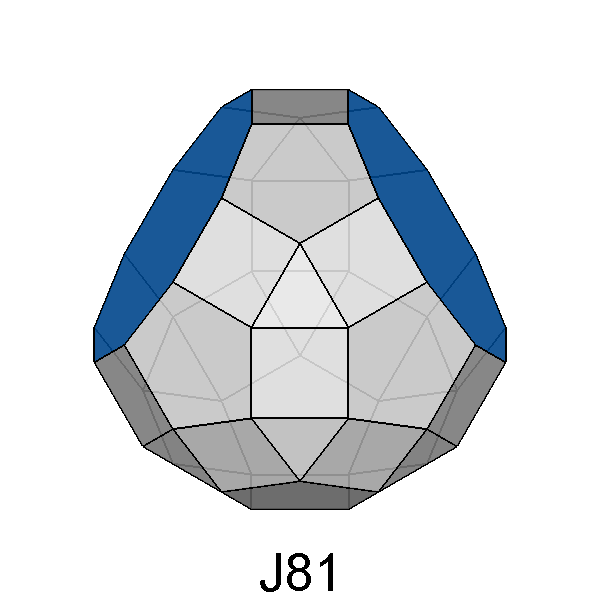
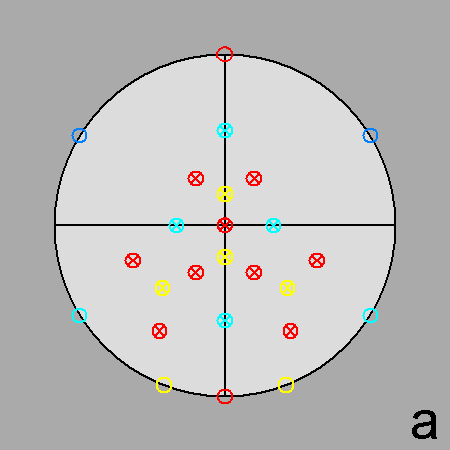
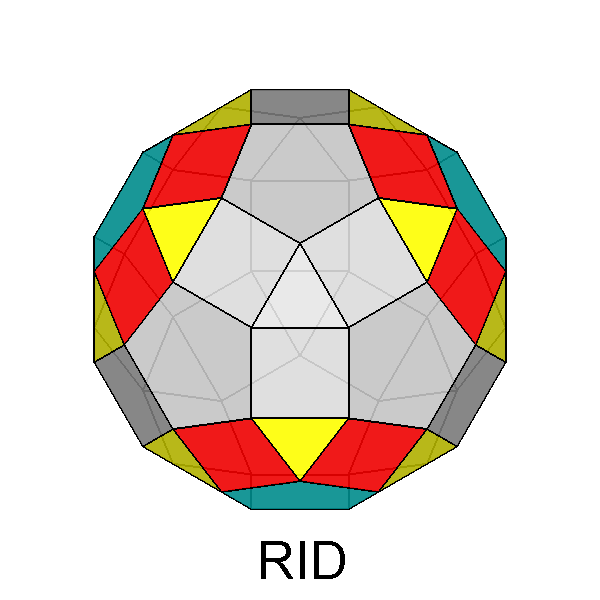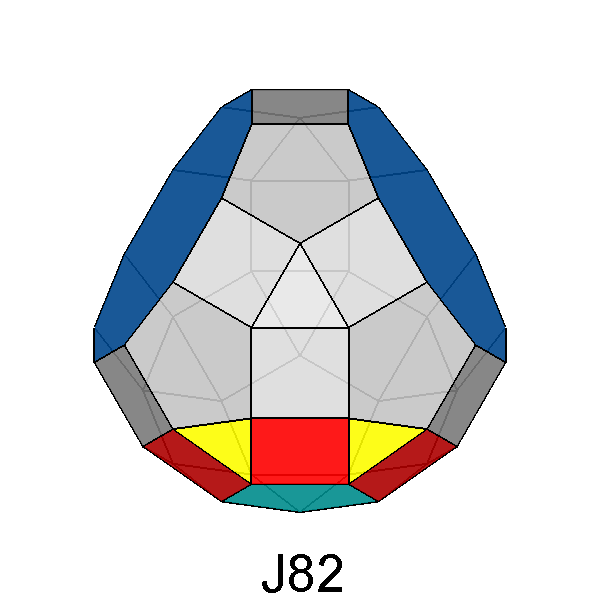
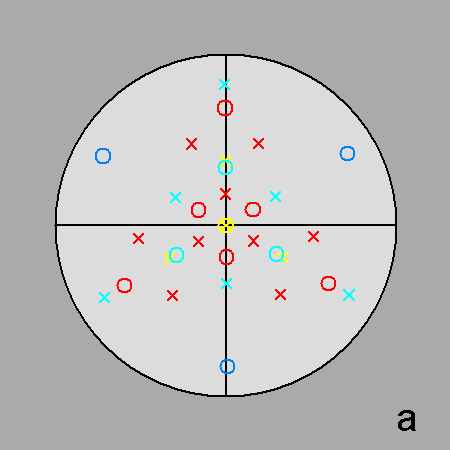
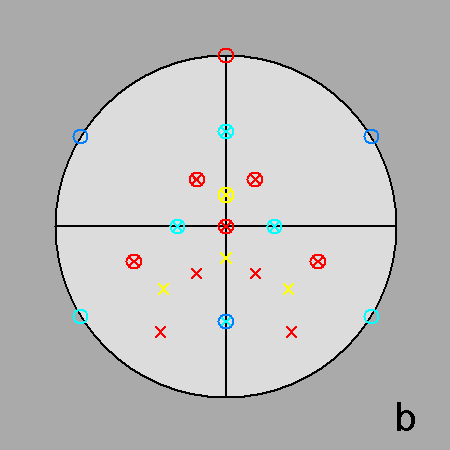
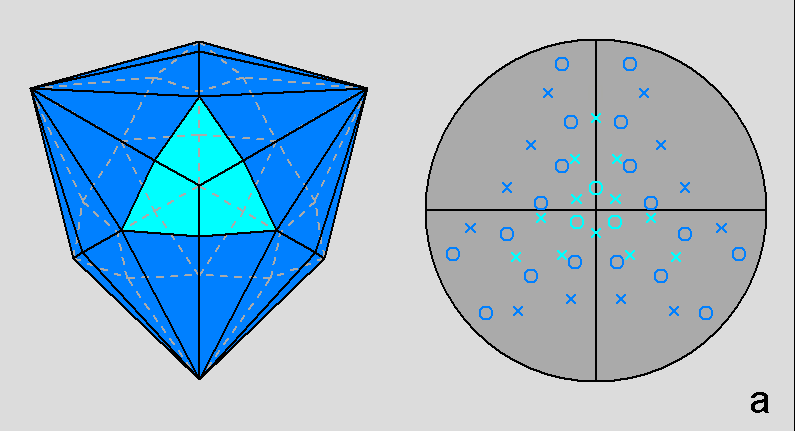
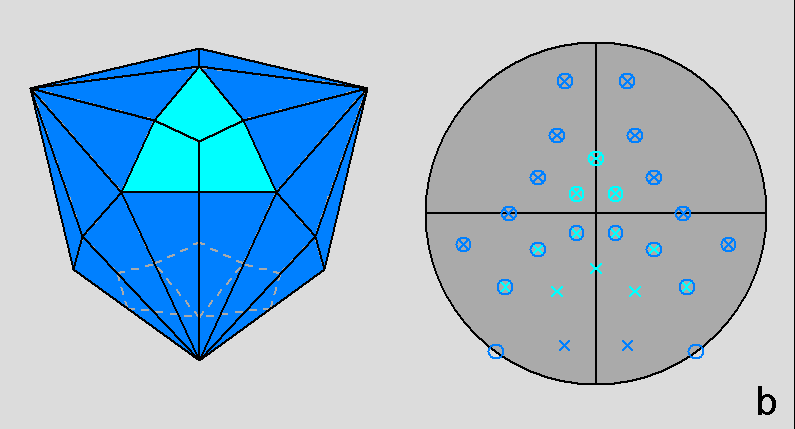
The Archimedean rhomb-icosidodecahedron with the 2-fold, 3-fold
and 5-fold rotation axes characterizing the 235 point group. |
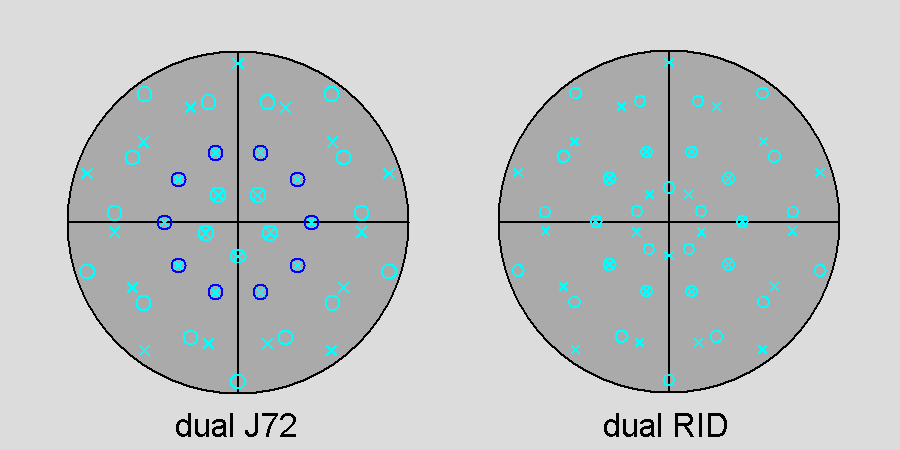
The stereographic projections of the rhomb-icosidodecahedron viewed along
the 2-fold, 3-fold and 5-fold axes are sequentially reported in Figure 3
(the small circles and the x-shaped characters represent normals to the faces directed
upwards or downwards, respectively).
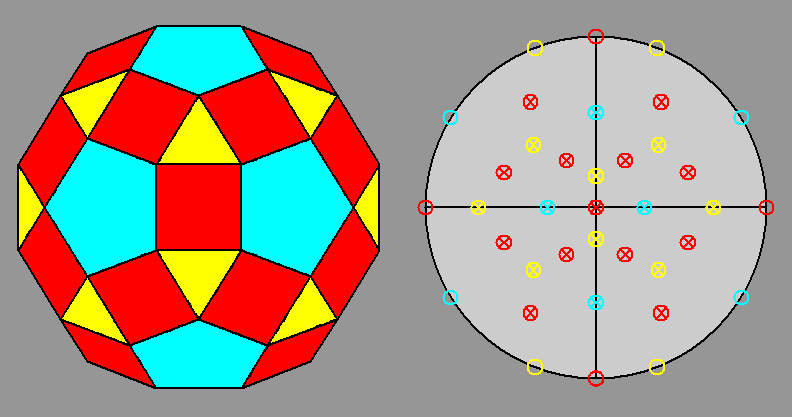 |
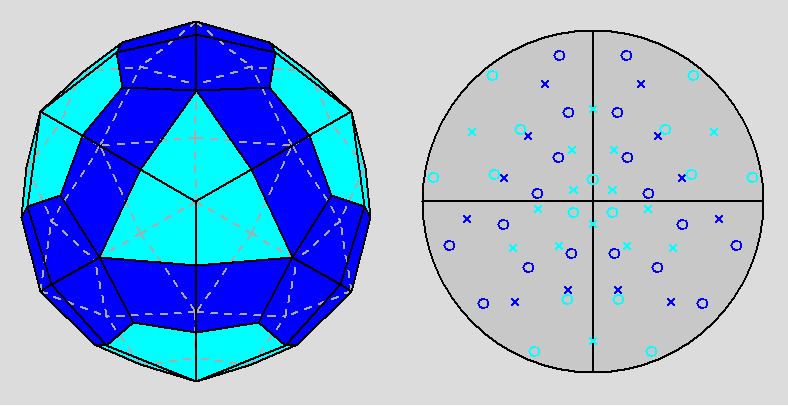
| Fig. 3a - The rhomb-icosidodecahedron and its stereographic projection along a 2-fold rotation axis. |
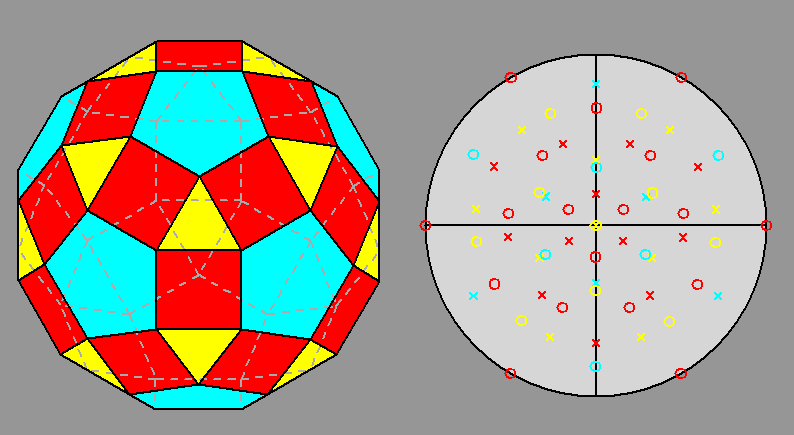 |
| Fig. 3b - The rhomb-icosidodecahedron and its stereographic projection along a 3-fold rotation axis. |
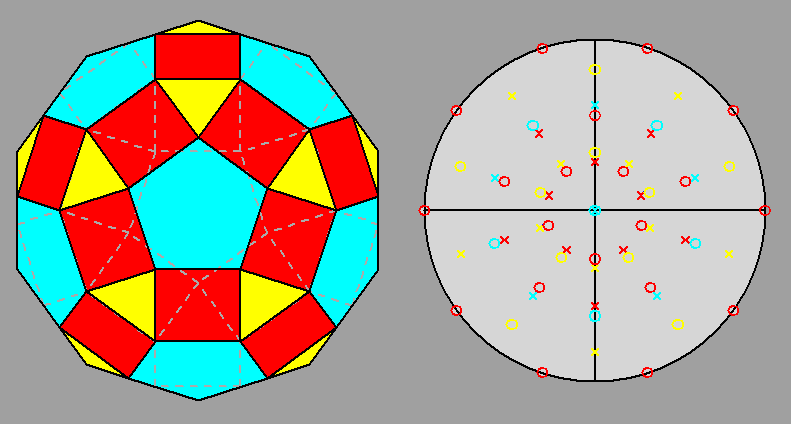 |
| Fig. 3c - The rhomb-icosidodecahedron and its stereographic projection along a 5-fold rotation axis. |
As already shown in [4], even if it is not possible to obtain the rhomb-icosidodecahedron by the direct truncation of an icosi-dodecahedron, the two polyhedra share the relationship:
between the distances, from the centre of each polyhedron, of their
icosahedral and dodecahedral faces, given a unit value to the central distance
of the rhomb-triacontahedral faces.
The relationship holds true, in the intervals:
 |
|
Fig. 4 - Transition from the icosidodecahedron to the rhomb-icosidodecahedron,
through the Archimedean truncated icosi-dodecahedron: the red triacontahedral
faces,
tangent to the vertices and therefore absent in the icosidodecahedron, are square in all the intermediate polyhedra.
|
 |
|
Fig. 5 - Mirror planes and rotation axes which characterize a
generic non-Archimedean polyhedron belonging to the series of polyhedra intermediate
between the icosi-dodecahedron and the rhomb-icosidodecahedron:
|
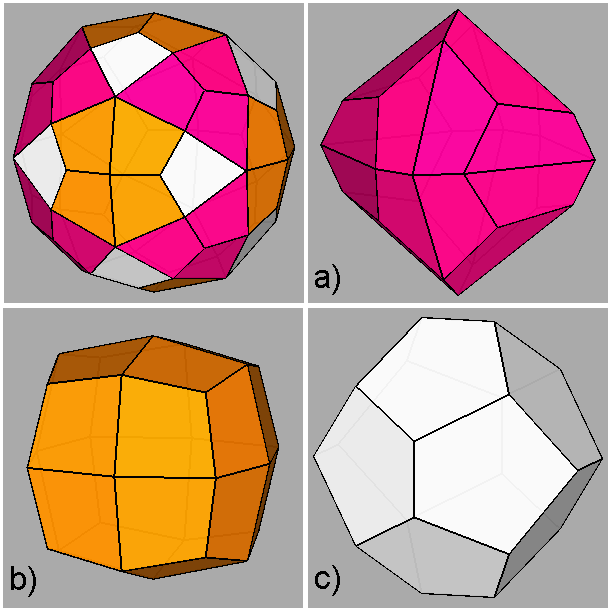
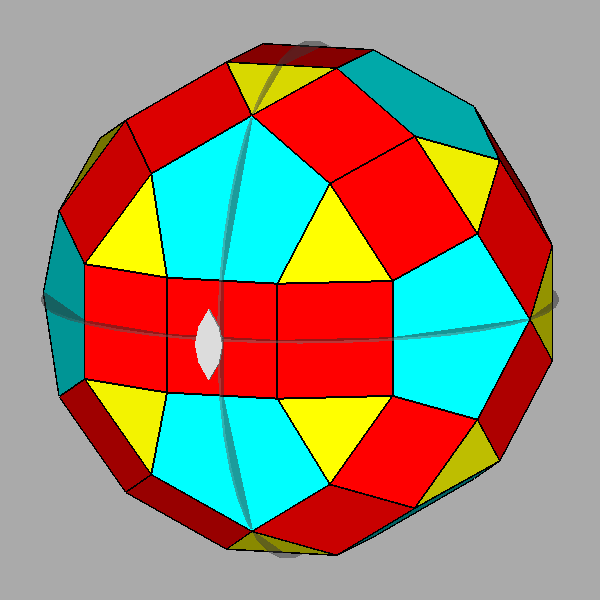
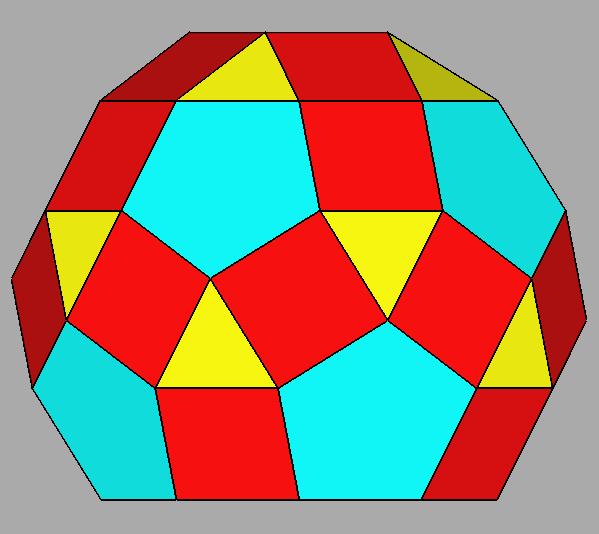
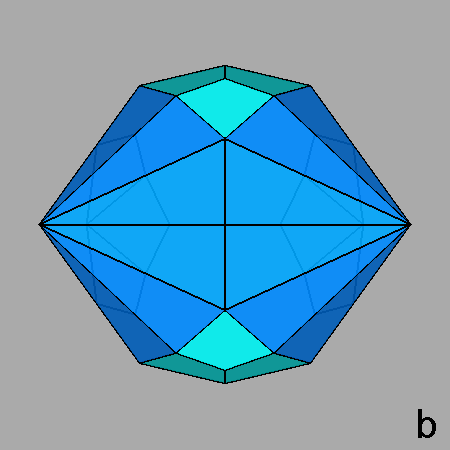
The polyhedron dual [5] of the Archimedean rhomb-icosidodecahedron is the Catalan deltoidal hexecontahedron shown in Figure 6, whose faces are identified by indices deriving from the cyclic permutations, changes of sign included, of the following Miller indices:
 |
|
Fig. 6 Clinographic view of the Catalan deltoidal hexecontahedron,
dual of the Archimedean rhomb-icosidodecahedron, showing the positioning of the fifteen 2-fold, the ten |
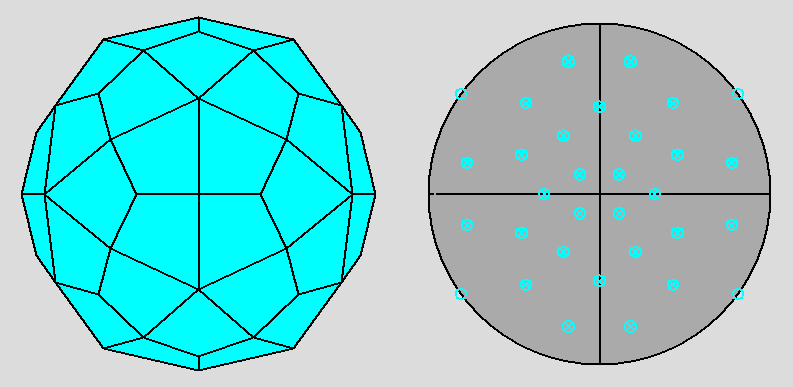 |
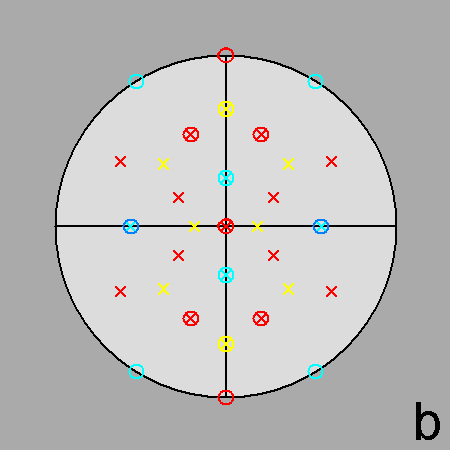
Fig. 7a - The deltoidal hexecontahedron, dual of the rhomb-icosidodecahedron, and its stereographic projection
viewed along a 2-fold rotation axis (to be compared with
Fig. 3a). |
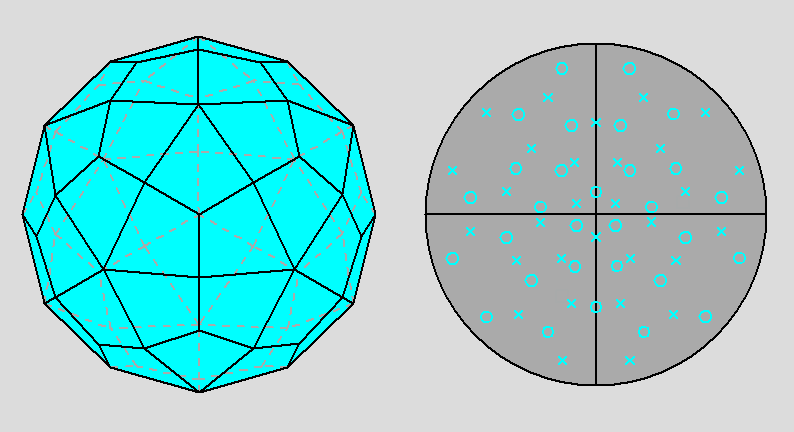 |
Fig. 7b - Deltoidal hexecontahedron, dual of the
rhomb-icosidodecahedron, and its stereographic projection viewed along a 3-fold rotation axis
(to be compared with
Fig. 3b). |
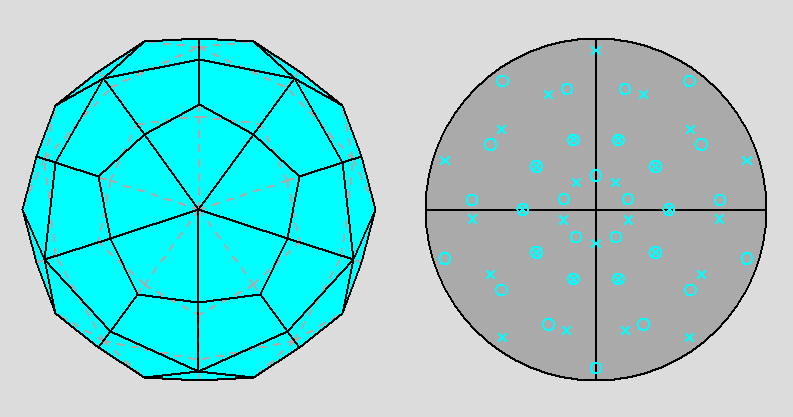 |
Fig. 7c - The deltoidal hexecontahedron, dual of the
rhomb-icosidodecahedron, and its stereographic projection viewed along a 5-fold rotation axis (to be compared with
Fig. 3c). |
 |
|
Fig. 8
Decomposition of the Catalan deltoidal hexecontahedron in three single forms
belonging to the m3 point group:
a) {2 1 τ} diploid (or diakisdodecahedron)
b) {τ2 1/τ 1/τ} deltoidal icositetrahedron c) {τ+1/τ τ 0} pentagon-dodecahedron |
 |
|
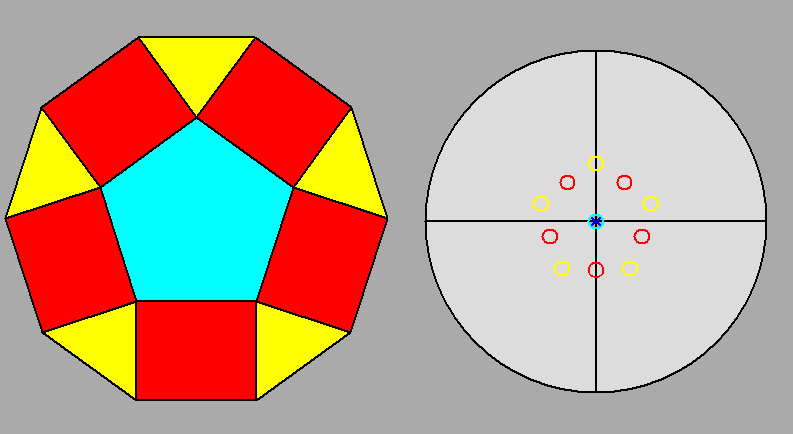
Fig. 9 - Projection of a pentagonal cupola along the normal to the pentagonal face and the relative stereographic net.
The angles between the normal to the pentagonal face and each normal to the square and triangular faces measure 31.72° and 37.38°, respectively. |
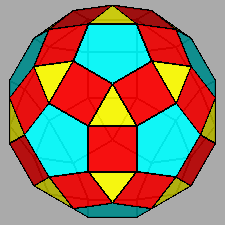
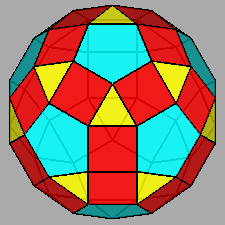
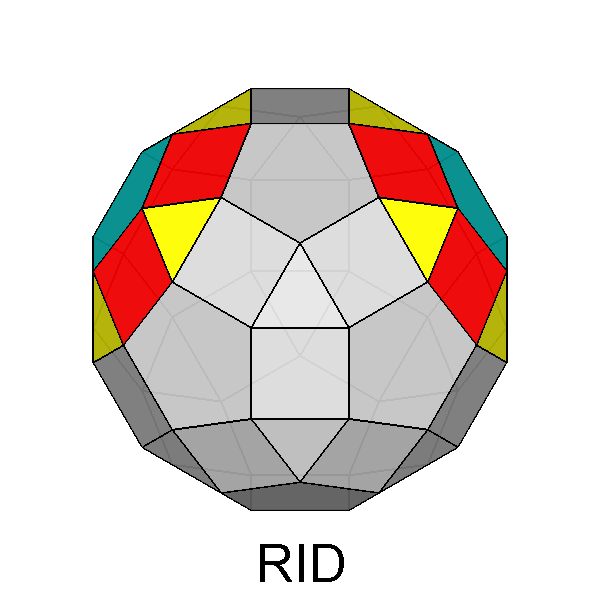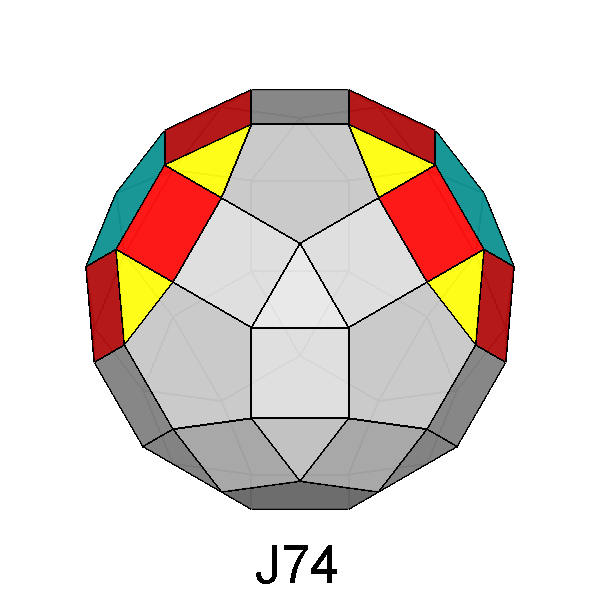
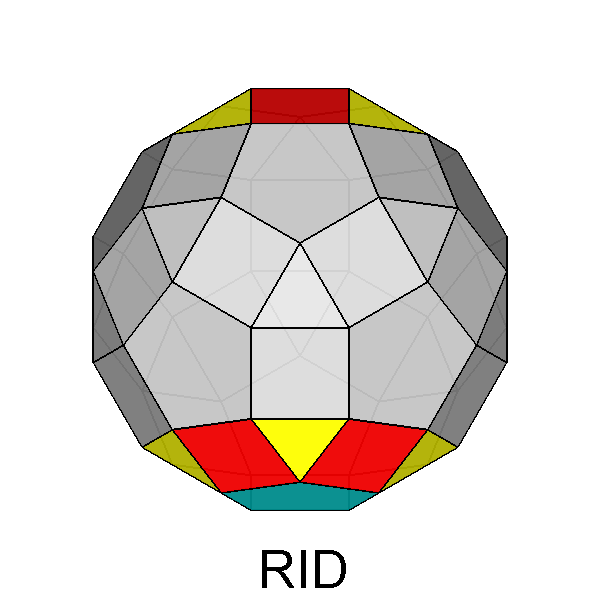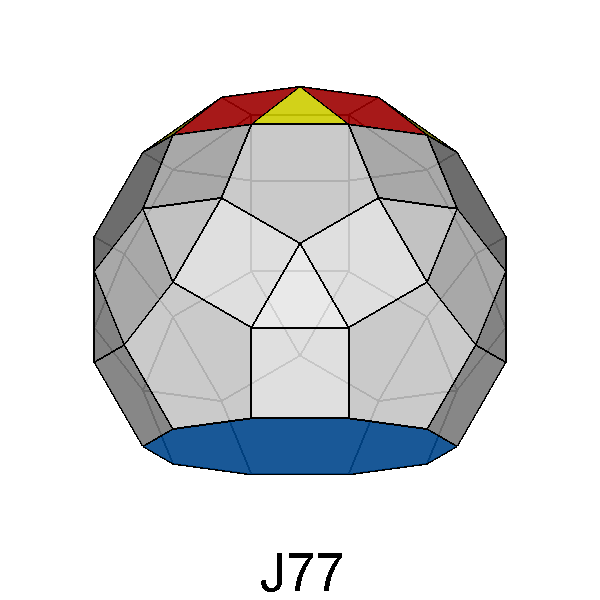
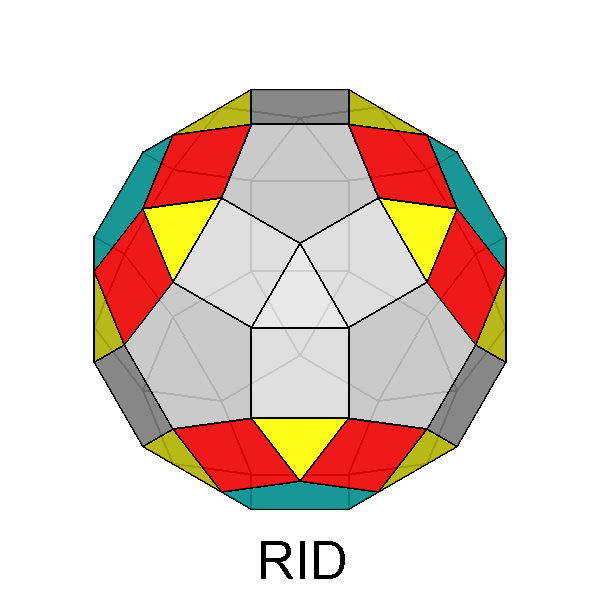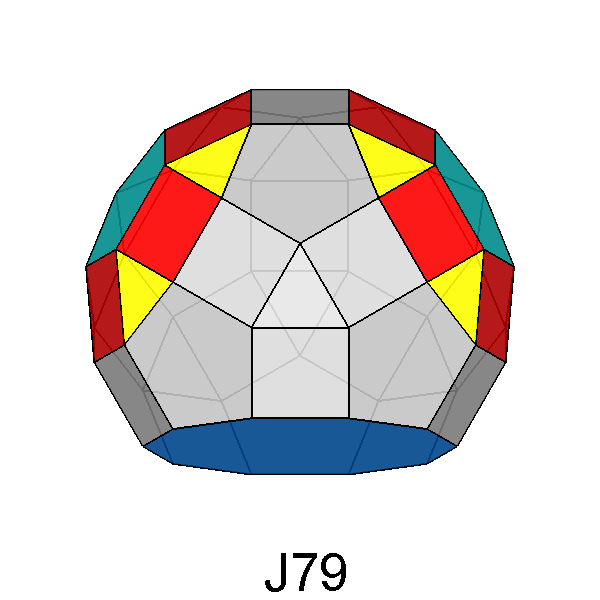
| FIG. 10a | |||
 |
 |
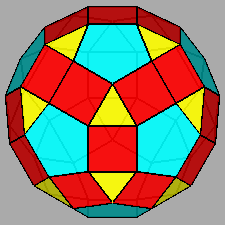 |
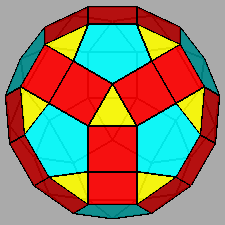 |
|
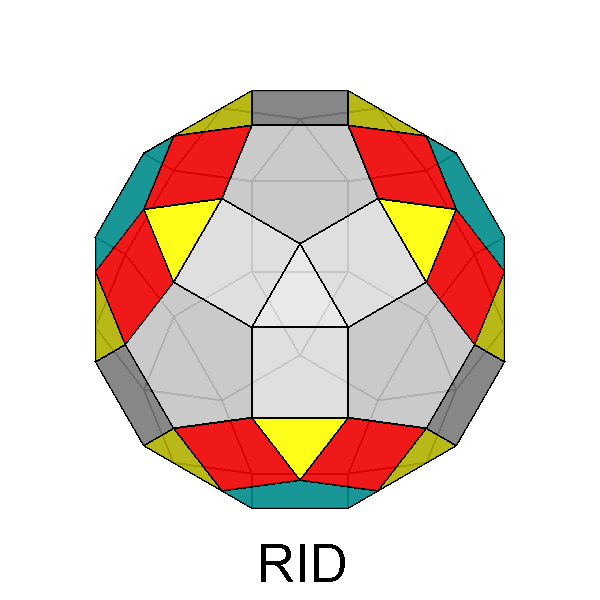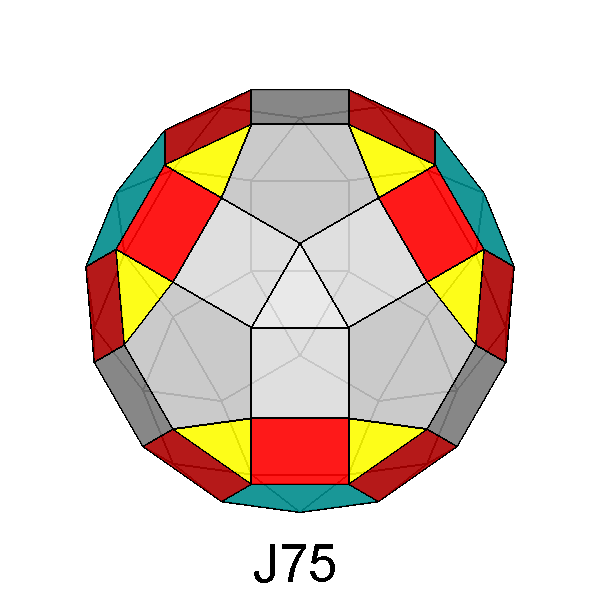
Gyrate RID (J72) |
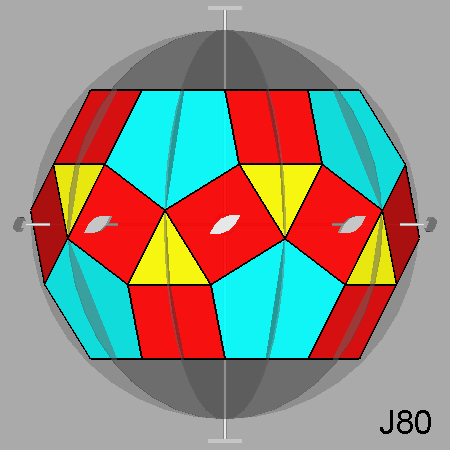
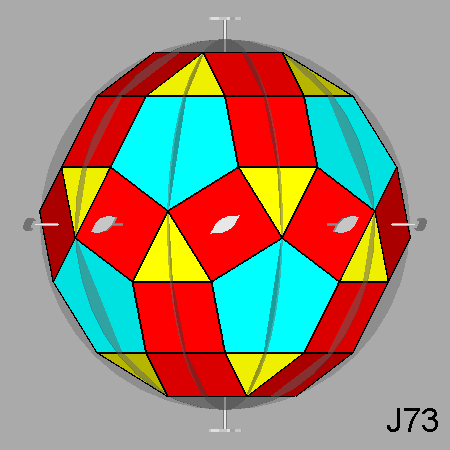
Parabigyrate RID (J73) |
Metabigyrate RID (J74) |
Trigyrate RID (J75) |
| FIG. 10b | |||
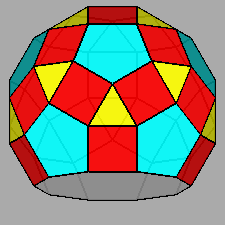 |
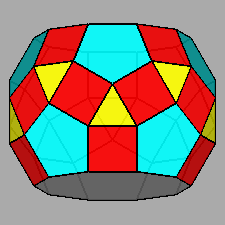 |
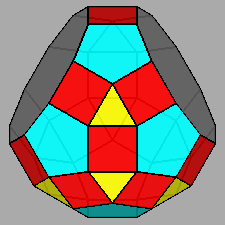 |
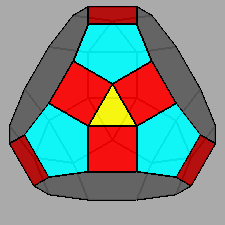 |
|
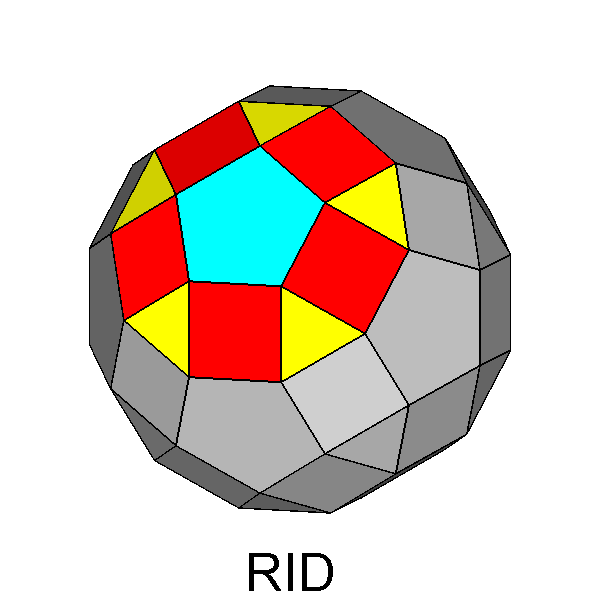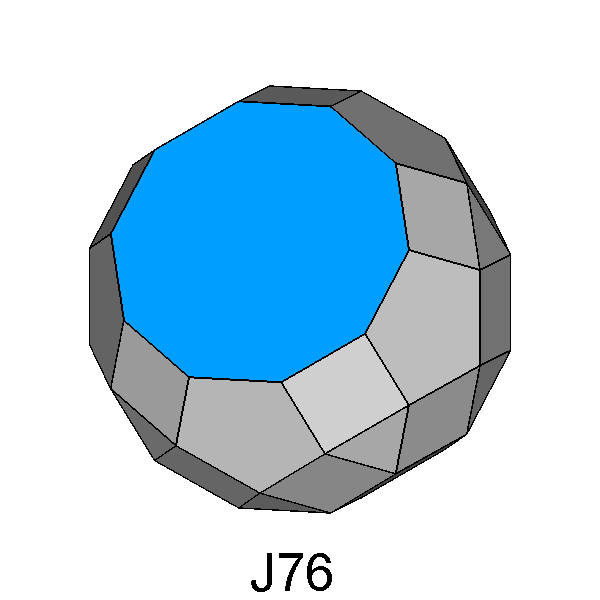
Diminished RID (J76) |
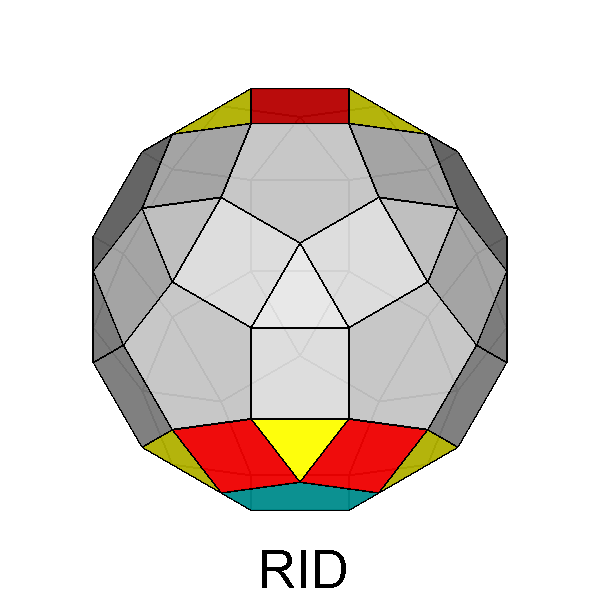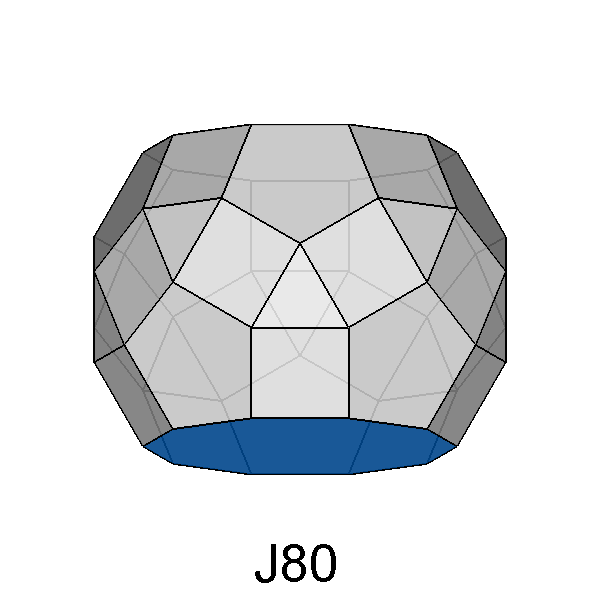
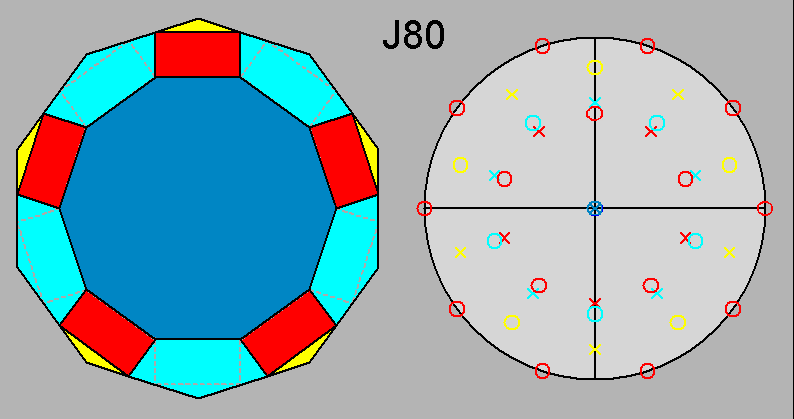
Parabidiminished RID (J80) |
Metabidiminished RID (J81) |
Tridiminished RID (J83) |
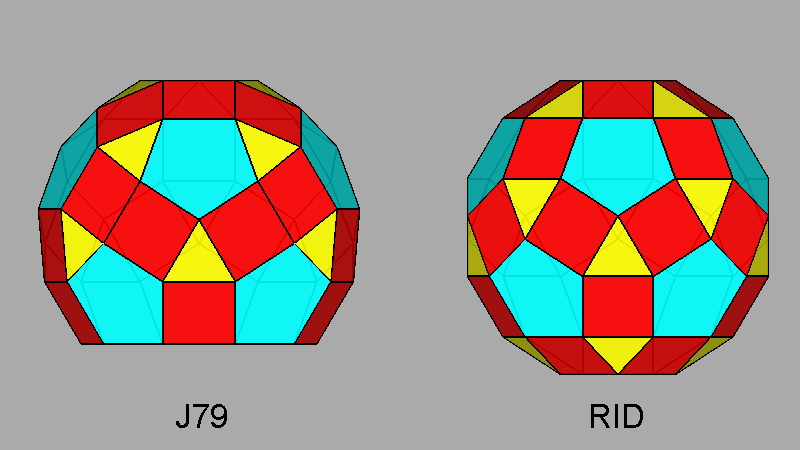
| FIG. 10c | |||
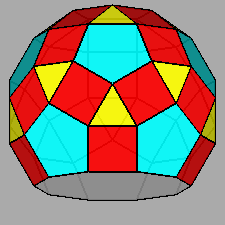 |
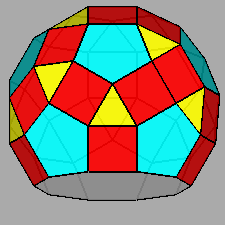 |
 |
 |
|
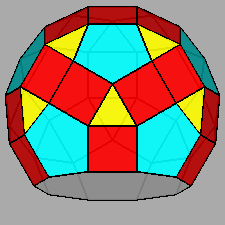
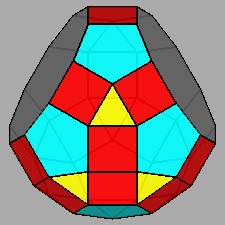
Paragyrate diminished RID (J77) |
Metagyrate diminished RID (J78) |
Bigyrate diminished RID (J79) |
Gyrate bidiminished RID (J82) |
In addition to the previous twelve Johnson's polyhedra, the thirteenth
one deriving from the RID is the pentagonal cupola itself.
 |
|
Fig. 11 - Animation showing the derivation of the gyrate RID
from the RID by a 180° rotation of the highlighted pentagonal cupola. Both polyhedra are viewed along
a direction corresponding to
a 5-fold axis. |
 |
|
Fig. 12 - Clinographic view of the gyrate RID, showing
the five mirror planes and the 5-fold axis. |
The gyrate RID viewed along the 5-fold axis and the corresponding stereographic
net are shown in Figure 13; the indices of the faces of the rotated
cupola in J72, compared with the indices of the faces of the corresponding
cupola in the RID, are reported in the Appendix A.
 |
|
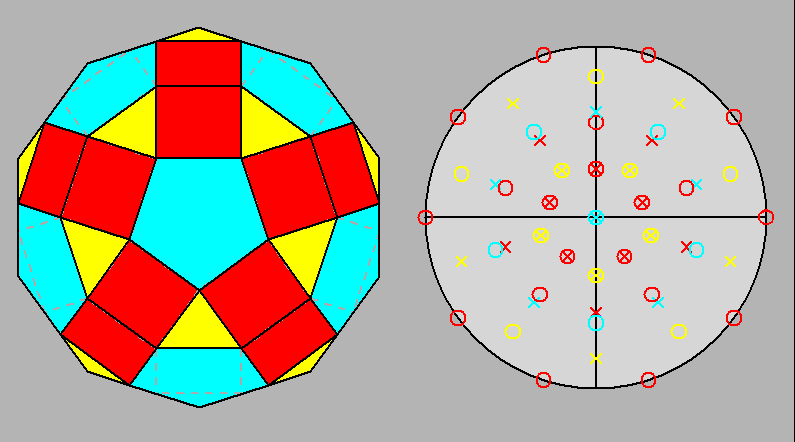
Fig. 13
Projection of the gyrate RID (J72) along its 5-fold axis and the relative stereographic net
(to be compared with Fig. 3c). Only the faces of the rotated pentagonal cupola are exactly superimposed to the corresponding faces of the opposite pentagonal cupola which has not been rotated. |
 |
 |
|
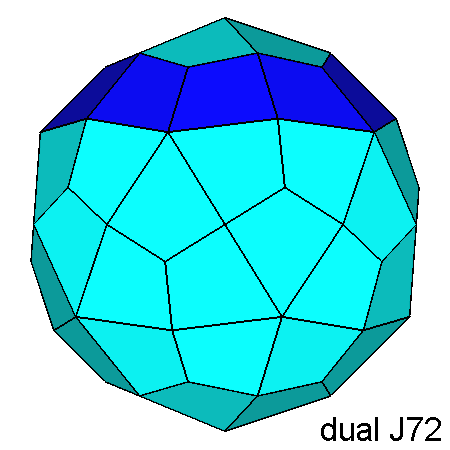
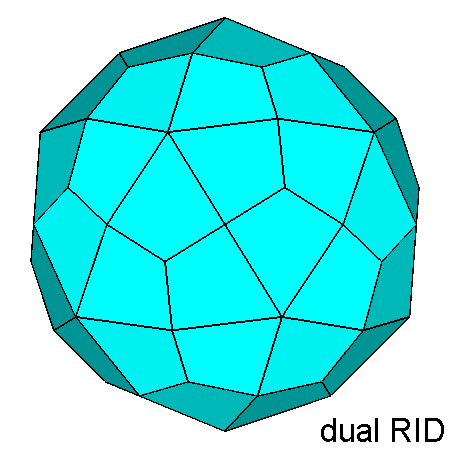
Fig. 14 - The polyhedron dual of the gyrate RID (on the left), projected along
the direction [010]
and compared with the dual of the RID (on the right). | |
The ten dark-blue faces of the dual of the gyrate RID have
a four-sided shape, different from the other fifty faces (in pale blue),
which are kite-shaped just like all the faces of the Catalan deltoidal hexecontahedron, dual
of the RID.
As one can see in Figure 15 from the views, along the [τ
01] direction, of the duals of both RID and gyrate RID, the
changes between the two polyhedra involve fifteen faces:
whereas the ten dark-blue faces have a different four-sided shape but an equal orientation in respect to the
corresponding kite-shaped faces of the dual of the RID, the five faces nearest to the 5-fold axis, and
contiguous to the dark-blue faces, have the same shape (and pale-blue
color) of the faces of the
dual of the RID but they are rotated of 180° around the 5-fold axis.
 |
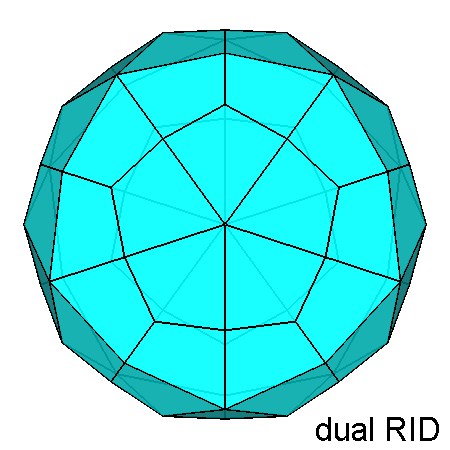 |
Fig. 15
Comparison between the dual of the gyrate RID (on the left)
and the dual of the RID (on the right),
projected along the [τ 01] direction. The ten faces in dark-blue, making a ring, have a generic four-sided shape: they differ from the other fifty kite-shaped faces, in pale-blue, of the dual of the gyrate RID, equal to the faces of the dual of the RID. Moreover in the gyrate RID the five kite-shaped faces inside the ring of ten dark-blue faces are 180° rotated relatively to the corresponding five faces of the dual of the RID. | |
 |
|
Fig. 16
Comparison between the stereographic projections of the
duals of gyrate RID (left)
and RID (right) along the
[τ 01] pentagonal axis. As a consequence of the 180° rotation in J72 of the fifteen vertices of the 5-fold cupola, the faces of the dual of J72 corresponding to such rotated vertices undergo an equal rotation so that, analogously to the faces belonging to the two 10-fold pyramids, also the faces of the rotated |
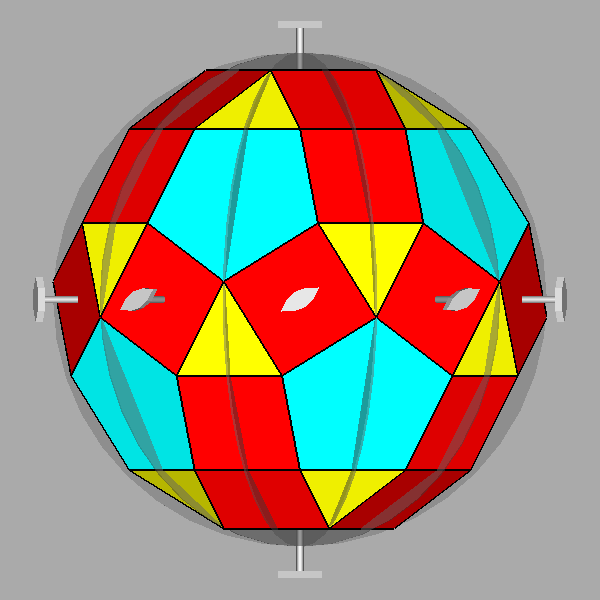
Parabigyrate rhomb-icosidodecahedron (J73)
 |
|
Fig. 17 - Parabigyrate RID obtained by a 180° rotation of the
highlighted pentagonal cupolas of a RID. |
 |
|
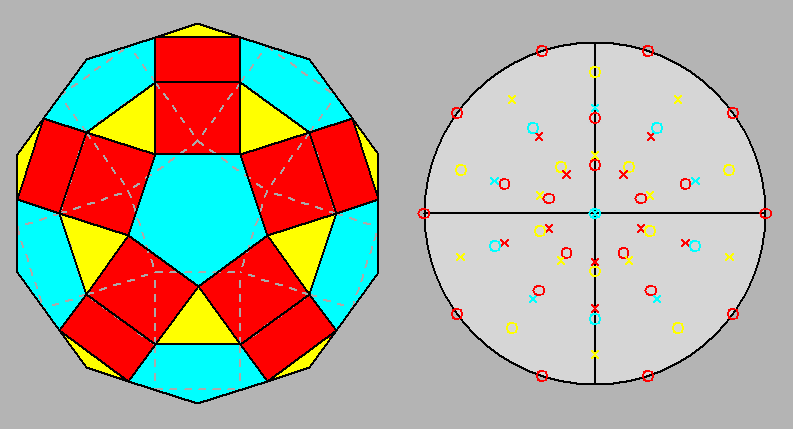
Fig. 18 - View of the parabigyrate RID along the
[010]
direction, showing the five 2-fold axes: each of them is normal to both the
5-fold axis and a mirror plane. |
 |
|
Fig. 19
Projection of the parabigyrate RID (J73) along its 5-fold axis and the relative stereographic net:
from the comparison with Fig. 3c one can note the 180°
rotation of the red
and yellow marks, placed on the most internal circumferences, representing the corresponding square and triangular faces
of the rotated cupolas. |
According to the 5m
point group, the 62 faces of the parabigyrate RID can be grouped, as shown in Fig.
20a, into five different 5-fold deltohedra (or trapezohedra), a 10-fold
prism and a pinacoid (or parallelohedron): the single forms with the same colour
have also an equal central distance.
The
intermediate steps in the reconstruction of the parabigyrate RID, given by the
intersection of the equidistant forms, are shown in
Fig. 20b, together with the resulting parabigyrate RID.
The pale-blue polyhedron consists in a dodecahedron, whereas, in the re-building
of the parabigyrate RID, the less usual red and yellow polyhedra play the same
role of the rhomb-triacontahedron and the icosahedron generating the
RID along with the dodecahedron (Fig.20c).






Rhomb-triacontahedron and icosahedron can be compared with the
corresponding red and yellow polyhedra in Fig. 20b.
The views of the dual of the parabigyrate RID
along the directions [010] and [τ 01]
are shown in Figure
21.
Consequently to the rotation of two opposite pentagonal cupolas in the
parabigyrate RID, in its dual there are two rings of ten faces (in dark-blue) having a
four-sided shape
different from the other forty faces (in pale blue) which are kite-shaped just like all the
faces of the Catalan deltoidal hexecontahedron, dual of the RID.
 |
 |
Fig. 21
The polyhedron dual of the parabigyrate RID, projected along
the directions: [010] (on the
left) and [τ 01]
(on the right). The twenty faces in dark-blue, distributed in two rings, have a four-sided shape: they differ from the forty kite-shaped faces, in pale blue, identical to the faces of the dual of the RID. | |
According to the
5m point group, in the dual of
the parabigyrate RID the sixty faces are grouped in four forms: two different pentagonal deltohedra, a dipentagonal
scalenohedron and a decagonal dipyramid (Fig. 22).
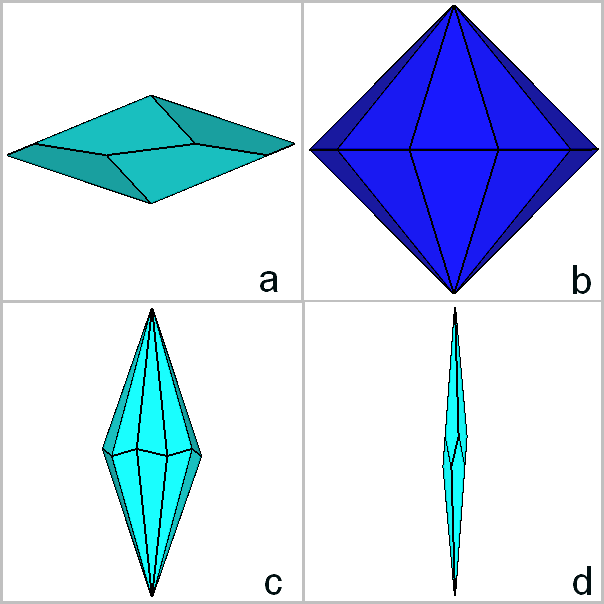 |
Fig. 22
View, along the
[010] direction, of the four forms (not drawn to scale), whose
intersection generates the dual of the parabigyrate RID. They are, in
sequence:
a) a flat pentagonal deltohedron b) a decagonal dipyramid c) a dipentagonal scalenohedron d) a sharp pentagonal deltohedron |
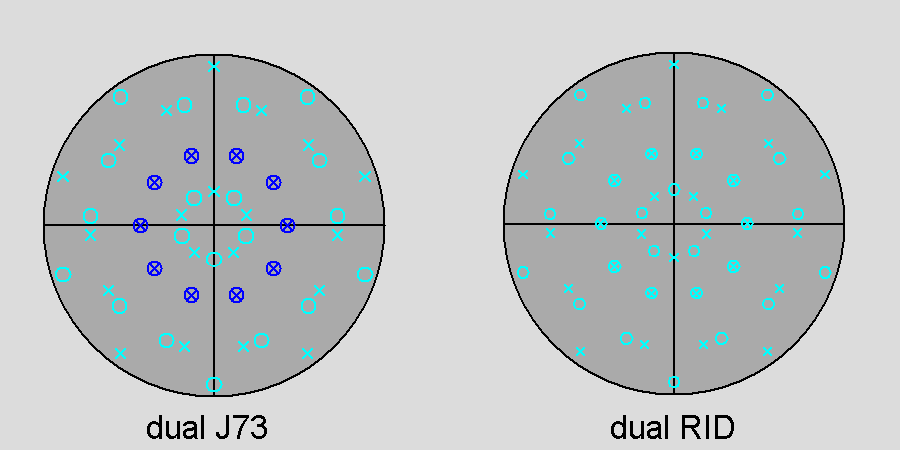 |
|
Fig. 23 - Comparison, along the [τ01] 5-fold axis, between the stereographic nets of the duals of parabigyrate RID (left)
and RID (right).
As a consequence of the 180° rotation of the fifteen vertices of both 5-fold cupolas, in the dual of the parabigyrate RID the faces of the flat 5-fold deltohedron undergo a corresponding rotation, whereas the 4-sided dark-blue faces of the 10-fold dipyramid belonging to the dual of J73 have, on the whole, the same orientation of the deltoidal pale-blue faces of the 10-fold dipyramid belonging to the dual of the RID: only the shape of the faces is different. |
 |
|
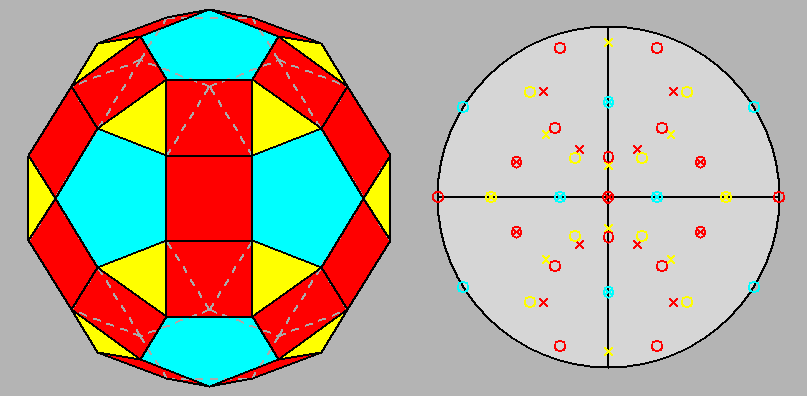
Fig. 24 - Metabigyrate RID obtained by a 180° rotation of the two highlighted pentagonal cupolas of a RID,
aligned along the |
 |
|
Fig. 25 - Clinographic view of the metabigyrate RID, showing the
two mirror planes and the 2-fold rotation axis placed at their intersection. |
 |
|
Fig. 26
Projection of the metabigyrate RID along the [001] 2-fold axis and the relative stereographic net:
from the comparison with Fig. 3a
relative to the RID, one can note
that, whereas in the RID all the red and yellow marks representing the
square and triangular faces non parallel to [001] are superimposed in pairs,
in the metabigyrate RID many of these marks are not superimposed,
due to the rotation of the two pentagonal cupolas. |
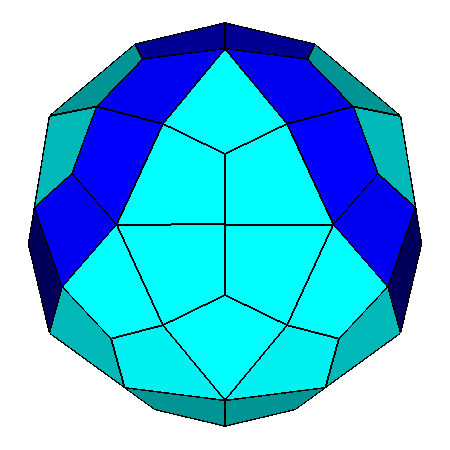
In Figure 27 one can see, on the left,
the projection along the directions [010]
of the dual of the metabigyrate RID and, on the right,
a clinographic view showing
also the two mirror planes intersecting along the [001]
2-fold axis.
Analogously to the orientation of the two rotated pentagonal cupolas
in J74, even in its dual the two rings of ten faces (in dark-blue), having a four-sided
but non deltoidal shape, are centered along the [τ
01] and [τ
01] directions: in particular, each face of a couple of contiguous faces of a ring shares a side with
a specular face belonging to the
other ring.
 |
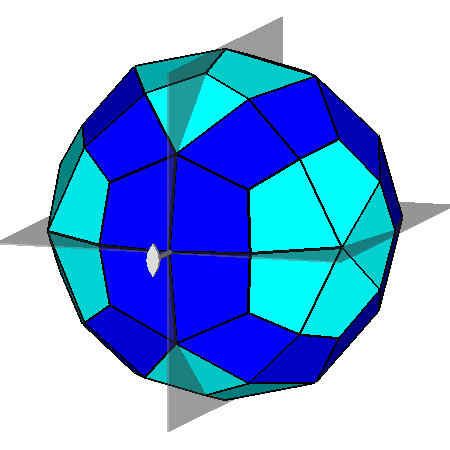 |
Fig. 27
Polyhedron dual of the metabigyrate RID:
on the left its projection along the [010] direction and, on the right,
a clinographic view showing the [001] 2-fold axis and the (100)
and (010) mirror planes
characterizing the mm2 point group. The twenty faces in dark-blue, having a four-sided but non-deltoidal shape, are arranged in two rings centered along the [τ01] and [τ01] directions. | |
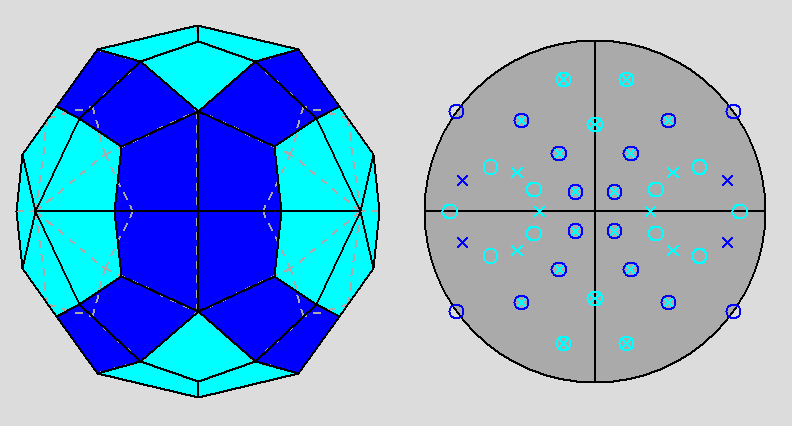
As one can infer from the stereographic net along the [001] 2-fold axis (Fig. 28),
in the dual of the parabigyrate RID the sixty faces
are arranged, according to the mm2 point group, into the following forms: twelve rhombic pyramids, four
dihedra (domes or sphenoids) and a rhombic prism.
 |
|
Fig. 28
Projection, along the [001]
2-fold axis, of the dual of the metabigyrate RID and relative stereographic net; in mm2 point
group
the sixty faces are arranged into the following forms: twelve rhombic pyramids,
four sphenoids (or domes or dihedra) and a rhombic prism (it should be compared with
Fig. 7a). |
 |
|
Fig. 29 - View along the [111] 3-fold axis, at the
intersection of three mirror planes, of the
trigyrate RID, obtained by a 180° rotation of three pentagonal cupolas of
a RID
aligned along the equivalent |
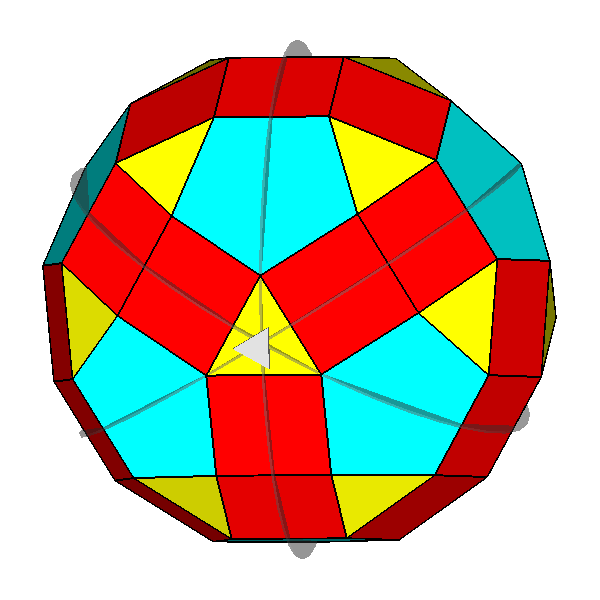 |
Fig. 30
View of the trigyrate RID including
the three mirror planes which intersect along the 3-fold axis perpendicular to the
(111) triangular face. In consequence of the rotation of the three pentagonal cupolas, a side is shared by each square face of the rotated cupolas with a square face that has not been rotated. |
 |
|
Fig. 31
Projection of the trigyrate RID along the 3-fold axis normal to the
(111)
triangular face and the relative stereographic net (to be compared with Fig. 3b). |
The polyhedron dual of the trigyrate RID is shown in Fig.32, where also the three mirror planes intersecting along the
3-fold axis are reported.
 |
|
Fig. 32 - View of the dual of the trigyrate RID including
three mirror planes intersecting along the [111]
3-fold axis. |
 |
|
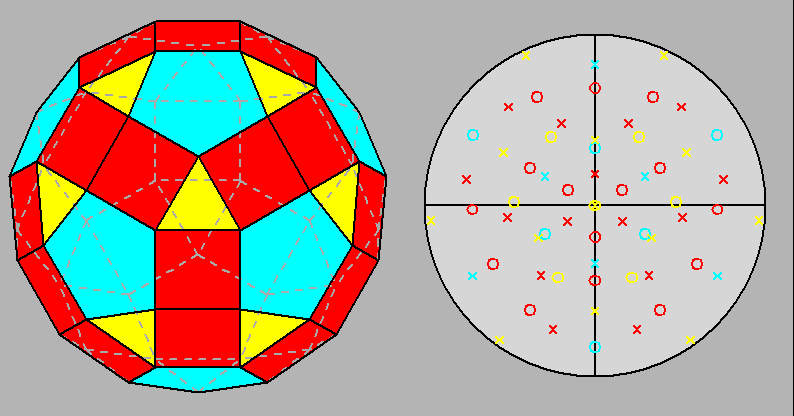
Fig. 33 - Projection of the dual of the trigyrate RID along the [111] 3-fold axis
and relative stereographic net showing that its sixty faces are arranged into four trigonal and eight ditrigonal pyramids
(to be compared with Fig. 7b). |
 |
|
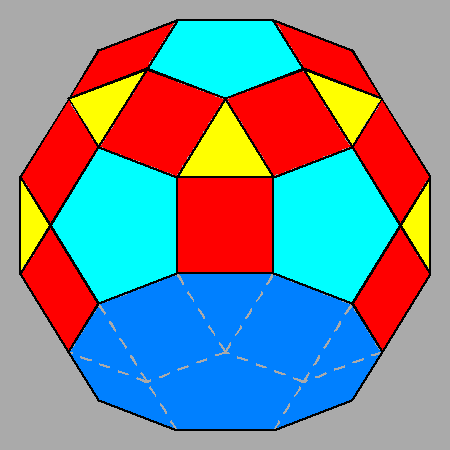
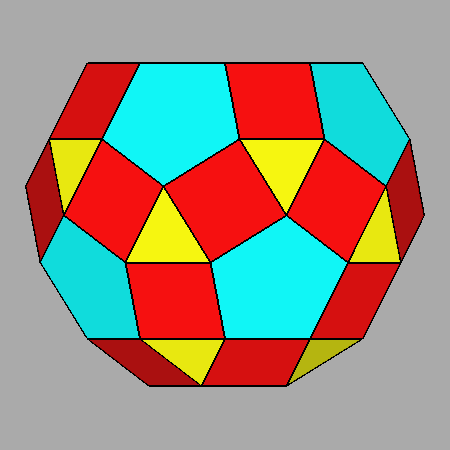
Fig. 34 - The removal of a pentagonal cupola from the
RID leads to the diminished RID, a regular-faced polyhedron in which a
regular decagon substitutes the pentagonal cupola. |
 |
 |
|
Fig.35 -
Views of the diminished RID along the [001] (left) and [010]
(right) directions making an angle of 58.28° and 90°, respectively, with the normal
to the [τ 0 1] axis of the removed cupola. | |
 |
|
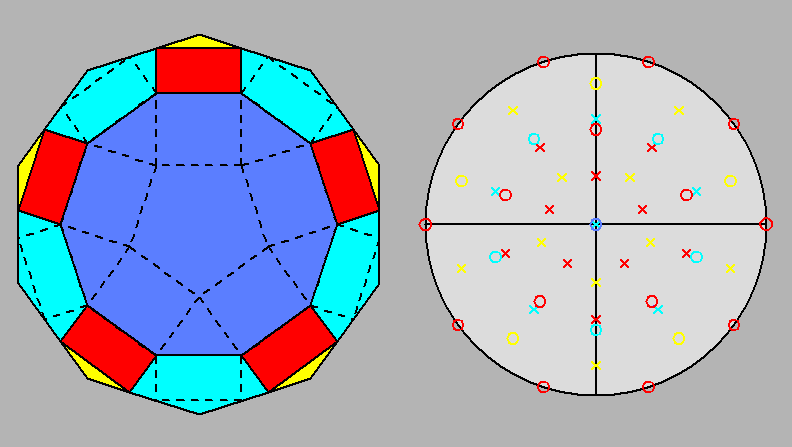
Fig. 36 - Projection of the diminished RID along the 5-fold axis normal to the decagonal face
(on the left) and relative stereographic net
(on the right); it should be compared with Fig. 3c.
|
 |
|
Fig. 37 - Clinographic view of the dual of the diminished RID,
showing the ten triangular face forming a 10-fold pyramid. |
The dual of J76, shown in Figure 37 in the same orientation
as J76 in Figure 34, is rather different from the dual of the RID
and also from the duals of its isomers: the lack in J76 of the five vertices of the pentagon belonging to the removed cupola implies the lack of five faces
in the dual;
consequently the ten faces contiguous to the missing ones extend their
dimension. They share a
vertex placed along the
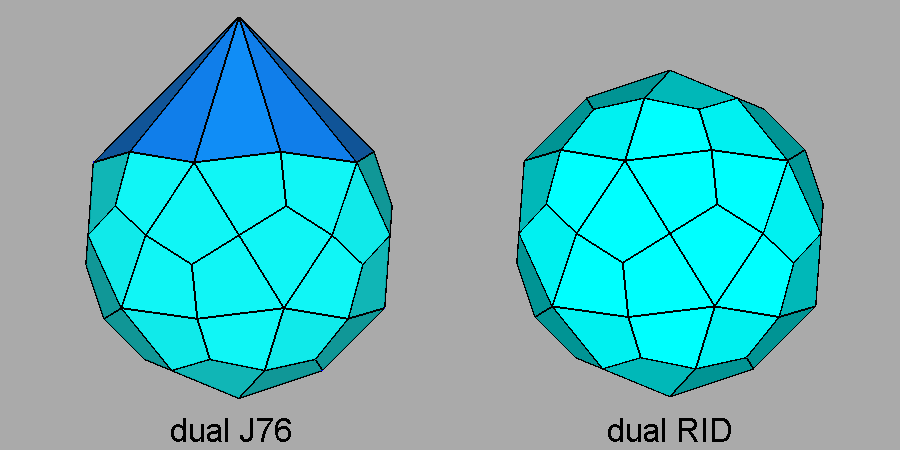 |
|
Fig. 38 - View along the direction [010]
of the dual of the diminished RID compared with the dual of the RID. |
 |
|
Fig. 39 - Projection of the dual of the diminished RID along the
[τ01]
5-fold axis (on the left) and relative stereographic net
(on the right).
It is not difficult to recognize the presence of five mirror planes
which characterize the 5m point group, together with the |
 |
|
Fig. 40 - The removal of a pentagonal cupola and
the simultaneous rotation of the opposite pentagonal cupola transform
the
RID into the paragyrate diminished RID, which includes a decagonal face in
substitution of the removed pentagonal cupola. |
 |
|
Fig. 41 - View of the paragyrate diminished RID along the
[010] direction, perpendicular to a square face and also to the axis of
both removed and rotated 5-fold cupolas. |
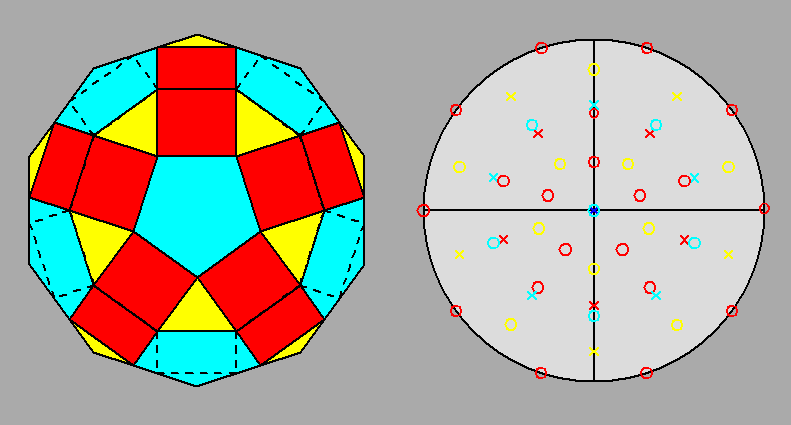
In Figure 42 one can see the view of J77, along the 5-fold axis of the rotated and removed cupolas,
together with the corresponding stereographic net.
 |
|
Fig. 42 - Projection of the paragyrate diminished RID along the 5-fold axis normal to the
pentagonal face of the rotated |
The simultaneous rotation and diminution do not introduce in J77 variations of symmetry in respect to the gyrate RID or the diminished RID: therefore also the paragyrate diminished RID can be described in the 5m point group and its fifty-two faces can be grouped, analogously to J76, in eleven forms: eight pentagonal pyramids, a decagonal prism and two monohedra (or pedions).
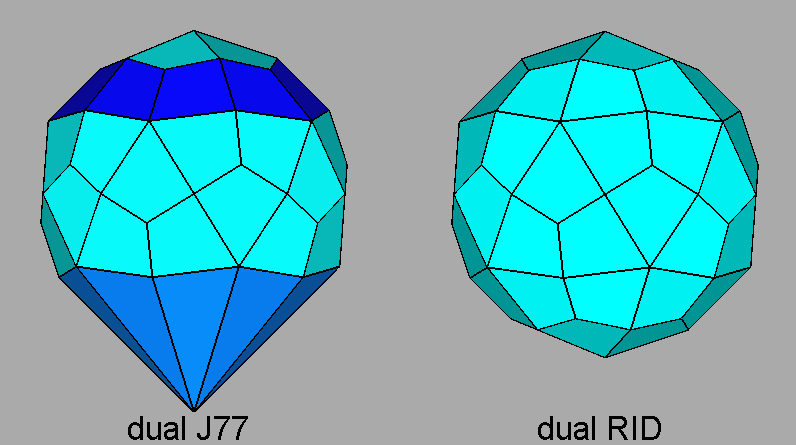
Figure 43 shows (on the left) the dual of J77 and (on
the right) the dual of the RID, viewed along the [010] direction.
 |
|
Fig.43 - The dual of the paragyrate diminished RID (on the left),
compared with the dual of the RID (on the right), shows the two 10-fold pyramidal forms, consisting of ten triangular faces
in blue
and ten four-sided, but non-deltoidal, faces
in dark-blue, which shape is different from the shape of
the deltoidal faces in pale-blue. |
 |
|
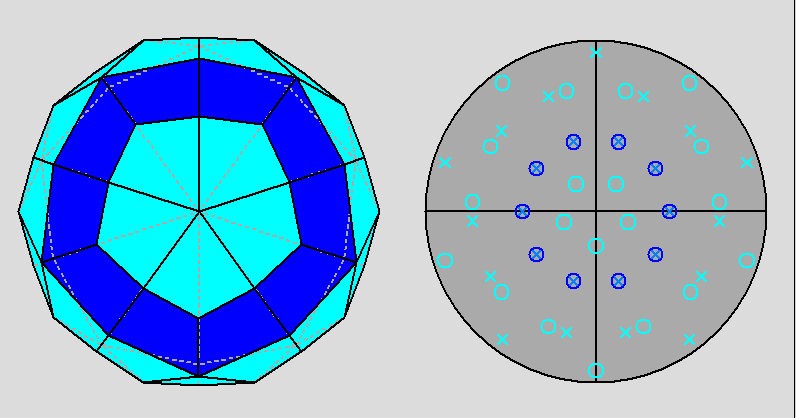
Fig. 44 - Projection of the dual of the paragyrate diminished RID along the
[τ01]
5-fold axis (on the left) and relative stereographic net
(on the right).
It is not difficult to recognize the presence of the five mirror plane
characterizing, together with the 5-fold axis, the 5m point group. |
 |
|
Fig. 45 - The removal of a 5-fold cupola and
the simultaneous rotation of another one, aligned along a direction
making an angle of 116.56° with the axis of the previous
cupola,
transform the RID into the metagyrate diminished RID, which includes a
decagonal face in substitution of the removed pentagonal cupola. |
The removal from the RID of a pentagonal
cupola, accompanied by the simultaneous rotation of another one, can be
accomplished also when the axes of the two cupolas, instead of being
aligned as in J77, form an angle φ
= 2arctg(τ) = 116.56° (equal to the angle between the two rotated
cupolas in J74): the resulting polyhedron is the metagyrate diminished
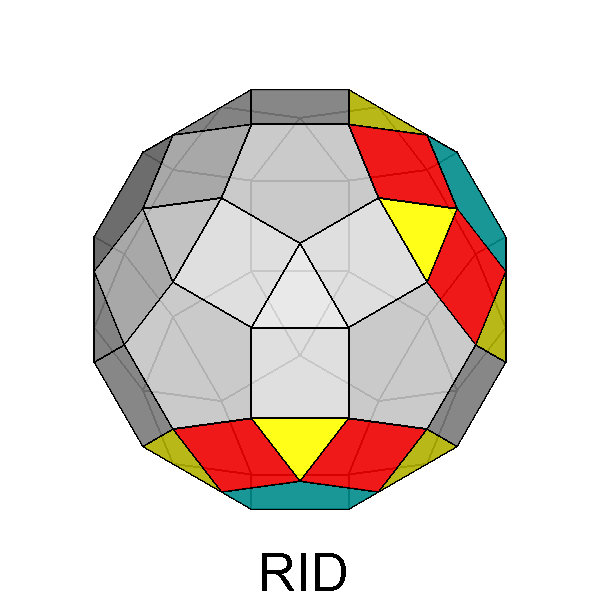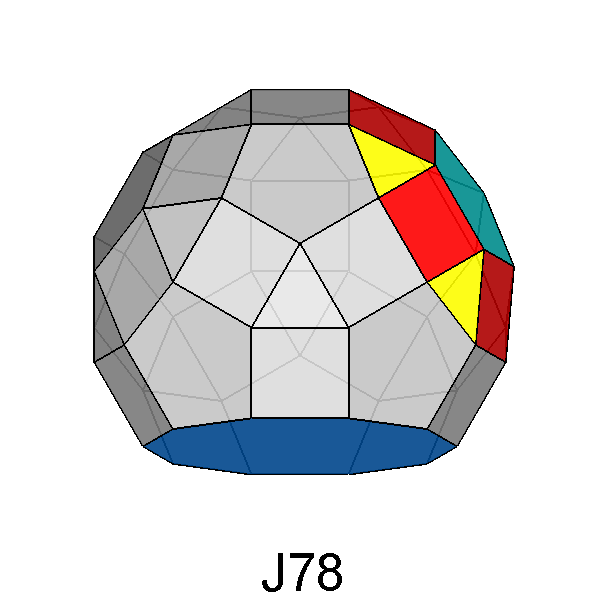
RID (J78), reported in Figure 45.
Its view along the [010] direction, perpendicular to both axes of the cupolas, is shown in Figure 46.
 |
|
Fig. 46 - View of the metagyrate diminished RID along the [010] direction,
perpendicular to the axes of both rotated and removed 5-fold cupolas, which
make
an angle of 116.56°, being aligned along the [τ
01] and [τ 01]
directions. |
 |
|
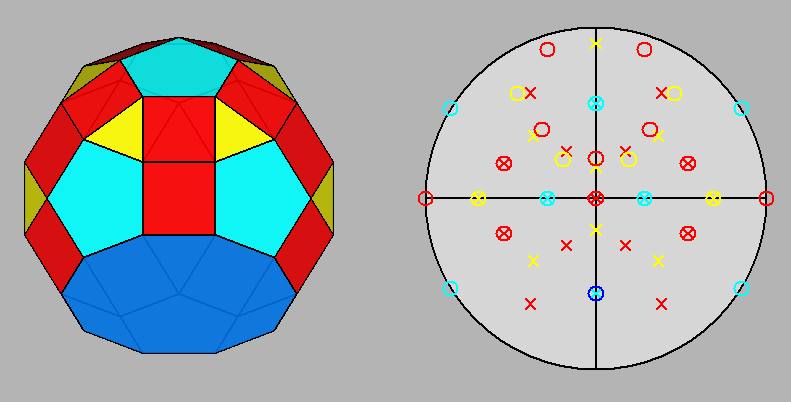
Fig. 47 - Projection of the metagyrate diminished RID along the
[001]
direction (on the left) and relative stereographic net
(on the right): only a vertical
(010)
mirror plane is present.
It should be compared with Fig. 3a.
|
 |
|
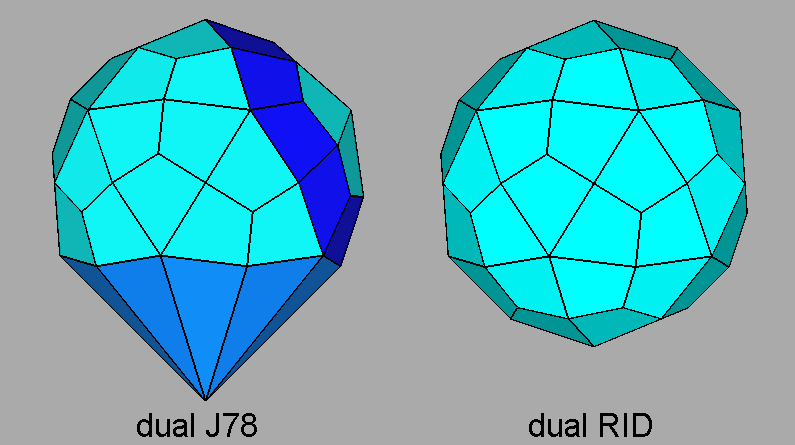
Fig. 48 - View along the
[010]
direction of the dual of the metagyrate diminished RID compared with the dual
of the RID.
|
 |
|
Fig. 49 - Projection of the dual of the metagyrate
diminished RID along the
[001]
direction (on the left) and relative stereographic net
(on the right). The presence of a
(010)
mirror plane placed vertically is easily recognizable. |
 |
|
Fig. 50 - Bigyrate diminished RID derived from the RID
when two of a set of three 5-fold cupolas (each other at 116.56°) are
rotated and the third one is removed: a decagonal face replaces the removed pentagonal
cupola. |
 |
|
Fig. 51 - Comparison between the bigyrate
diminished RID (on the left) and the RID
(on the right) viewed along the
[1 0 τ] direction, normal to
the axis of the removed 5-fold cupola; the positions of the two rotated cupolas are symmetrical in respect to the vertical (010)
mirror plane, the only symmetry operator present in J79. |
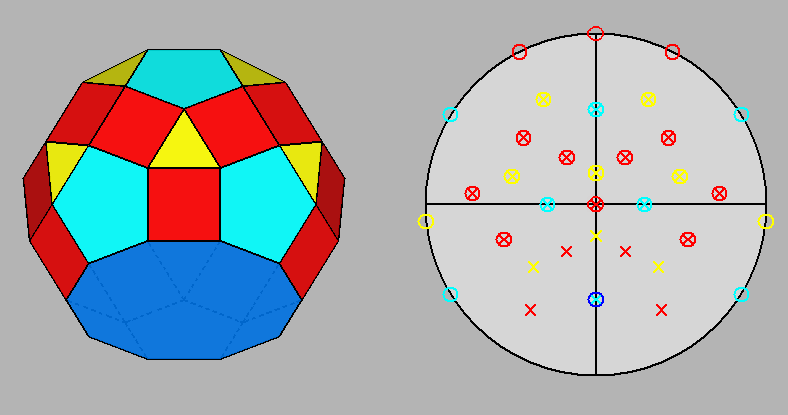 |
|
Fig. 52 - View along the [001]
direction of J79 (left) and relative stereographic net
(right); the two rotated cupolas are
symmetrical in respect to to the vertical (010)
mirror plane. |
 |
|
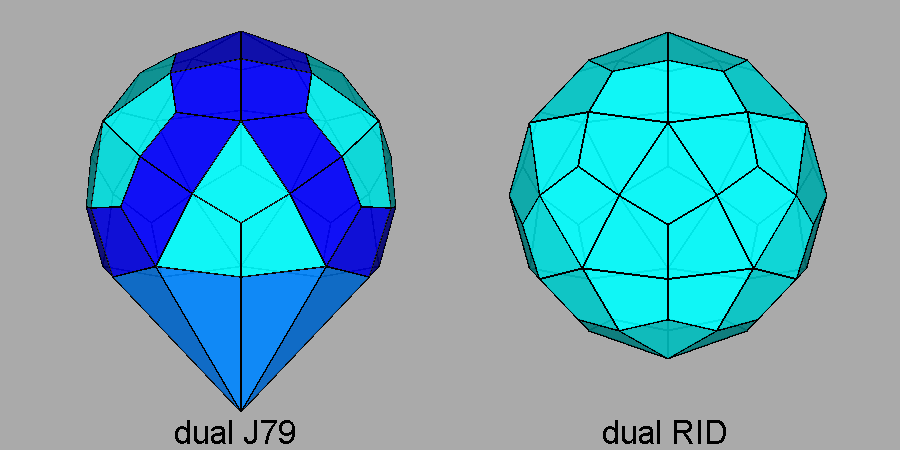
Fig. 53 - Views, along the [10τ] direction, of the dual of the bigyrate diminished RID
(on the left) and of the dual of the RID, shown
on the right by comparison. |
 |
|
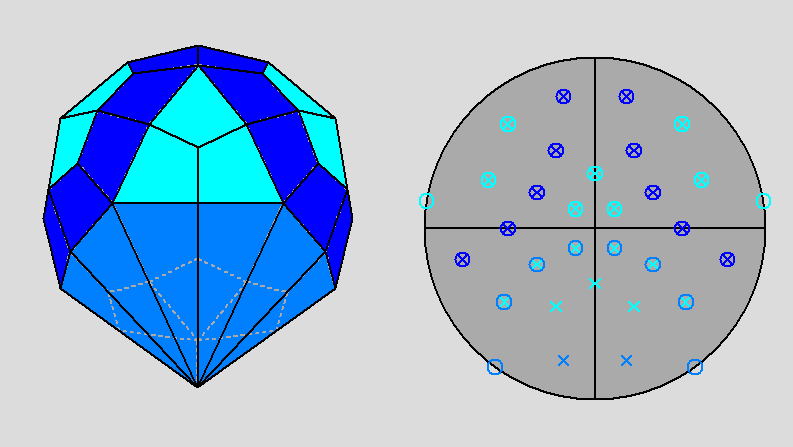
Fig. 54 - View, along the [001]
direction, of the dual of J79 (left) and relative stereographic net
(right).
Also in this case, the presence of a (010) mirror plane placed vertically is easily recognizable. |
 |
|
Fig. 55 - The simultaneous removal of two
opposite pentagonal cupolas of the RID leads to the parabidiminished RID,
which includes two decagonal faces in substitution of the removed pentagonal cupolas. |
 |
 |
|
Fig. 56 - Comparison between the parabidiminished RID (on the left),
and the parabigyrate RID (on the right): their projections along the [010] direction
show the removal or the rotation of two opposite 5-fold cupolas centered along
the
[τ 0 1]
and [τ 0
1] opposite directions.
As one can infer from the presence of the 5-fold axis and the five couples made of a 2-fold axis and an orthogonal mirror, both Johnson's polyhedra belong to the 5m point group. | |
 |
|
Fig. 57 - View along the [τ 0 1]
direction of the parabidiminished RID (left) and
relative stereographic net
(right).
In addition to the evident five mirror planes intersecting along the 5-fold rotation axis directed along [τ 0 1], also five |
 |
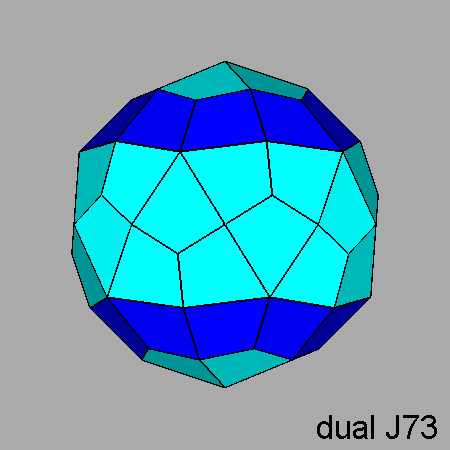 |
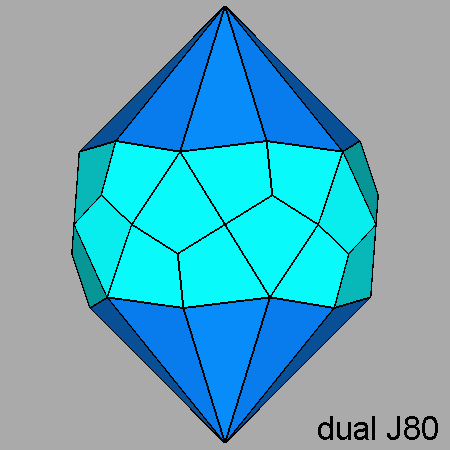
Fig. 58 - Comparison between the dual of the parabidiminished RID (on the left)
and the dual of the parabigyrate RID (on the right):
in the former, a decagonal dipyramid, consisting of twenty triangular blue faces,
replaces the decagonal dipyramid, consisting of dark blue | |
 |
|
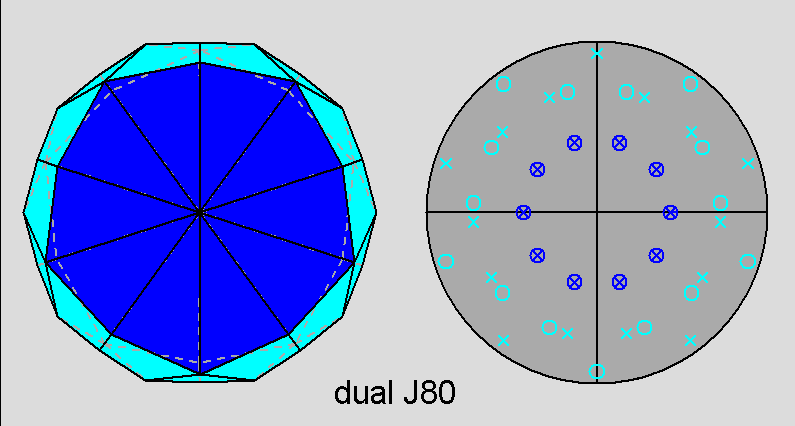
Fig. 59 - View along the [τ 0 1]
direction, corresponding to the 5-fold rotation axis, of the dual
of the parabidiminished RID (left) and relative stereographic net
(right). |
 |
|
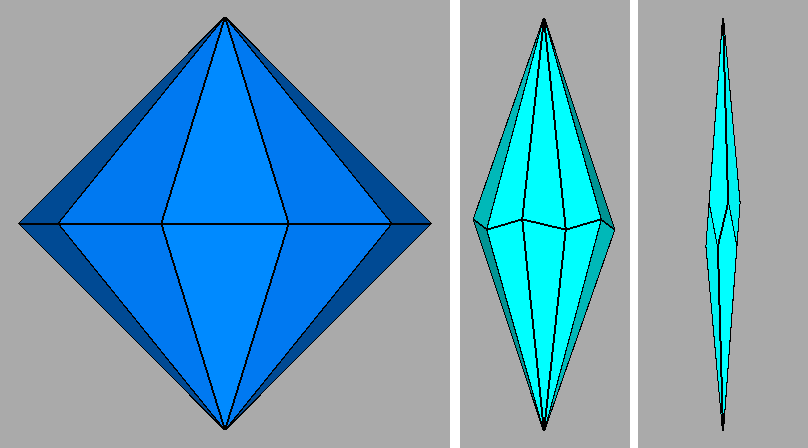
Fig. 60 - From left:
the 10-fold dipyramid, the dipentagonal scalenohedron and the sharp pentagonal deltohedron whose intersection,
in case of faces having the same central distance, generates the dual of the parabidiminished RID. This figure can be
compared with Fig.22, where one
can see that, among the single forms deriving from the decomposition
of the dual of the parabigyrate RID, also a flat pale-blue deltohedron
was present.
|
 |
|
Fig. 61 - The simultaneous removal from the RID of two
pentagonal cupolas, aligned along two directions making an angle of
116.56°, leads to the metabidiminished RID. |
 |
 |
|
Fig. 62 - The views of the metabidiminished RID along two
orthogonal directions: [010] (on the left)
and [001] (on the right), highlight the presence of two orthogonal mirror planes
intersecting along the [001] 2-fold axis. | |
 |
 |
|
Fig. 63 - Stereographic net of J81 along the directions
[010]
(a) and [001] (b), showing the presence of two orthogonal
mirror planes., intersecting along the [001] 2-fold axis. | |
 |
 |
|
Fig. 64 - Views of the dual of the metabidiminished RID along the orthogonal directions [010]
(a)
and [001] (b), highlighting the presence of two orthogonal
mirror planes intersecting along the [001] 2-fold axis. | |
 |
 |
|
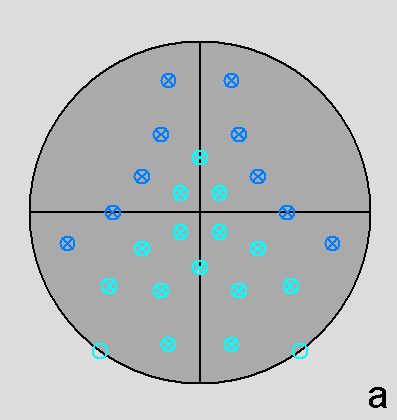
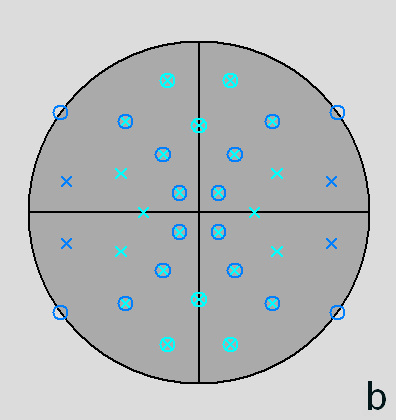
Fig. 65 - Stereographic projections of the dual of the metabidiminished RID along the orthogonal directions [010]
(a) and [001] (b). The stereographic net (a) is
symmetric in respect to a vertical (010) mirror plane, whereas in (b)
both vertical (010) and horizontal (100) mirror planes,
intersecting along the [001] 2-fold axis, are highlighted. | |
 |
|
Fig. 66 - Removal of two cupolas
and simultaneous rotation of the third one leading to the gyrate
bidiminished RID. |
_J82_along_ 001.png) |
_J82_along_ 1_0_tau.png) |
_J82_along_tau_0_1.png) |
_J82_along_ 100.png) |
|
Fig. 67 - Views of the gyrate bidiminished RID along four
directions: in addition to the orthogonal directions, [001] (a) and [100] (d),
both normal to a square face,
the intermediate directions are: [10 τ ] (b),
normal to the axis of the rotated cupola, and
[τ 0 1] (c),
normal to a pentagonal face. All the views highlight the presence of an only mirror plane, orthogonal to the [010] direction; the (a) and (d) views can be compared with the (a) and (b) views in Fig.62, relative to the metabidiminished RID, which is characterized by the the removal of two 5-fold cupola, without any rotation of the third cupola. | |
 |
 |
|
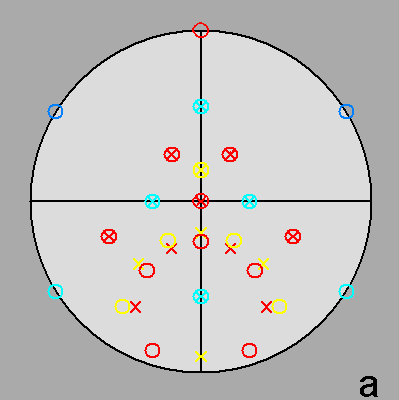
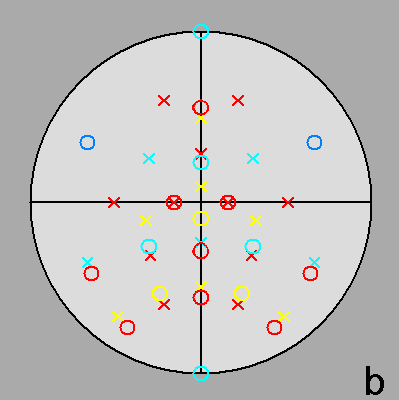
Fig. 68 - Stereographic projections of the gyrate bidiminished RID along the directions [001]
(a) and [10
τ ] (b) | |
_dual_J82_along_ 001.png) |
_dual_J82_along_ 10_tau.png) |
_dual_J82_along_ tau_01.png) |
_dual_J82_along_ 100.png) |
|
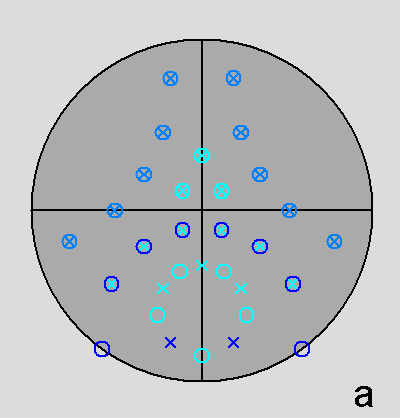
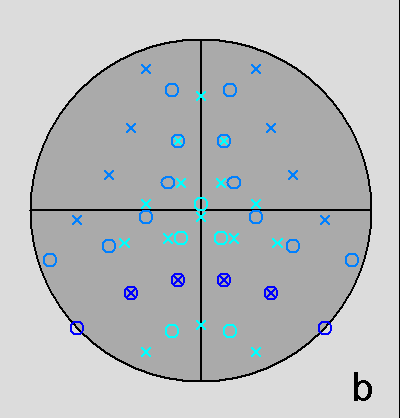
Fig. 69 - Views of the dual of the gyrate bidiminished
RID along the same four directions of Fig.67: in addition to the
orthogonal directions, [001]
(a) and [100]
(d),
the intermediate directions are
[10 τ ]
(b) and [τ 0 1] (c). | |
 |
 |
|
Fig. 70 - Stereographic projections of the dual of the gyrate bidiminished RID along the directions [001]
(a) and [10
τ ] (b). | |
 |
|
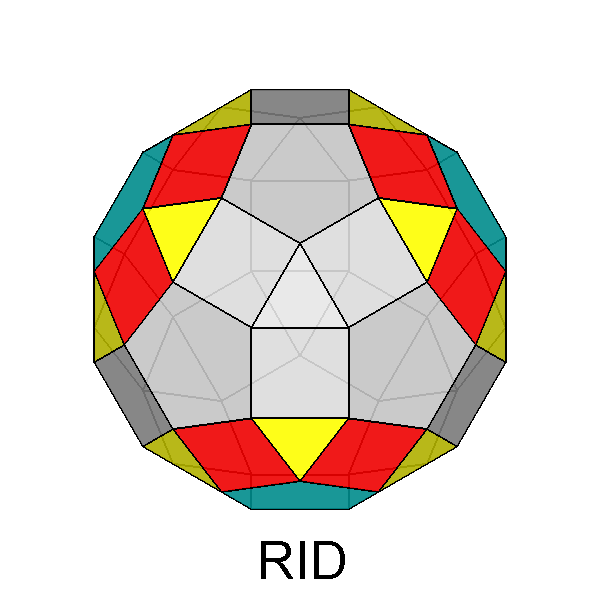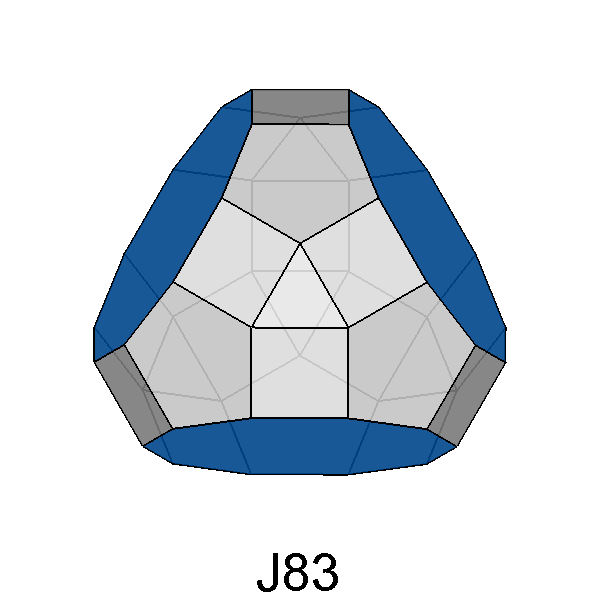
Fig. 71 - The simultaneous removal of three pentagonal
cupolas of the RID (each other at 116.56°) leads to the tridiminished
RID, which includes three decagonal faces in substitution of the removed pentagonal cupolas.
|
 |
||
|
Trigyrate RID (J75) |
| |
 |
 |
 |
|
Bigyrate diminished RID (J79) |
RID |
Gyrate bidiminished RID (J82) |
 |
||
|
Tridiminished RID (J83) |
||
|
Fig. 72 - The four Johnson polyhedra obtained from the RID by
a 180° rotation and/or removal of three | ||
 |  |
 |
 |
|
Fig. 73 - Views of the tridiminished RID and corresponding stereographic nets: (a) along the 3-fold axis, at the intersection of three mirror plane (b) along a direction orthogonal to the axes of the two decagonal faces replacing the 5-fold cupolas. | |
The dual of J83
includes three 10-fold triangular faces deriving, by a duality relation, from the vertices of the three
decagonal faces belonging to J83.
Two views of the dual of J83 and the respective stereographic nets are shown in Figure
74.
 |
 |
|
Fig. 74
Views of the tridiminished RID (left) and relative stereographic nets
(right):
(a) along the 3-fold axis, at the intersection of three mirror plane (b) along a direction perpendicular to the axes of two 10-fold pyramids and making an angle of 58.28° with the axis of the third 10-fold pyramid. |
The features of the Johnson's polyhedra
deriving from the RID and also of their duals, including the number
of faces of the single forms in which each polyhedron can be decomposed,
are resumed in the next table.
Despite the different notation, the classification of the
Johnson's polyhedra according to the respective point group is analogous to the
classification given by
Norman Johnson in his fundamental paper [2] concerning the convex
polyhedra with regular faces.
|
Decomposition in single forms of both the Johnson's polyhedra derived from the RID and their duals |
||||||||
| Johnson's polyhedra |
Single forms |
Faces |
Total |
Point
group |
Duals of Johnson's polyhedra |
Single forms |
Faces |
Total |
|
J72 |
10 pentagonal pyramids |
5 |
62 |
5m |
dual J72 |
4 pentagonal pyramids |
5 |
60 |
|
J73 |
5 pentagonal deltohedra 1 decagonal prism 1 parallelohedron |
10 |
62 | 5m | dual J73 |
2 pentagonal deltohedra |
10 |
60 |
|
J74 |
9 rhombic pyramids 1 rhombic prism 9 dihedra 1 parallelohedron 2 monohedra |
4 |
62 | mm2 | dual J74 |
12 rhombic pyramids |
4 |
60 |
|
J75 |
5 ditrigonal
pyramids 10 trigonal pyramids 2 monohedra |
6 |
62 | 3m | dual J75 |
8 ditrigonal pyramids |
6 3 |
60 |
|
J76 |
8 pentagonal pyramids 1 decagonal prism 2 monohedra |
5 |
52 | 5m | dual J76 |
3 pentagonal pyramids |
5 10 10 |
55 |
|
J77 |
8 pentagonal pyramids 1 decagonal prism 2 monohedra |
5 |
52 | 5m | dual J72 |
3 pentagonal pyramids |
5 10 10 |
55 |
|
J78 |
20 dihedra 10 monohedra 1 parallelohedron |
2 |
52 | m | dual J78 |
26 dihedra |
2 1 |
55 |
|
J79 |
21 dihedra 10 monohedra |
2 |
52 | m | dual J79 |
26 dihedra |
2 1 |
55 |
|
J80 |
3 pentagonal deltohedra 1 decagonal prism 1 parallelohedron |
10 |
42 |
5m | dual J80 | 1 decagonal
dipyramid 1 dipentagonal scalenohedron 1 pentagonal deltohedron |
20 |
50 |
|
J81 |
5
rhombic pyramids 1 rhombic prism 7 dihedra 1 parallelohedron 2 monohedra |
4 |
42 |
mm2 |
dual J81 |
10 rhombic pyramids 1 rhombic prism 3 dihedra |
4 |
50 |
|
J82 |
15 dihedra 12 monohedra |
2 |
42 |
m |
dual J82 |
23
parallelohedra 4 monohedra |
2 |
50 |
|
J83 |
1
ditrigonal pyramid 8 trigonal pyramids 2 monohedra |
6 |
32 |
3m |
dual J83 |
6 ditrigonal pyramids 3 trigonal pyramids |
6 |
45 |
The duals of the Johnson's polyhedra
derived from the RID are listed in Figure 75, in the same
sequence of the Johnson's polyhedra reported in Figure 10, namely:
| FIG. 75a | |||
 |
 |
 |
 |
|
Dual of gyrate RID (J72) |
Dual of parabigyrate RID (J73) |
Dual of metabigyrate RID (J74) |
Dual of trigyrate RID (J75) |
| FIG. 75b | |||
 |
 |
 |
 |
|
Dual of diminished RID (J76) |
Dual of parabidiminished RID (J80) |
Dual of metabidiminished RID (J81) |
Dual of tridiminished RID (J83) |
| FIG. 75c | |||
 |
 |
 |
 |
|
Dual of paragyrate diminished RID (J77) |
Dual of metagyrate diminished RID (J78) |
Dual of bigyrate diminished RID (J79) |
Dual of gyrate bidiminished RID (J82) |
| Fig. 75 - Duals of all the Johnson's polyhedra (except the pentagonal cupola) deriving from the RID. | |||
 |
|
Animation showing the dual of the RID and the duals of the Johnson's polyhedra derived from the RID by the rotation and/or removal of its pentagonal cupolas. |
The procedure leading to twelve Johnson's polyhedra, by rotation and/or removal of up to three
When a cupola is removed from the RID, eleven faces (one pentagonal, five
triangular and five square faces) are replaced by a decagonal face:
consequently, the number of faces decreases from sixty-two to fifty-two,
forty-two or thirty-two, depending on the number of cupolas eliminated.
Both rotation and removal of cupolas from the RID imply a change of the
symmetry: it decreases from m
3
5 in the RID to:
1)
Peter R. Cromwell
Polyhedra,
Cambridge University Press, 1997
2) Norman W. Johnson
Convex Polyhedra with Regular Faces, Canadian Journal of Mathematics,
18, 169-200, 1966
3) http://www.mi.sanu.ac.rs/vismath/zefiro2009/___pseudo_RCO_Zefiro-Ardigo'.htm
4)
http://www.mi.sanu.ac.rs/vismath/zefirocorrection/__Zefiro-Ardigo'_icosahedral_polyhedra_updating.htm
5)
http://www.georgehart.com/virtual-polyhedra/archimedean-duals-info.html
 |
 |
|
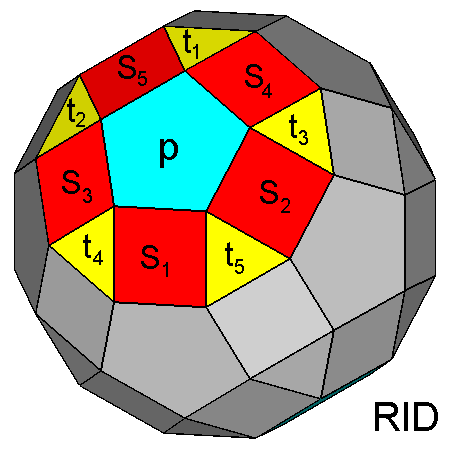
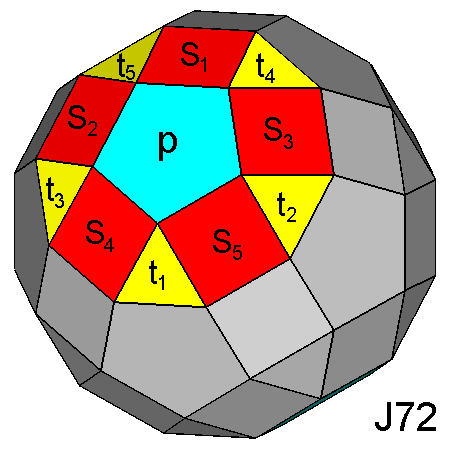
Labelling of the faces of
the5-fold cupolas, aligned along the [τ 01] direction,
belonging to the RID (on the left) or to the
gyrate RID (on the right): p
= pentagonal face, Si = square faces,
ti = triangular faces.
The different orientation of each face, except
p, derives from the 180° rotation of the
cupola around its [τ 01] axis. | |
|
Indices of the corresponding pentagonal, square and triangular faces of the RID and J72 | |
| RID | J72 |
| p (τ01) | p (τ01) |
| S1 (100) | S1 (102) |
| S2 (τ 1 1/τ) | S2 (5τ-7 -3τ+4 1) |
| S3 (τ -1 1/τ) | S3 (5τ-7 3τ-4 1) |
| S4 (1 1/τ τ) | S4 (7τ+4 -5 3-τ) |
| S5 (1 -1/τ τ) | S5 (7τ+4 5 3-τ) |
| t1 (1/τ 0 τ) | t1 (5τ+2 0 -1) |
| t2 (1 -1 1) | t2 (3 2τ-1 1) |
| t3 (1 1 1) | t3 (3 -2τ+1 1) |
| t4 (τ -1/τ 0) | t4 (1 3τ-4 2) |
| t5 (τ 1/τ 0) | t5 (1 -3τ+4 2) |
 |
 |
A duality relation subsists among the five labelled kite-shaped faces
belonging to the dual of the RID (on
the left) and the five vertices of the pentagonal face, perpendicular to
the [τ 01] direction,
of the RID
. As a consequence of the 180° rotation, occurring in J72, of the fifteen vertices of the 5-fold
cupola aligned along [τ 01]
, in the dual of J72 the relative dual faces rotate accordingly
(on the right). The final result is a 180° rotation of the five labelled faces, whereas the contiguous ten faces (making a ring) apparently do not rotate, being 180° a multiple of 360° /10. The different shape of the ten faces in the dual of J72 is due solely to the intersection with the 180° rotated five faces. | |
|
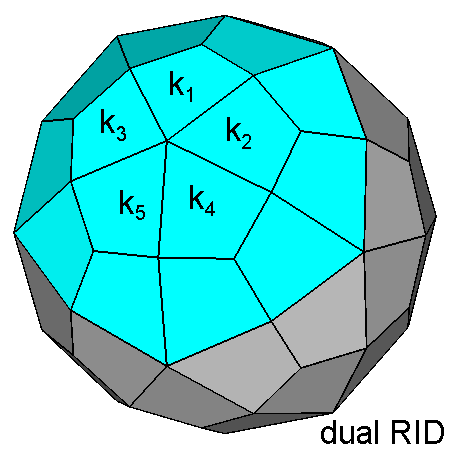
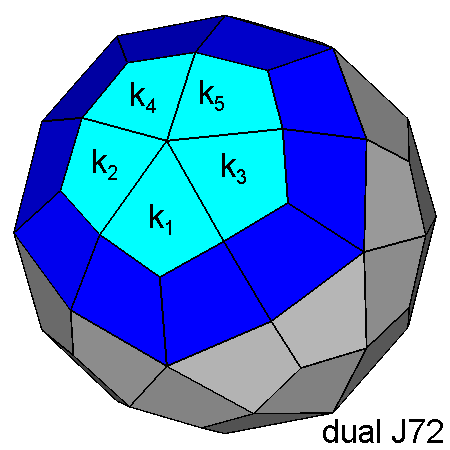
Indices of ki = kite-shaped faces in the duals of the RID and (after a 180° rotation) of J72 | |
| DUAL of the RID | DUAL of J72 |
| k1 (τ 0 τ +1/τ) | k1 (5τ-2 0 1) |
| k2 (2 1 τ) | k2 (6τ+2 -5 7τ-6) |
| k3 (2 -1 τ) | k3 (6τ+2 5 7τ-6) |
| k4 (τ2 1/τ 1/τ) | k4 (8τ+1 -5 6τ+7) |
| k5 (τ2 -1/τ 1/τ) | k5 (8τ+1 5 6τ+7) |
Geometrical features of the faces characterizing the duals of the Johnson's polyhedra derived from the RID
The geometrical
features of the faces characterizing the duals of the
Johnson's polyhedra derived from the RID can be determined starting from the dual of
the diminished rhomb-icosidodecahedron (J76),
having fifty-five faces: in fact it
numbers forty-five of the sixty kite-shaped faces present in the dual of the RID, and, in substitution of the other fifteen faces,
ten triangular 10-fold faces forming a pyramid.
The truncation of such pyramid, in correspondence to its apex, by a flatter
5-fold pyramid (having kite-shaped faces) leads to different results depending on the orientation of this
5-fold pyramid.
If the faces of the 5-fold pyramid are
orientated as the corresponding faces in the dual of the RID, the
truncation of the ten triangular faces leads to as many
kite-shaped faces: consequently, the sixty congruent kite-shaped faces resulting
altogether constitute
the deltoidal hexecontahedron, dual of the RID.
The truncation of the 10-fold pyramid (having triangular faces), with the same
5-fold pyramid, but 180° rotated along its axis, gives as result ten 4-sided faces
which, together with the other fifty faces, constitute the dual of J72.
 |
|
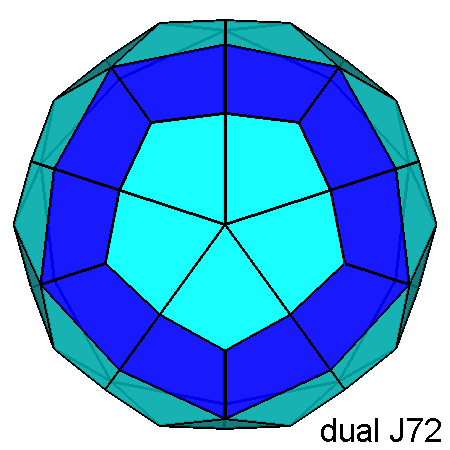
Animation showing the truncation of the triangular faces of the 10-fold pyramid present in the dual of J76 by the kite-shaped faces of a flatter 5-fold pyramid: it gives rise to the dual of the RID or, after a 180° rotation along its axis, to the dual of J72. |
 |
 |
 |
|
dual RID |
dual J76 |
dual J72 |
 |
 |
 |
 |
 |
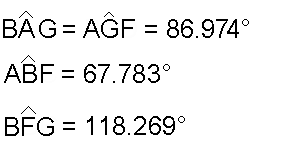 |
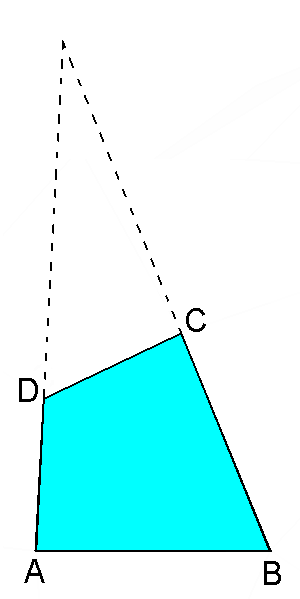
|
AB =
BC=1 AD = CD = 0.6496 = 3/(τ+3)
|
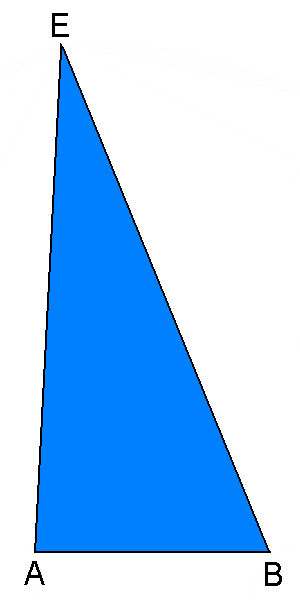
AB =
1
AE = 2.1708 = 3(τ+2)/5 BE = 2.3416 = 2(3τ+1)/5
|
AB =
1
FG = 0.6496 = 3/(τ+3) AG = 0.8292 = 3/(τ+2) BF = 0.8204 = (6τ+4)/(6τ+7) |
The set of four values of the angles in the
kite-shaped and in the 4-sided faces are identical, but their sequence is
different: in the kite-shaped faces belonging to the dual of the RID the two equal angles
(having the intermediate value) are opposite each other, whereas
they are contiguous in the 4-sided faces belonging to the dual of J72.
Two angles of the triangular faces belonging to the dual of J76 are equal to the corresponding angles present in the faces of
both duals of J72 and RID, whereas the third angle of the triangular faces has a
smaller value.
A side having the same length of the two long sides of the kites which
characterize the dual of the RID is also present both in the
In the dual of J72 the other two sides of the 4-sided faces have lengths intermediate
between the lenghts of the first two sides, equal to the sidelengths of the
kites, whereas in the dual of J76 the length of the other two sides
of the triangular faces more than double the length of the first side, having the same length
of the long side of the kites.