In this paper our attention will be focused on the Escher's solid.
As a first step, let's try to answer to the question: which are the single polyhedra constituting it? A possible answer would seem to be: three rotated octahedra (also taking into account that the compound of three octahedra is the dual of the compound of three cubes [4,5]).
Starting from the red {111} octahedron shown in Fig. 2, a 90° rotation around the [110] direction leads to the yellow octahedron.
A second 90° rotation of the red octahedron around the [110] direction leads to the pale-blue octahedron.
The association of the three octahedra generates a compound polyhedron that clearly does not coincide with the solid placed on top of the right tower in the Escher drawing.

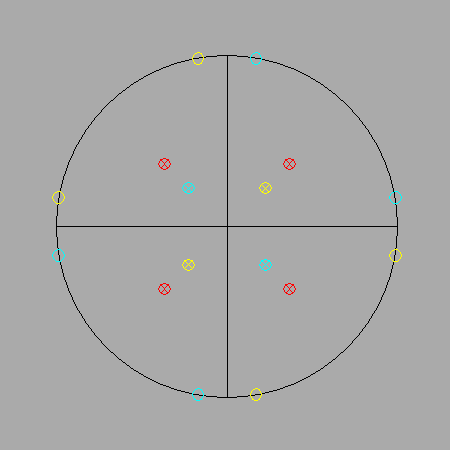
The views of the compound of three octahedra along a 2-fold and a 3-fold axis are reported in  the upper row of Fig. 3; the further view along a 4-fold axis and the corresponding stereographic projection of its faces are reported in the lower row.

In order to get the Escher's solid, it is necessary to substitute a flatter square dipyramid for the octahedron.
Then, in Fig. 4,the animated sequence made of seventeen frames shows a series of compounds of 3 square dipyramids, obtained decreasing progressively the angle between the normal to the dipyramidal faces and the vertical [001] 4-fold axis, from 54.74° = arccos(1/√3), angle between the normal to the {111} faces of the octahedron and the [001] direction, to the final value of 45° = arccos(1/√2).
Considering a monometric system of Cartesian axes, in correspondence of such 45° angle the Miller's indices relative to the square dipyramid assume the values {11√2}; the association of this dipyramid with two other square dipyramids, obtained by 90° rotations around the [110] and [110] directions, reproduces exactly the Escher solid.
The presence of an irrational value among the Miller's indices is due to the fact that we are not dealing with a crystal, which would be subject to the Hauy's law stating that the ratios of the indices are rational numbers.
The faces of the square dipyramid generating the Escher's solid are isosceles triangles, in which the ratio R between each of the two equal sides and the third side corresponds to √3 /2 (as one can infer from geometrical considerations relative to Escher's solid, leading to R² - (1/2)² = (1/2)² + (1/2)² ; consequently, in the isosceles triangles the two equal angles measure 54.74° = arccos(1/√3).

The left column of Fig. 5 shows, in succession, the initial {111} octahedron, the final {11√2} square dipyramid and an animated stereographic projection illustrating the transition between the two single forms; in turn, the right column shows the compound of three octahedra, the Escher's solid and an animated stereographic projection illustrating the transition between the two compounds.

It is interesting to note that the skeletal forms of both compounds appear in different versions of Escher's wood engraving Stars (1948) : the compound of three dipyramids, together with other polyhedra, in a preliminary study of the work [6], whereas the compound of three octahedra is the main subject of the final version [7].
Fig. 6 shows the remake, along the same angle of view, of both skeletal compounds of three polyhedra drawn by Escher in the successive versions of Stars.

Substantially, the octahedron can be described as a particular square dipyramid whose faces have the shape of equilateral triangles; because of the presence of four 3-fold axes normal to the faces, in addition to the three 4-fold axes, the six 2-fold axes, the nine mirrors and the inversion center [7], the relative point group symmetry is 4/m 3 2/m.
The faces of each other square dipyramid are instead isosceles triangles: it implies the absence of the 3-fold axes and therefore the relative symmetry is lower than the symmetry of the octahedron.
When all the generic {hkl} forms, neither parallel nor perpendicular to the [001] 4-fold axis, are square dipyramids, the corresponding point group symmetry is 4/m.

 Applying to the {11√2} square dipyramid a 45° clockwise rotation around the vertical [001] axis, one obtains a congruent form characterized by the more usual {101} Miller's indices: in fact, assuming again a monometric system of Cartesian axes, the (101) face of the dipyramid intersects equal parameters on [100] and [001] axes.
The animated views of the square dipyramids involved in the 45° rotation and their stereographic representation are shown in Fig. 7 .

Analogously to the procedure previously adopted for the {111} octahedron, a 90° rotation of the red {101} square dipyramid around the [100] direction leads to a yellow square dipyramid; another 90° rotation of the red dipyramid around the [010] direction leads to a pale-blue square dipyramid (Fig. 8).
The Escher's solid deriving from the square dipyramids in this new orientation is shown in the fourth image of Fig. 8.

In the upper row of Fig. 9 one can see the three compounds made of two square dipyramids, intermediates between the single dipyramid and the Escher's solid.
In each case, four couples of faces belonging to different square dipyramids are partially overlapped: the shared surfaces, differently coloured, have a rhombic shape (with the ratio between the length of the diagonals equal to √2).
As a consequence, the intersection of the three square dipyramids corresponds to a rhomb-dodecahedron (viceversa, the stellation of the rhomb-dodecahedron generates the Escher's solid [3]). In the lower row of Fig. 9 one can see, on the left, the rhomb-dodecahedron which results from the intersection of the three square dipyramids generating the Escher's solid drawn on the right.
The central image of the lower row represents the stereographic projection, along the [001] direction, of the rhomb-dodecahedron and also of the faces of the Escher's solid.

Six further views of the Escher's solid are visualized in Fig. 10: the views along the [001] 4-fold axis, the  [111] 3-fold axis and the [110] 2-fold axis (in each case with the [110] direction set vertically) in the upper row, the related clinographic views in the lower row.

Applying also to the {111} octahedron a 45° rotation around the vertical [001] axis, one obtains a congruent form characterized by the irrational {√201} Miller's indices.
The animated views of the octahedra involved in the 45° rotation and their stereographic representation are shown in Fig. 11.

• in the first row: in the center, the red {√201} octahedron and, sideways, the yellow and the pale-blue octahedra obtained by 90° rotations around the [100] and [010] directions, respectively
• in the second row: the three compounds of two octahedra (to be compared with the three compounds of two square dipyramids drawn in Fig. 9).
  One can note that they are congruent by 90° rotations around the cartesian axes:
  • a 90° rotation around [001] involves the compound made of the red and the yellow octahedra and the compound made of the red and the pale-blue octahedra
  • a 90° rotation around [100] involves the compound made of the red and the pale-blue octahedra and the compound made of the yellow and the pale-blue octahedra
  • a 90° rotation around [010] involves the compound made of the yellow and the pale-blue octahedra and the compound made of the red and the yellow octahedra
• in the third row: the three solids, derived from the intersection of each couple of octahedra, they too congruent by 90° rotations around the cartesian axes; their sixteen faces consist of eight trapezoids (or trapezia) and eight kites (or deltoids).
  Their main geometrical features are the following:
  • the inner angles of the trapezoids measure 112.21° and 67.79° (ratio between the length of the parallel sides equal to 2)
  • the angle between the short sides of the kites measures 98.21°
  • the angle between the long sides of the kites measures 78.46°
  • the two angles between the sides of the kites having different length measure 91.66°.
• in the fourth row: the relative stereographic projections; as evidenced by the central image, 4/m 2/m 2/m is the maximum point symmetry that can be associated both to a compound of two octahedra and to the solid resulting from their intersection.
  The 4-fold axis is associated to the [010], [001] and [100] direction for the red and pale-blue, yellow and pale-blue, red and yellow couples of octahedra, respectively.

The solid derived from the intersection of the three octahedra corresponds to the {√201} tetrakis-cube (or tetrakis-hexahedron), polyhedron with 24 faces that can be derived from a cube in which, by a process of  cumulation [9] (or augmentation [10]), a square pyramid grows on each face of the cube. In Fig. 13 one can see, on the left, the tetrakis-cube, on the right the compound of 3 octahedra of which the tetrakis-cube is the intersection, and, in the center, the stereographic projection along [001], common to both: the relative point symmetry is 4/m 3 2/m, higher than the 4/m 2/m 2/m point symmetry of the compound of two octahedra and of the solid resulting from their intersection.
One can notice that the orientation of all the rotation axes relative to the compound of three octahedra derived from the initial red {√201} octahedron is the usual orientation of the rotation axes in the 4/m 3 2/m cubic point group, relative also to the tetrakis-cube: 4-fold axis along [100], 3-fold axis along [111], 2-fold axis along [110], and the respective equivalent directions.
On the other hand, in case of the association of three octahedra starting from the {111} octahedron, as shown previously in the stereographic projection of Fig. 3, the orientation of the rotation axes looks uncommon: 4-fold axis along [110], 3-fold axis along [0 √2 1], 2-fold axis along [010] and the respective equivalent directions.
In practice, the different orientation in the two cases of the axes of symmetry consists in a 45° rotation around the [001] direction.

Incidentally, one must avoid to mistake the previous {√201} tetrakis-cube for the Catalan {201} tetrakis-cube, dual of the Archimedean truncated octahedron [11,12], in which the height of the square pyramids augmenting the faces of the cube is lower than in {√201} tetrakis-cube.
In Fig. 14, the Catalan tetrakis-cube is drawn in the upper row, on the left: it corresponds to the intersection of three square dipyramids, whose compound, derived from the red {201} square dipyramid, is shown on the right.
The dual of the Catalan tetrakis-cube is the Archimedean truncated octahedron shown in the lower row, on the left, together with the compound of an octahedron and a cube of which it is the intersection; the ratio between the central distances of the octahedral and cubic faces is equal to √3/2.

Even if, as already pointed out, the (101) face of the square dipyramid and the (111) face of the octahedron make different angles with the vertical [001] direction, both belong to the zone of the [101] direction, like so, in case of the 4/m point group, all the square dipyramids {hkh} with 0 < k/h < 1, intermediate between the {101} dipyramid and the {111} octahedron.
The left column of Fig.15 reports a series of six polyhedra from the {101} square dipyramid to the {111} octahedron, passing through the {hkh} dipyramids: {414}, {525}, {212}, {434}; the series on the right includes the corresponding compounds of 3 polyhedra, from the Escher's solid to the compound of three octahedra.