Description of the Forms Belonging to the 235 and m35 Icosahedral Point Groups Starting from the Pairs of Dual Polyhedra: Icosahedron-Dodecahedron and Archimedean Polyhedra-Catalan Polyhedra
|
TETRAHEDRON |
CUBE |
OCTAHEDRON |
DODECAHEDRON |
ICOSAHEDRON |
 |
 |
 |
 |
 |
|
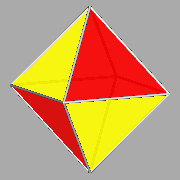
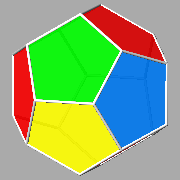
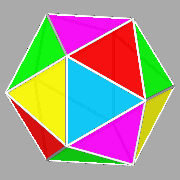
FIG.1 - The five regular
convex polyhedra (or Platonic solids), coloured in order to evidence the
single faces. | ||||
Two further Archimedean polyhedra, whose faces belong to different sets of three regular polygons:
The duals of all the previous Archimedean polyhedra are the following Catalan polyhedra:
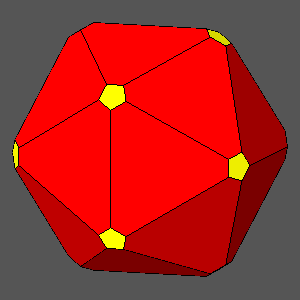
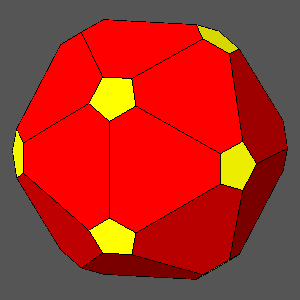
The
hexakis-icosahedron is the sole with 120 asymmetric faces; unlike all the other
forms it is compatible only with the m35
point group, whereas another Catalan polyhedron, the
pentagonal hexecontahedron, made of 60 pentagonal faces (each symmetric with respect to a mirror plane),
belongs only to 235, the other icosahedral point group.
The dual of the pentagonal hexecontahedron is the
snub dodecahedron, Archimedean polyhedron with a
rather singular look, resulting from the intersection of the three following forms:
The absence of mirror planes and centre of symmetry implies that, because of enantiomorphism, in this case there are two chiral couples of dual polyhedra: each couple is made of a snub dodecahedron and a pentagonal hexecontahedron, both right or left.
 |
 |
|
FIG.5 - Couple of dual polyhedra: Catalan pentagonal hexecontahedron (on the left) and Archimedean snub dodecahedron (on the right).
| |
In all the icosahedral polyhedra
made of different forms, the
positions, with respect to the reference axes, of dodecahedral, icosahedral and rhomb-triacontahedral faces are
always fixed, being perpendicular to the axes characterizing the
icosahedral symmetry: 5-fold, 3-fold and 2-fold rotation axes, respectively.
On the other hand, each other single generic form has usually an orientation different from the one
of the corresponding Catalan polyhedron, and it is subject only to the
condition:
 |
 | ||
 |
 |
 |
 |
| Rhombic triacontahedron | Icosahedron | Deltoid-hexecontahedron | Hexakis-icosahedron |
|
FIG.6 - Pair of polyhedra deriving from the intersection of the same four forms: The relative extent of the four forms changes in the two polyhedra, as a consequence of the variation of each central distance. | |||
It is useful to examine in
detail the associations of symmetry operators characterizing the
icosahedral point groups, also with the intent to evidence their relationships
with the classic crystallographic points groups.
On the whole, the symmetry operators present in 235 point group (or crystal class)
consist of:
![]()
(where α, β, γ indicate the angles of rotation, around an
appropriate direction, by which all the crystallographic elements, and the whole
crystal form, superimpose) lets one
obtains the possible angles ω between each couple of such
directions.
In particular, concerning 5-fold axes, one obtains that the least angles between:
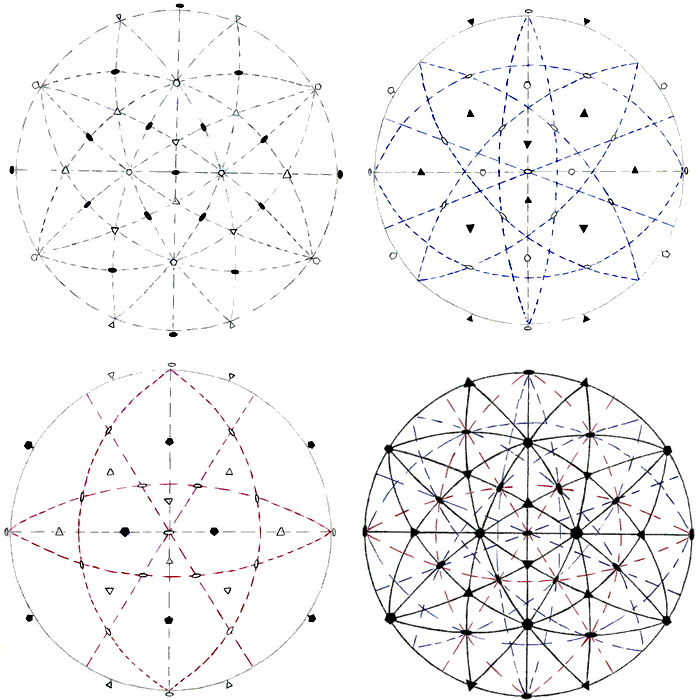 |
FIG.7 - Free-hand drawing of the stereographic
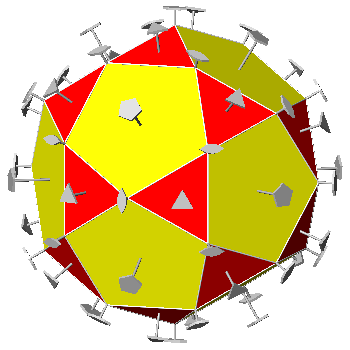
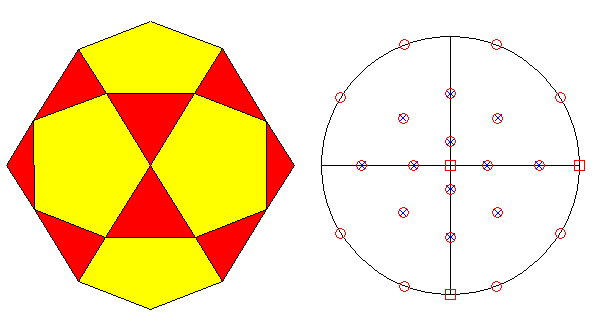
projections of the icosahedral symmetry operators. In addition to the position of 2-fold, 3-fold and 5-fold rotation axes: are sequentially reported in the four images. |
Analogously to
what happens for the crystallographic 23 point group, subgroup of 235
point group,
three mutually orthogonal 2-fold axes (chosen among
five set of three) play
the role of reference axes.
The values of all the
angles formed between each pair of rotation axes are reported in the following
table.
|
| |||
| 2 | 3 | 5 | |
| 2 | 36° | 20.91° | 31.72° |
| 2 | 60° | 54.74° | 58.28° |
| 2 | 72° | 69.10° | 90° |
| 2 | 90° | 90° | |
| 3 | 41.81° | 37.38° | |
| 3 | 70.53° | 79.19° | |
| 5 | 63.44° | ||
As one can see, the different least values of the angles not concerning 5-fold axes are the
following:
DUAL FORMS CHARACTERIZING THE ICOSAHEDRAL POINT GROUPS
Each of the six forms placed in a particular orientation (parallelism and
sometimes also orthogonality), as regards the symmetry operators, is compatible
with both 235 and m35
point groups; on the contrary, the seventh form, that is in general position, results
different in the two point groups, also concerning multiplicity, because of the presence in the m35 point group of
both the fifteen mirror planes and the centre of symmetry, all absent in the 235 point group.
Both dodecahedron and icosahedron are convex regular polyhedra (or
Platonic solids): their faces are made of twelve regular pentagons
orthogonal to the 5-fold axes, and twenty equilateral triangles orthogonal to
the 3-fold axes, respectively; in both polyhedra 2-fold axes pass in the middle point of every
edge.
The icosahedron can also be
considered as the result of the intersection of five tetrahedra:
The action
of the set of symmetry elements over each face placed orthogonally to a 2-fold
axis generates the rhombic triacontahedron (or rhomb-triacontahedron), made up of thirty rhombic faces. The
ratio between the lengths of the diagonals of the faces corresponds to the
golden ratio τ.
(Analogously one can note the existence, in the cubic system, of a somehow
similar form, the rhombic dodecahedron {110}, made up of twelve rhombic faces.
The ratio between the lengths of the diagonals of the faces in this case
corresponds to the value √2).
Analogously to the icosahedron, also the rhombic triacontahedron is made up of faces whose indices derive from two
different sets of indices:
{100} and
The rhombic triacontahedron belongs to the family of Catalan polyhedra (so named
after the Belgian mathematician Eugène Charles Catalan) made up by equal
faces, having generally the shape of symmetric but non-regular polygons, and different regular
angoloids. The duals of the isohedral Catalan polyhedra are the isogonal semiregular Archimedean polyhedra, in turn characterized
by faces made up by two or three different regular polygons (whose sides and
angles are therefore all equal) and by equal but non-regular angoloids.
It must be pointed out that, just as it happens with the other dual pairs
consisting of an Archimedean polyhedron and a Catalan polyhedron, the ratio
between the central distances of the triangular and pentagonal faces of the
icosi-dodecahedron is the reciprocal of the ratio between the central distances
of the two different vertices of the dual rhombic triacontahedron, lying
along the 3-fold and 5-fold axes, respectively.
Since, in the
instance of the dual pair consisting of triacontahedron and icosi-dodecahedron, the
total number of faces and vertices corresponds to
30 + 32 = 62, the edges are sixty in both polyhedra,
according to the rule: F+V=E+2.
There are two other semiregular polyhedra, both
deriving from the intersections between icosahedron and dodecahedron, of which
the icosi-dodecahedron just described can be considered an intermediate form:
they are the
Archimedean truncated icosahedron and the Archimedean truncated dodecahedron.
In a generic truncated icosahedron, the icosahedral faces truncated
by the pentagonal faces of dodecahedron assume firstly the shape of non-regular
hexagons (Fig.14): nevertheless they are symmetric relatively to three mirror lines, forming each other
angles of 60°, which intersect in the centre of the faces.
When the ratio between the central distances of dodecahedral and icosahedral faces
assumes the following value: After the Archimedean truncated
icosahedron, as a consequence
of the further truncation of the
icosahedron by the dodecahedron, one obtains, in addition to dodecahedral faces with the shape of
regular pentagons, icosahedral faces having again the
shape of non-regular but symmetric hexagons, as shown in Fig.14; the length of the three
shorter sides of hexagon decreases progressively, till it vanishes when the
hexagonal faces turn into the
equilateral triangular faces of the icosidodecahedron.
The dual of the Archimedean truncated icosahedron is the Catalan
pentakis-dodecahedron, whose faces are named by indices deriving from the cyclic permutation,
changes of sign included, of three sets of indices:
The Catalan pentakis-dodecahedron can be supposed to derive from a
dodecahedron, substituting each face with a pentagonal pyramid having
the height H given by the relation:
In addition to the Catalan pentakis-dodecahedron dual of the Archimedean truncated
icosahedron, there are very many other generic pentakis-dodecahedra (duals of the
truncated icosahedra different from the Archimedean one) all
including faces {hk0} characterized by a ratio between the indices h and k such
that:
In relation to the dual pair consisting of truncated icosahedron and pentakis-dodecahedron, the
total number of faces and vertices corresponds to:
TRUNCATED DODECAHEDRON AND TRIAKIS-ICOSAHEDRON
As a consequence of the beginning of the truncation by the triangular faces of
an icosahedron,
the pentagonal faces of a dodecahedron become
DODECAHEDRON ARCHIMEDEAN ICOSIDODECAHEDRON
Only when the ratio between the central distances of the two forms becomes equal to: the faces of the dodecahedron assume the shape of regular decagons,
thus obtaining the Archimedean truncated dodecahedron,
in which each vertex is shared by three regular polygons: two decagons and a triangle. After the Archimedean
truncated dodecahedron, as a consequence of the further
truncation of the dodecahedron by the icosahedron, one obtains, in addition to icosahedral
faces with the shape of equilateral triangles, dodecahedral faces having again
the shape of non-regular but symmetric decagons; the length of the
five shorter sides of decagon decreases progressively, till it vanishes when the
decagonal faces turn into
the regular pentagonal faces of the icosi-dodecahedron.
The dual of the
Archimedean truncated dodecahedron is the Catalan
triakis-icosahedron (or
trisicosahedron), whose faces are named by indices deriving from the cyclic permutation,
changes of sign included, of three sets of indices:
Consequently it consists of 12+24+24 =
60 faces having
the shape of an isosceles triangle, such that:
The Catalan
triakis-icosahedron can be supposed to derive from an icosahedron, substituting
each face with a trigonal pyramid having the following height
H: In this relation L is the
length of the side of the triangular base of the pyramid, namely the icosahedral
face.
In addition to the Catalan triakis-icosahedron, dual of the Archimedean
truncated dodecahedron, there are vey many other generic triakis-icosahedra (duals of the
truncated dododecahedra different from the Archimedean one) all including faces
{hk0} characterized by a ratio between the indices h and k such that:
The heights of the trigonal pyramids, relative to all the different triakis-icosahedra, range between:
Since the total number of faces and vertices corresponds to:
TRUNCATING ICOSI-DODECAHEDRON BY RHOMBIC TRIACONTAHEDRON
The truncation, by means of a rhombic triacontahedron, of all the vertices of
an icosi-dodecahedron
(polyhedron a in Fig.22),
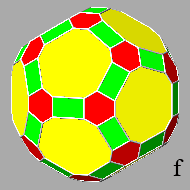
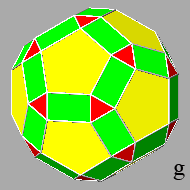
at the beginning transforms the triangular and pentagonal faces of the icosi-dodecahedron into hexagonal and decagonal polygons, respectively, both non-regular
even though symmetric,
whereas the faces of the triacontahedron assume a rectangular shape (ref: polyhedra
Decreasing the central distance of the triacontahedral faces, one obtains the
polyhedron g, whose faces, besides the
rectangular ones, consist of equilateral triangles and regular pentagons as well
as the initial faces of the icosi-dodecahedron, but orientated in an opposite
direction.
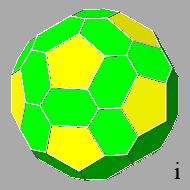
After the elimination of the icosahedral triangular faces, the remaining faces
are the dodecahedral pentagonal faces and the
triacontahedral faces which from octagonal become hexagonal, always non-regular
but symmetric: the six sides of the hexagonal faces consist of four short sides and two long sides (ref: polyhedron
i).
TWO FURTHER SEMIREGULAR POLYHEDRA: TRUNCATED ICOSI-DODECAHEDRON AND RHOMBICOSI-DODECAHEDRON
The Archimedean truncated icosi-dodecahedron and
the
rhombicosi-dodecahedron are the two further semiregular
polyhedra which, as just described, cannot be obtained truncating directly an
icosi-dodecahedron by means of a rhombic triacontahedron, but, more generally,
derive from the intersection of the three forms:
icosahedron, dodecahedron and rhombic triacontahedron, taking into account
possible intermediate steps as described in Fig.23.
Regarding the Archimedean truncated icosi-dodecahedron (name that, for the aforementioned
reasons, is not entirely appropriate and consequently it is sometimes replaced
by "great rhombicosidodecahedron"), the icosahedral, dodecahedral and triacontahedral
faces become regular hexagonal, regular decagonal and square ones, respectively,
when the ratios between each pair of central distances assume the following values:
ddodecahedron
/ dicosahedron = (1+1/τ2)√1+1/τ2
/√3= 0.9380
dicosahedron / dtriacontahedron = √3 /(1+ 2
/τ2) = 0.9819
ddodecahedron
/ dtriacontahedron = √1+1/τ
2(1+1/τ2) /(1+2/
τ2) = 0.9210
ddodecahedron
/ dicosahedron = (3√3
/ [(τ2+2)√1+1/
τ2] = 0.9571
dicosahedron
/ dtriacontahedron
= (1+ 2 /τ2)
/√3
= 1.0184 ddodecahedron
/ dtriacontahedron = 3/
(τ2
√1+1/τ2) = 0.9748
The first three rows of Fig.23 report the different combinations of each pair of
polyhedra, from which both the Archimedean truncated icosi-dodecahedron and the
rhombicosi-dodecahedron (on the left and on the right of the fourth row,
respectively) can be generated, as a consequence of the intersection with the
remaining third polyhedron (when the ratios between the respective central
distances assume just the aforementioned values.
Generation of an Archimedean truncated
icosi-dodecahedron (left) and a rhombicosi-dodecahedron (right)
by the combination of a dodecahedron, an icosahedron and a rhombic
triacontahedron FIG.23a - Intermediate step given by the
intersection of a dodecahedron and an icosahedron
ddod. /dicos.
= (1+1/τ2)
√1+1/τ2
/√3 = 0.9380 ddod. /dicos. =
3√3 / [(5-1/τ2)
√1+1/
τ2] = 0.9571 FIG.23b - Intermediate step given by the intersection of
an icosahedron and a triacontahedron dicos. /dtriacont. = √3/(1+2/τ2)= 0.9819 dicos. /dtriacont.
= (1+2/τ2)/√3
= 1.0184 FIG.23c - Intermediate step given by the intersection of
a dodecahedron and a triacontahedron ddod. /dtriacont.
= √1+1/τ2(1+1/τ2)/(1+2/τ2)
= 0.9210 ddod. /dtriacont.
= 3/(τ2√1+1/τ2) = 0.9748 On
the basis of the previous considerations, one does not have to draw the conclusion
that the Archimedean truncated icosi-dodecahedron and the rhombicosi-dodecahedron
are totally unrelated to the icosi-dodecahedron.
it is possible to ascertain that:
The detailed examination, also by the
stereographic projection, of the reciprocal orientation of the rotation axes reveals that:
An important feature of the pair dodecahedron-icosahedron
is that they are duals: duality implies that in every dual pair the
two polyhedra interchange faces and vertices (including their number
and respective positions), whereas they
have the same number of edges, as follows from the known rule:
In this specific case, twelve faces and twenty vertices of the dodecahedron correspond
to twenty faces and twelve vertices of the icosahedron: therefore the edges are
thirty both
in the dodecahedron and in the icosahedron.
An important difference between icosahedral and crystallographic
point groups consists in the possibility that the indices usually assume the value
of irrational numbers, instead of being integers.
The dodecahedron, compatible with both icosahedral point groups, is the
unique form whose faces can be obtained from the twelve possible cyclic permutations, changes
of sign included, of just one set of three indices,
For example, eight of the twenty sets of three indices naming the faces of
the icosahedron are derived from

RHOMBIC TRIACONTAHEDRON AND ICOSIDODECAHEDRON
In addition to the 2-fold axes orthogonal to the faces, there
are also 3-fold and 5-fold axes passing through the vertices shared by three
or five faces, respectively; besides, pairs of orthogonal planes, parallel to
the diagonal of the rhombic faces, cross one another in correspondence of the
2-fold axes.
With reference to the five sets of three orthogonal 2-fold axes previously
described, the rhombic triacontahedron may be regarded as deriving from the
intersection of five cubes; the faces of each cube are orthogonal to one
of the five sets of three
2-fold axes. The five forms, related one another by the 5-fold axes and shown in
different colours in Fig.12, together with the 5-coloured rhombic
triacontahedron generated by their intersection, can be named:

The dual of the rhombic triacontahedron is the icosi-dodecahedron,
Archimedean polyhedron consisting of 20 triangular and 12 pentagonal faces,
orthogonal to 3-fold and 5-fold axes, respectively, whereas 2-fold axes pass
through the 30 vertices. Each vertex is shared by four polygons, namely a pair of
equilateral triangles and a pair of regular pentagons, oriented in an opposite
direction with respect to triangles and pentagons constituting the faces of
icosahedron and dodecahedron. In order to generate the
icosi-dodecahedron by the intersection of an icosahedron and a dodecahedron, the ratio between the
distances of their faces from the centre of the polyhedron must assume the following value:
![]()
and
the faces, placed at a unit central distance, that belong to the rhombic triacontahedron,
dual of the icosi-dodecahedron, result to be exactly tangent to the vertices of the
icosi-dodecahedron.
TRUNCATED ICOSAHEDRON AND PENTAKIS-DODECAHEDRON
![]()
ddodecahedron = 1.10
ddodecahedron = 1.05

ddodecahedron = 1
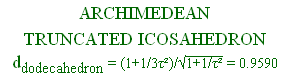
ddodecahedron = 0.921
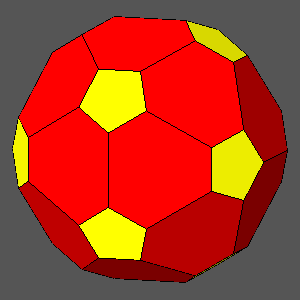
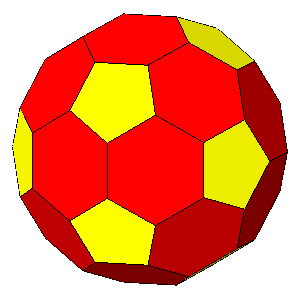
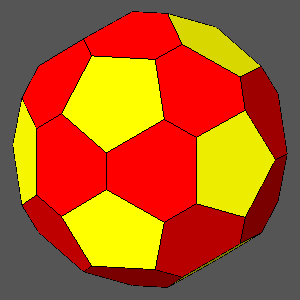
ddodecahedron = 0.9
ddodecahedron = 0.87
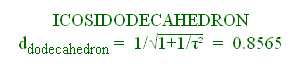



Whereas the central distance of the icosahedral faces is constant in every polyhedron and equal to
τ
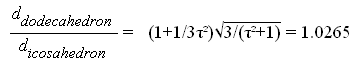
Each of its vertices is shared by three regular polygons, namely two hexagons and a pentagon.
Three- and five-fold axes are orthogonal to hexagonal and pentagonal faces, respectively,
whereas two-fold axes pass through the middle point of all the edges common to two hexagonal faces.
{1 3τ 0}, {τ3 τ 2},
{τ2+1 2τ 1}
If the height of the pyramids exceeds the value of Hmax, the polyhedron wouldn't be convex anymore.
_dodecahedron.png)
__pentakis-dodecahedron_1_2tau_0.png)
_pentakis-dodecahedron_dual.png)
_pentakis-dodecahedron_1_8tau_0.png)
_triacontahedron.png)
b) pentakis-dodecahedron
{1 2τ 0}
c) Catalan pentakis-dodecahedron {1 3τ 0}, dual of the Archimedean
truncated icosahedron, obtained when the height of the pyramids is
d) pentakis-dodecahedron {1 8τ 0}
e) rhombic triacontahedron {010}, obtained when the height of the pyramids is
Hmax= 0.425L.
dicosahedron = √3/τ = 1.0705dicosahedron = 1.05
dicosahedron = 1.03

dicosahedron = 1
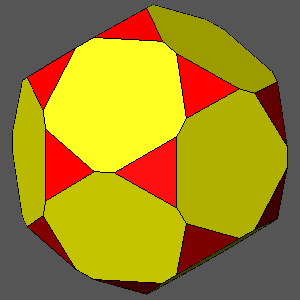
TRUNCATED DODECAHEDRON
dicosahedron = (τ /√3)(7τ-6)/5 = 0.9951dicosahedron = 0.97
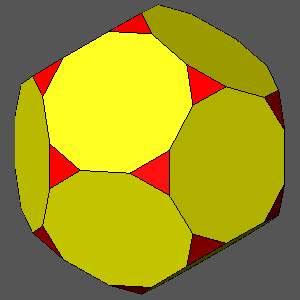
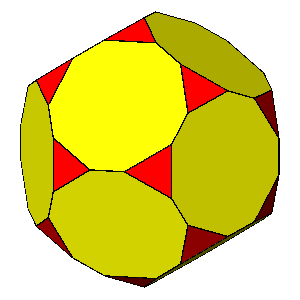
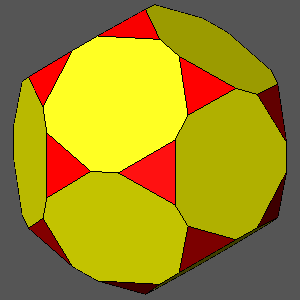
dicosahedron = 0.96
dicosahedron = 0.95
dicosahedron = τ /√3
= 0.93417


Whereas the central distance of the dodecahedral faces is constant in every polyhedron and equal to
1/√1+1/τ2,
the central distance of the icosahedral faces decreases from
√3/τ,
(at which value the faces of icosahedron are tangent to the vertices of dodecahedron), to
τ/√3, in case of
the icosi-dodecahedron; for such range of values, the faces of
a dual rhombic triacontahedron placed at a unit central distance would be tangent:
Three-fold and five-fold axes are orthogonal to triangular and decagonal faces
respectively, whereas two-fold axes pass through the middle of every edge common
to two decagonal faces.
The triangular faces of the pyramid (in which
the length of the two equal sides is 0.58L and the two equal angles
measure 30.48°) are 11.21°
inclined with respect to the base of the pyramid.
Also in this case, if the height of the pyramids exceeds the value of Hmax, the polyhedron wouldn't be convex anymore.
_triacontahedron.png)
_triakis-icosahedron_8tau_1_0.png)
_triakis-icosahedron_dual.png)
__triakis-icosahedron_2618_0618_0.png)
_icosahedron.png)
b) triakis-icosahedron {3τ2 1/τ 0}
c) Catalan triakis-icosahedron {τ2+1
1/τ 0}, dual of the
Archimedean truncated dodecahedron, obtained when the height of the pyramids is
d) triakis-icosahedron {τ2 1/τ 0}
e) icosahedron {τ 1/τ 0}, obtained in correspondence of the value Hmin=
0, meaning that the trigonal pyramids have flattened out completely.
Only in two circumstances, for particular values of the central distance
of the triacontahedrical faces, it happens that the decagons (rif:
polyhedron c) or the hexagons
(ref: polyhedron e) from non-regular
polygons become regular ones.
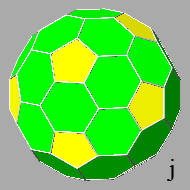
Proceeding with the truncation, before the complete elimination of the
icosahedral faces by the triacontahedral ones, in the resulting polyhedron there
is the simultaneous presence of triangular and pentagonal faces, both regular,
separated by octagonal faces of triacontahedron, which are
non-regular even though symmetric (ref: polyhedron h).
The length of the pair of longer sides decreases progressively as the further
truncation proceeds, arriving at the polyhedron
j, in which the lengths of all the sides of the hexagonal faces are
equal (the hexagons are not regular polygons, since the six angles between the sides of each hexagon assume two
different values).
Successively the hexagonal faces deform again, lengthening progressively
along a direction orthogonal to the direction along which they were stretched
previously
(ref: polyhedron k, in which the hexagonal faces consist of four short sides and two long sides), until the truncation eliminates also the pentagonal faces: at
this point the resulting polyhedron includes only the rhomb-triacontahedral faces (ref: polyhedron l).
Therefore no Archimedean polyhedron can be obtained just truncating an icosi-dodecahedron by means of a rhombic triacontahedron.


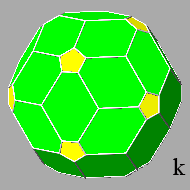
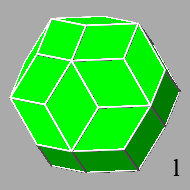






In fact, given a unit value to the central distance of the rhomb-triacontahedral
faces, if one denotes by:

ddodecahedron
= (1/√1+1/τ2)
(√3 dicosahedron
- 1/τ )
1/√1+1/τ2 < ddodecahedron < (3/τ2)/√1+1/τ2)
τ /√3 < dicosahedron < (1 +2/τ2) /√3
As one can see in Fig.24, all these polyhedra
include square triacontahedral faces that have increasing dimensions,
starting from the icosi-dodecahedron, where the square faces are absent, since the triacontahedron results exactly tangent to the vertices of the
icosi-dodecahedron, up to the rhombicosi-dodecahedron, where the
square faces reach the maximum dimension: the length of their side (equal to 2/τ3
if dtriacontahedron = 1) becomes equal to the length of the sides of the triangular and pentagonal faces.
ICOSIDODECAHEDRON |
dicosahedron = 0.94 | dicosahedron = 0.95 |
 |
 |
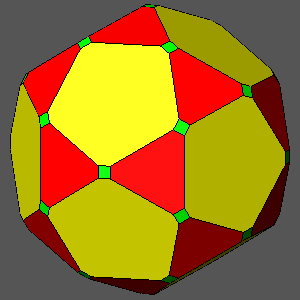 |
| dicosahedron = 0.97 | ARCHIMEDEAN TRUNCATED ICOSIDODECAHEDRON dicos = √3 /(1+ 2 /τ2) = 0.9819 |
dicosahedron = 0.99 |
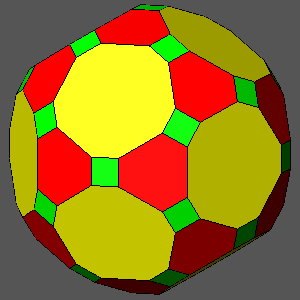 |
 |
 |
| dicosahedron = 1 | dicosahedron = 1.01 |
RHOMBICOSIDODECAHEDRON |
 |
 |
 |
|
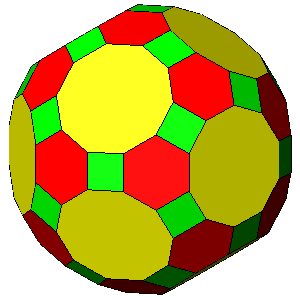
Fig.24 - Series of polyhedra, all characterized by square faces of triacontahedron,
included between two Archimedean semiregular polyhedra: the icosi-dodecahedron (left upper corner),
where the square faces are absent, being the triacontahedron tangent to the vertices of the icosi-dodecahedron,
and the rhombicosi-dodecahedron (right lower corner). In particular, hexagonal and decagonal faces are both regular
in the Archimedean truncated icosi-dodecahedron (in the centre of the figure). Whereas the central distance of the square faces of triacontahedron has always a unit value, the central distance of the dodecahedral faces can be obtained from the central distance of the icosahedral faces by the relation:
ddodecahedron
= (1/√1+1/τ2)
(√3 dicosahedron - 1/τ )
previously reported in the text. | ||
 |
 |
|
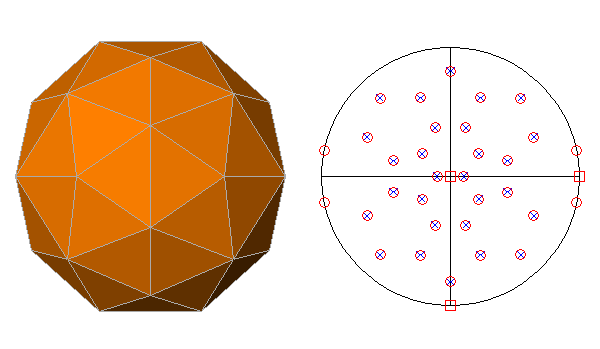
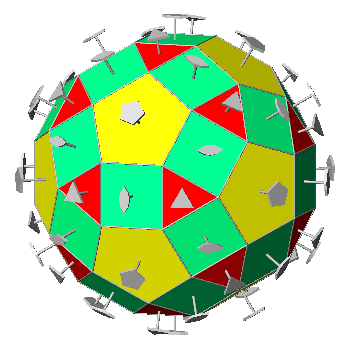
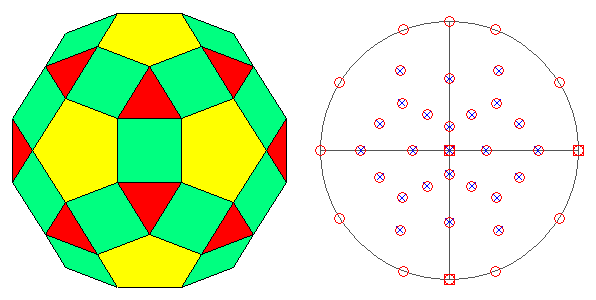
FIG.25 - Orthographic view of the rhombicosi-dodecahedron
(left) and its stereographic projection
(right), seen along the crystallographic axis c. | |
The polyhedron dual of the Archimedean rhombicosi-dodecahedron is the
Catalan deltoidal hexecontahedron,
(or deltoid-hexecontahedron), whose faces are named
by indices deriving from the cyclic permutations, changes of sign included, of the 3 sets of indices:
Therefore it consists of 12+24+24 = 60 faces having the shape of a deltoid (or kite), namely a quadrangle having two pairs of adjacent sides that are congruent.
A 3-fold axis and a 5-fold axis pass through the two vertices shared by
the couple of short sides and long sides, respectively,
whereas a 2-fold axis passes through each of the two other vertices of the face.
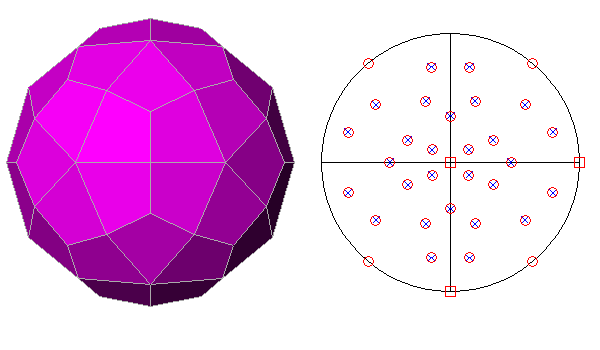
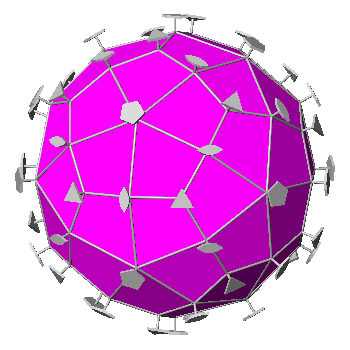 |
 |
|
FIG.26 - Orthographic view of the
Catalan deltoidal hexecontahedron (left), dual of the rhombicosi-dodecahedron, and its stereographic projection
(right), seen along the crystallographic axis c. | |
The (1+1/τ2 1 0) face of the
Catalan deltoidal hexecontahedron makes an angle of
14.98° with the (τ 1/τ 0) face of the icosahedron and an angle of 22.39° with
the (1τ 0) face of the dodecahedron.
The corresponding face in every other generic deltoidal
hexecontahedron has indices (hk0) such that
_icosahedron.png) |
_deltoidal-hexecontahedron_210.png) |
_deltoidal-hexecontahedron_dual.png) |
_deltoidal-hexecontahedron_110.png) |
_dodecahedron.png) |
|
a) icosahedron
{τ 1/τ 0} b) deltoidal hexecontahedron {210} c) Catalan deltoidal hexecontahedron {τ+1/τ τ 0} dual of the Archimedean rhombicosi-dodecahedron d) deltoidal hexecontahedron {110} e) dodecahedron {1τ 0} | ||||
DODECAHEDRON |
dicosahedron = (1+4/τ7) τ /√3 | dicosahedron = (1+1/2τ3) τ /√3 |
|
|
|
|
| dicosahedron = (1+2/τ6) (τ /√3) | RHOMBICOSI-DODECAHEDRON dicos. = (1+ 2 / τ2)/√3 = (1+1/τ5) τ /√3 ddod. = 3/τ2√1+1/τ2 = (1+1/τ4)/√1+1/τ2 |
dicosahedron = (1+2/τ7) τ /√3 |
|
|
|
|
| dicosahedron = (1+1/τ6) τ /√3 | dicosahedron = (1+1/τ7) τ /√3 | ICOSAHEDRON dicosahedron = τ /√3 ddodecahedron = √1+1/τ2 |
|
|
|
|
|
FIG.28 - Series of polyhedra, dual both of
Catalan and generic deltoidal hexacontahedra, describing the transformation of dodecahedron into icosahedron
passing through an Archimedean polyhedron, the rhombicosi-dodecahedron;
in every intermediate polyhedron all the vertices are shared by four polygons:
a pentagon, a triangle and two rectangles becoming squares only in the rhombicosi-dodecahedron.
For every intermediate polyhedron, given a unit value to the central distance of the triacontahedral faces, the distance of the dodecahedral faces can be obtained, starting from the reported distance of the icosahedral faces, by the relation: ddodecahedron
= (1/√1+1/τ2)
(4 -√3τ
dicosahedron) | ||
Concerning the dual pair formed by the Catalan deltoidal hexecontahedron and the Archimedean rhombicosi-dodecahedron (and more in general the pairs made of a generic deltoidal hexecontahedron and its dual), the total number of faces and vertices corresponds to:
Consequently the edges are 120 in
each polyhedron of the pair.
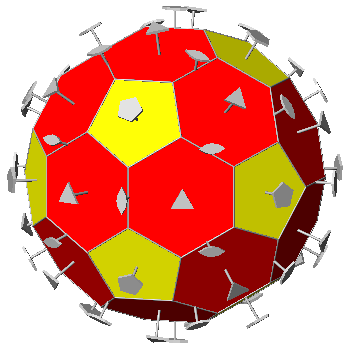
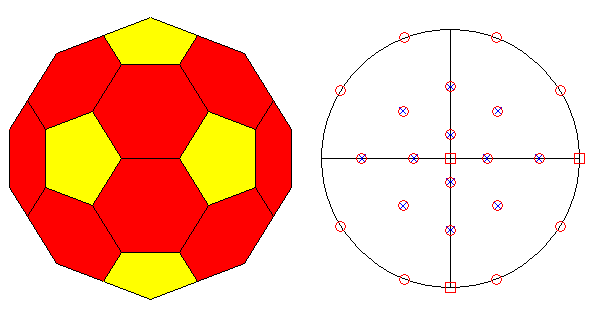
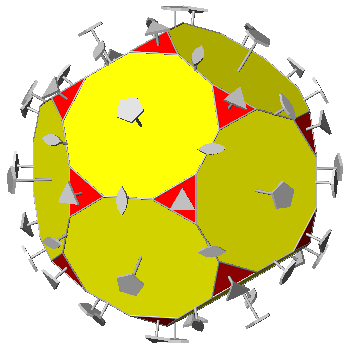
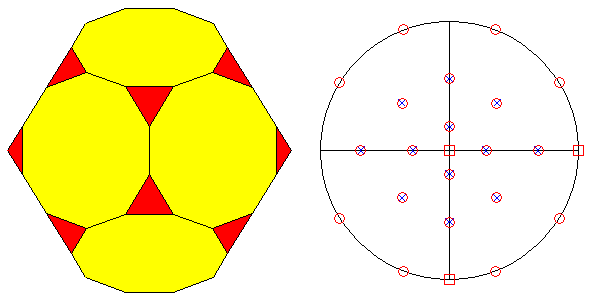
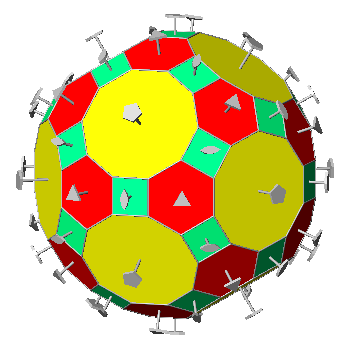
TRUNCATED ICOSI-DODECAHEDRON AND HEXAKIS-ICOSAHEDRON
In the Archimedean truncated
icosi-dodecahedron, consisting of
twelve decagonal faces of dodecahedron, twenty hexagonal faces of icosahedron and thirty square faces of triacontahedron, each vertex
is shared by three polygons: a regular decagon, a regular
hexagon and a square. As regards the axes of rotation,
 |
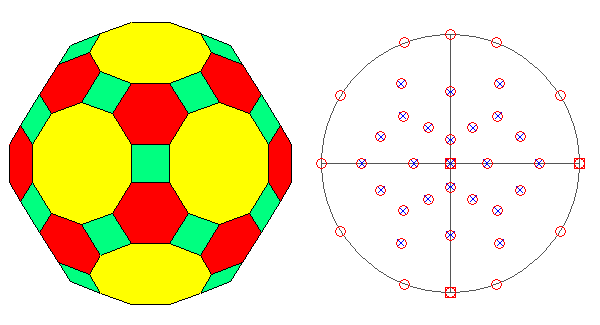 |
FIG.29 -
Orthographic view of the Archimedean truncated icosi-dodecahedron (left) and its stereographic projection
(right), seen along the crystallographic axis c. | |
The polyhedron dual of the Archimedean truncated icosi-dodecahedron is the hexakis-icosahedron (named also dis-dyakis-triacontahedron
and decakis-dodecahedron),
Catalan polyhedron whose faces are named by indices deriving, in this instance, from the cyclic
permutations, changes of sign included, of the following five sets of indices:
{τ+2/τ 1/τ2 1/τ2}, {τ2 1 2/τ2}, {2+1/τ2 τ 1/τ2}, {2 3/τ 1}, {τ+1/τ 2/τ 1+1/τ2}
Consequently the hexakis-icosahedron consists of 5x24 = 120 faces, having the
shape of a scalene triangle (rather similar to a right-angled triangle), whose
angles measure 88.99°, 58.24°, 32.77°; differently from all the aforementioned
icosahedral polyhedra, it
does not include any face with an index equal to zero, namely parallel to a
2-fold axis, being in a general position with respect to every symmetry operator.
The ratios between the lengths of the sides of every triangular face have the following values:
| L1 /L2 = 2(5-2τ)/3 = 1.1759 | L2 /L3 = 3τ2/5 = 1.5708 | L1 /L3 = 2(τ+3)/5 = 1.8472 |
In case of the pair of dual polyhedra formed by the Catalan hexakis-icosahedron and the Archimedean truncated icosidodecahedron, the total number of faces and vertices is:
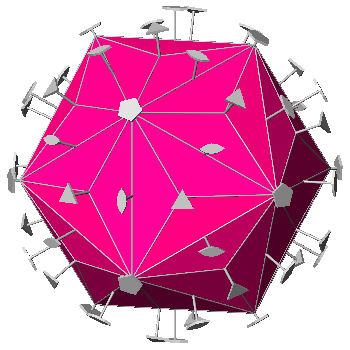
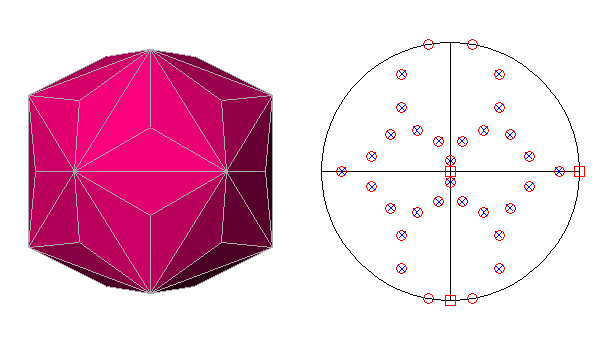
PENTAGONAL HEXECONTAHEDRON AND SNUB DODECAHEDRON
 |

|
|
FIG.31 -
Comparison between an asymmetric pentagonal
face and the symmetric one belonging to the pentagonal hexecontahedron, dual of the snub dodecahedron. As described in the text, an asymmetric pentagonal face belongs also to the particular pentagonal hexecontahedron whose intersection with icosahedron and dodecahedron gives rise to a snub dodecahedron when the ratio between: and |
Even though the polyhedron is chiral, therefore lacking mirror planes on the whole,
for a particular orientation of the faces it happens that each face
of the pentagonal hexecontahedron is locally symmetric with respect to a mirror plane.
As a consequence of the fact that in such a case also the fifth side has the same length of the
pair of short sides, four of the angles of the pentagonal faces are equal (118.14°),
whereas the fifth angle, the one between the couple of longest sides, is smaller than the others and measures 67.44°.
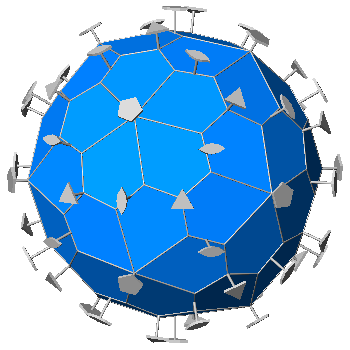 |
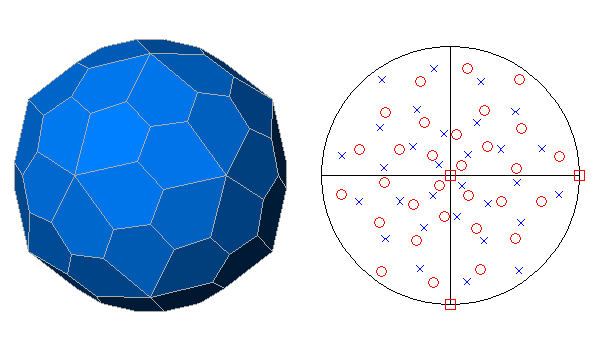 |
FIG.32- Orthographic view of the pentagonal hexecontahedron (left), dual of the snub-dodecahedron, and its stereographic projection
(right), seen along the crystallographic axis c. | |
The Archimedean polyhedron dual of this particular pentagonal hexecontahedron is the snub dodecahedron; it consists in the intersection of three forms :
The orientation, with respect to the crystallographic reference axes, of the faces (having the shape of an irregular pentagon) that belong to this pentagonal
In the snub dodecahedron the faces deriving from the
icosahedron and the pentagonal hexecontahedron have the same central
distance: the value of its ratio with respect to the central distance of
the dodecahedral faces is 1.0486.
This geometrical configuration generates the 92 faces of
the snub dodecahedron, all having the shape of regular polyhedra:
in detail, twelve pentagons and eighty triangles. The twelve pentagons and twenty
out of the eighty triangles obviously come from the dodecahedron and the icosahedron,
respectively, whereas the other sixty triangles come from the
pentagonal hexecontrahedron, whose irregular pentagonal faces are drastically
modified by the simultaneous intersections with dodecahedral and icosahedral
faces.
Since for the dual pair snub dodecahedron-pentagonal hexecontahedron: F+V = 92+60 = 152, both polyhedra have 150 edges.
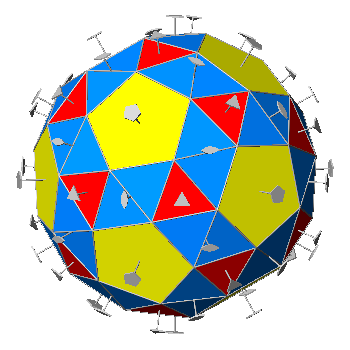 |
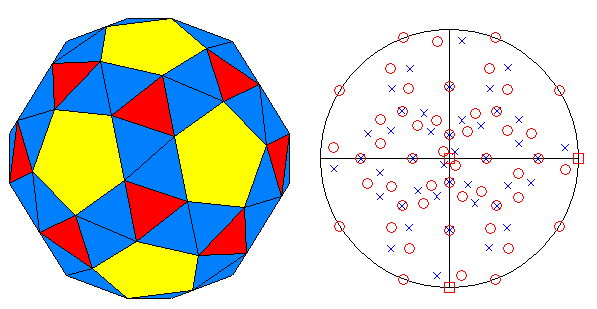 |
FIG.34 - Orthographic view of the snub-dodecahedron (left) and its stereographic projection
(right), seen along the crystallographic axis c. | |
The positions of the rotation axes, with respect to the single forms constituting the snub dodecahedron, are the following:
Each pentagonal face of the dodecahedron shares its five vertices with as many
triangular faces of the icosahedron, whereas each triangular face of the
icosahedron shares its three vertices with as many pentagonal faces of the
dodecahedron.
On the whole, each vertex of the snub dodecahedron is shared among five faces, a pentagonal
face and four equilateral triangular ones: three of these triangular faces derive from the
pentagonal hexecontahedron and one from the icosahedron.
As a valid alternative to snub dodecahedron, the name of snub icosidodecahedron has been proposed
for this polyhedron, since both the pentagonal
faces of the dodecahedron and the triangular faces of the icosahedron share each side with
one side of a triangular face deriving from the pentagonal hexecontahedron, by which
therefore they are bordered.
In turn, each triangular face derived from the
pentagonal hexecontahedron shares one of its sides with a pentagonal face of
the dodecahedron and a second side with a triangular face of the icosahedron, whereas the third side is in
common with another triangular face, coming from the pentagonal hexecontahedron,
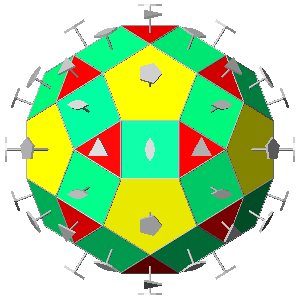
with which it makes a pair. Since in the snub dodecahedron there
are in total thirty pairs of these triangular faces, one can describe the snub
dodecahedron as a distortion of the rhombicosidodecahedron (Fig.35),
assuming that the pair
of triangular equilateral faces derived from the pentagonal
hexecontahedron replaces each square face of the
triacontahedron, with a consequent rotation of the twelve pentagonal faces and
the other twenty triangular faces around the 5-fold and 3-fold rotation axes orthogonal to
every face.
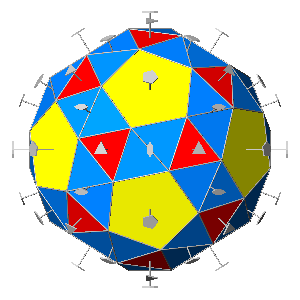
|
 |
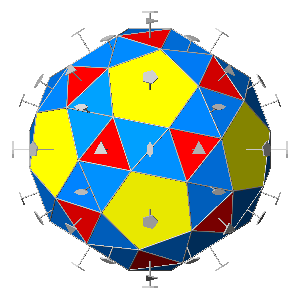 |
| FIG.35 - Comparison between the rhombicosidodecahedron
and the pair of chiral snub-dodecahedra (viewed along the crystallographic | ||
As alredy pointed out, there are chiral forms for both the pentagonal hexecontahedron and its dual, the snub dodecahedron; in Fig.36 each row shows the chiral pairs, each column the dual pairs.
In Fig.37 one can see some peculiar forms, consisting in the intersection (for appropriate values of the central distances of the faces) of the dual pairs made of an Archimedean polyhedron and the corresponding Catalan polyhedron.
icosidodecahedron&rhombic-triacontahedron.png) |
truncated_dodecahedron&tria_kis_icosahedron.png) |
truncated_%20icosahedron&pentakisdodecahedron.png) |
| icosidodecahedron & dual rhombic triacontahedron |
truncated dodecahedron & dual triakis-icosahedron |
truncated icosahedron & dual pentakis-dodecahedron |
rhomb-triaconta_icosidodecahedron&deltoid-hexecontahedron.png) |
truncated_icosidodecahedron&hexakisicosahedron.png) |
snub_dodecahedron&pentagon-hexecontahedron.png) |
|
rhombicosidodecahedron |
truncated icosidodecahedron |
snub dodecahedron |
|
FIG.37 - Rounded icosahedral forms deriving from the intersection of the
dual pairs made of an Archimedean semiregular polyhedron and the corresponding
Catalan polyhedron: they all have the peculiarity
(deriving from the assignation of appropriate values to the central distances of the faces) that each vertex is
shared by two faces belonging to the Archimedean solid and two faces of the dual Catalan solid. | ||
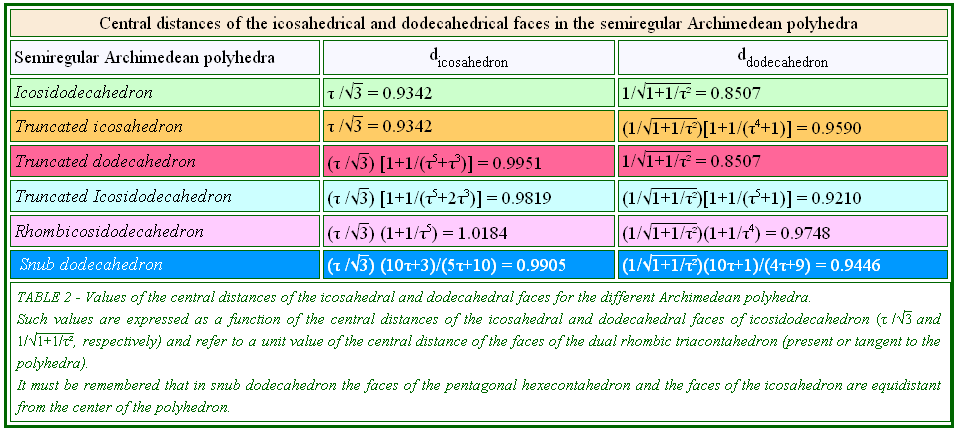
In the first of the following summarizing Tables, the central
distances of the icosahedral and dodecahedral faces belonging to semiregular
Archimedean polyhedra are reported.
In the next Table, one can find the shapes assumed by the faces of Catalan
polyhedra, dual of semiregular Archimedean polyhedra, and the relative
geometric parameters (L indicates the length of the sides of the
polygons).
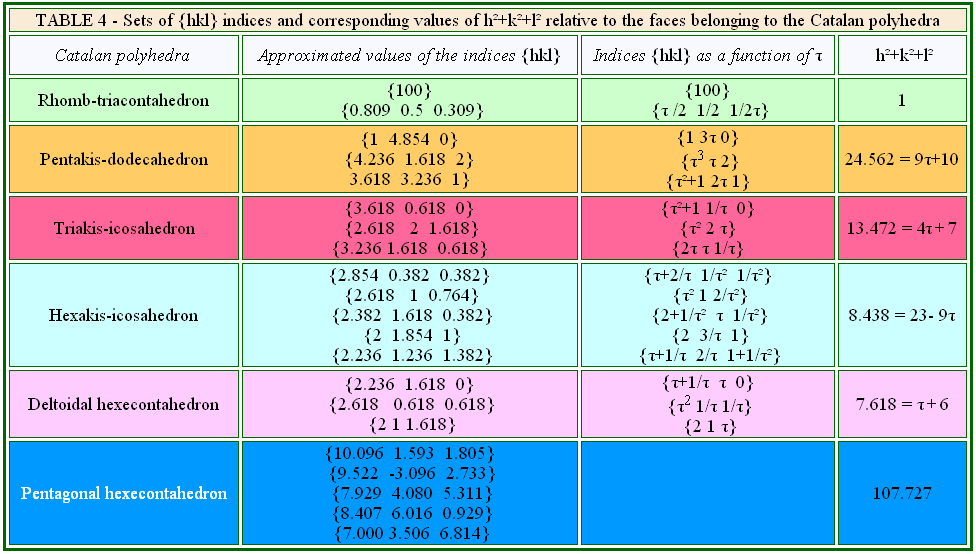
In the last Table, the sets of {hkl} indices characterizing the Catalan polyhedra are reported together with
the corresponding values of the sum: h2+k2+l2. Taking into account that
the root of such sums is proportional to the reciprocal central distance dhkl of
a (hkl) face, the sum h2+k2+l2
must be constant for
the set of indices of each Catalan polyhedron, since all its faces have the same central distance.

For instance, the faces of the rhomb-triacontahedron derive from two different kinds of indices, written as:
The values, given in the present work, of both the indices of the faces and the
central distances of the polyhedra have been obtained by means of a
procedure that will be described in a next publication.
The icosahedral forms having a particular importance are the
ones with
minor multiplicity, namely dodecahedron, icosahedron and rhomb-triacontahedron.
As already seen, it is from their intersection (analogously to what
happens in the cubic system for the three forms: cube, octahedron and rhomb-dodecahedron), that the Archimedean polyhedra with icosahedral symmetry can be
generated (except the snub dodecahedron, since it includes also the pentagonal
hexecontahedron), attributing appropriate values to the respective central distances.
The duals of these isogonal Archimedean polyhedra are the isohedral Catalan polyhedra characterizing the icosahedral symmetry (or the cubic symmetry, regarding the
other Catalan polyhedra, dual of Archimedean polyhedra which derive from the
intersection of cube, octahedron and rhomb-dodecahedron).
The rounded polyhedron shown in Fig.38 results from the intersection of
all the seven forms belonging to the m35
point group (two Platonic polyhedra, the dodecahedron and the icosahedron, and five Catalan polyhedra),
in the particular event that the central distances of all the faces are equal.
|
|
|
FIG. 39 -
View along the crystallographic axis c and stereographic projection of
the rounded composite polyhedron made of the seven single forms belonging to the m35 point group
and having all the same central distance, which coincide with the Catalan and
Platonic solids. |
Starting from the truncated icosidodecahedron, in Fig.40 each dodecahedral, icosahedral and triacontahedral face is progressively substituted, through an "augmentation" process, by a decagonal, hexagonal and square pyramid, respectively. Each pyramid is made of pairs of faces, symmetrically orientated with respect to the rotation axes, belonging to two polyhedra out of the set of three: triakis-icosahedron, pentakis-dodecahedron and deltoidal hexecontahedron.
 | |
|
FIG. 40 - Progressive substitution of each face of a truncated icosidodecahedron with
pyramids made of pairs of faces,
coming from the set of three polyhedra: triakis-icosahedron,
pentakis-dodecahedron and deltoidal hexecontahedron, placed
in symmetric position with respect to the 2-fold, 3-fold and 5-fold rotation
axes. | |
In general, all the polyhedra having icosahedral symmetry can be considered to derive from
the intersection of whichever number of forms (each of them made of faces at a
different central distance), belonging to two different sets:


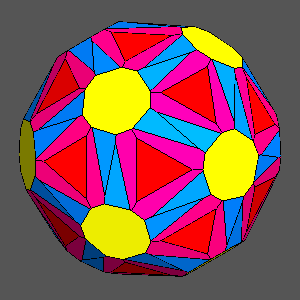
235 and m35 point groups:
m35 point group:
235 point group:
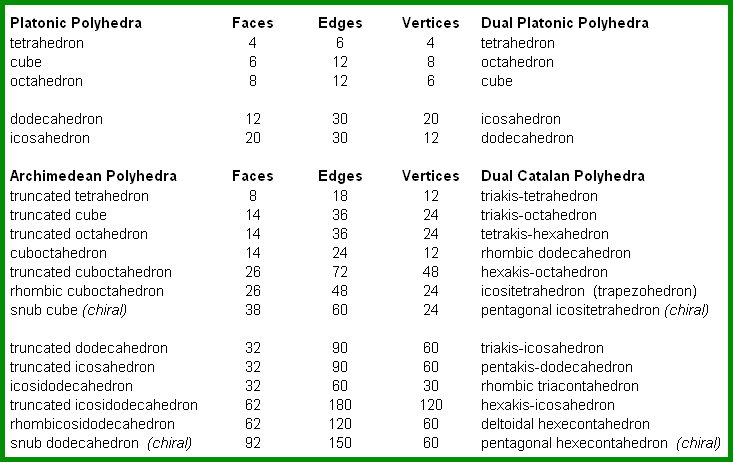
The number of faces, edges and vertices relative to all the regular Platonic and semiregular Archimedean polyhedra
is
reported in Table 5; the number of faces and vertices is obviously interchanged
in their duals (Platonic and Catalan polyhedra, respectively),
whereas the number of edges holds steady. In conclusion, it is
noteworthy to point out that, by an identical procedure, one can describe the
other Platonic and
Archimedean polyhedra, as well as their dual Catalan polyhedra, characterized
by a cubic symmetry, and consequently all the possible forms deriving
from their combination.
Many thanks are due to Fabio Somenzi for his precious help concerning the translation of the text.
Canadian Mineralogist, vol.14, 567-570 (1976)
[2] Rigault G. - Sul gruppo puntuale 235
Estratti dagli "Atti dell'Accademia delle Scienze di Torino", vol. 117(1983)
[3] Loreto L., Farinato R., Pappalardo F.
- Icosahedral Symmetry, Icosahedral Polyhedra and Indexing methods
in
"Topics on contemporary
crystallography and quasicrystals", special Issue of "Periodico di Mineralogia"
Vol. LIX (1990) - L. Loreto
and M. Ronchetti Editors
[4] Cahn J.W. & Gratias D. - Indexing of Icosahedral Quasiperiodic Crystals
J. Mater. Res., vol.1, 13-26 (1986)
[5] Hahn T. & Klapper K. - Non crystallographic point group
in "International Tables for Crystallography", Volume A: Space-Group Symmetry, 796 (2005) - Theo Hahn Editor
[6] Weissbach B. & Martini H. - On the Chiral Archimedean Solids
Contribution to Algebra and Geometry, vol.43,
No.1, 121-133 (2002)