Vertex- and edge-truncation of the Platonic and Archimedean solids leading to vertex-transitive polyhedra
Livio Zefiro*
*Dip.Te.Ris, Universita' di Genova, Italy
(E-mail address:
livio.zefiro@fastwebnet.it)
Notes
|

|
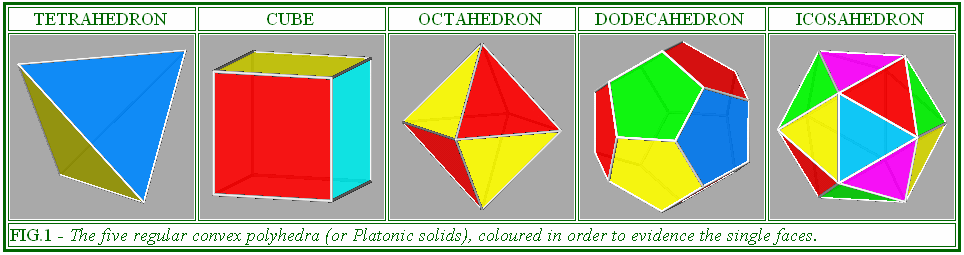
ARCHIMEDEAN TRUNCATED CUBE | ARCHIMEDEAN TRUNCATED DODECAHEDRON |
|
|
 |
doctahedron /dcube= (√2+1)/√3 = 1.3938 |
ddodecahedron /dicosahedron = √3(τ2+1)/(3τ-1) = 0.8548 |
|
CUBOCTAHEDRON |
ICOSI-DODECAHEDRON |
|
|
|
doctahedron /dcube= 2/√3 = 1.1547 |
ddodecahedron /dicosahedron = √3/√τ2 +1 = 0.9106 |
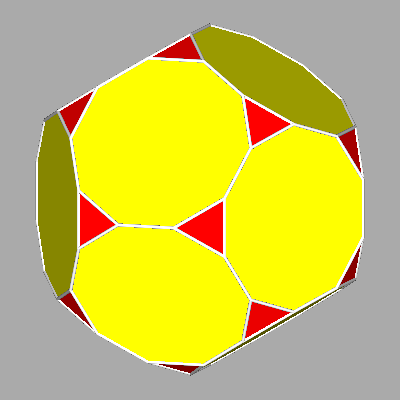
| ARCHIMEDEAN TRUNCATED OCTAHEDRON | ARCHIMEDEAN TRUNCATED ICOSAHEDRON |
 |
 |
doctahedron /dcube= √3/2 = 0.8660 |
ddodecahedron /dicosahedron = (3+1/τ2)/√3(τ2+1) = 1.0265 |
|
FIG.2- Archimedean polyhedra resulting from the intersection between the two couples of dual solids consisting of cube and octahedron (left column) and dodecahedron and icosahedron (right column). |
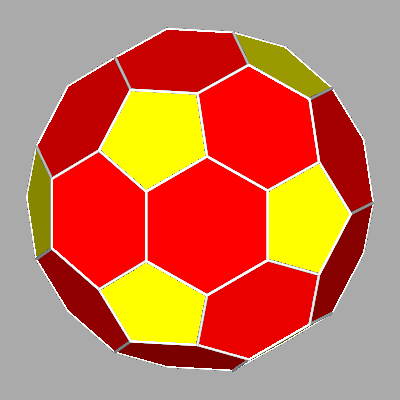
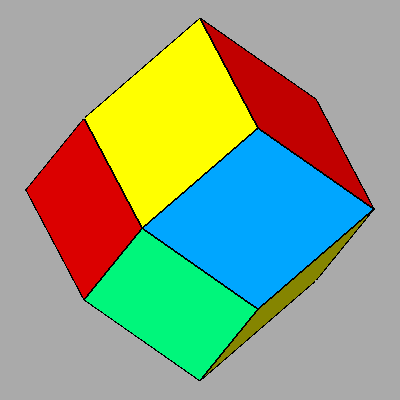
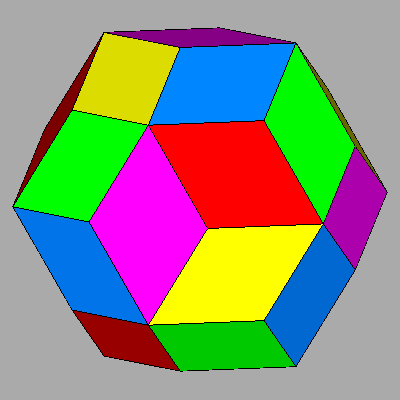
| RHOMB-DODECAHEDRON | RHOMB-TRIACONTAHEDRON |
 |
 |
|
FIG.3- Rhomb-dodecahedron (left) and rhomb-triacontahedron (right), Catalan duals of the Archimedean cuboctahedron and icosi-dodecahedron respectively | |
|
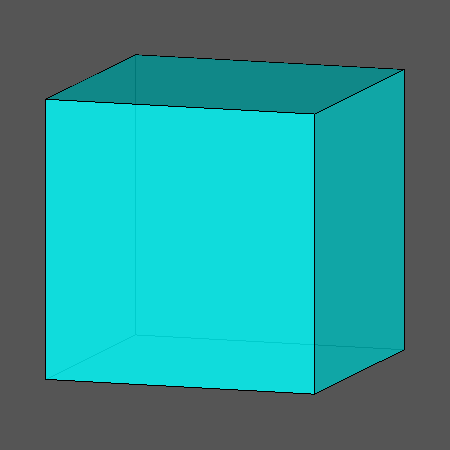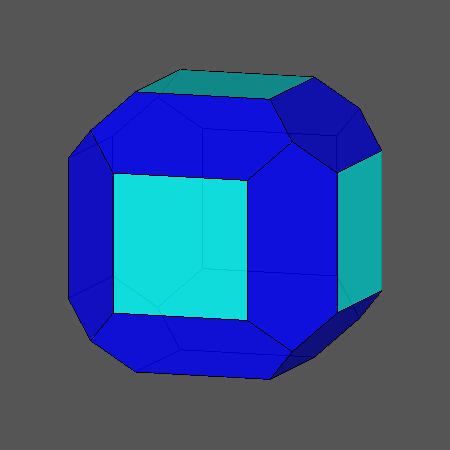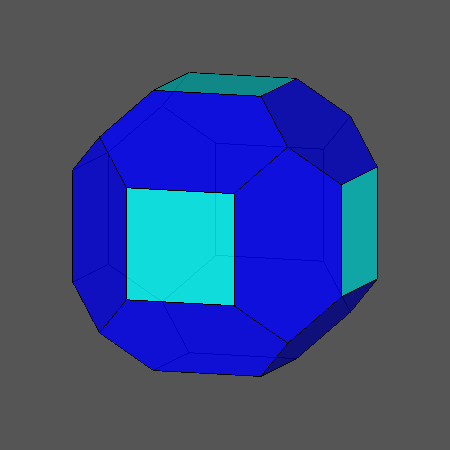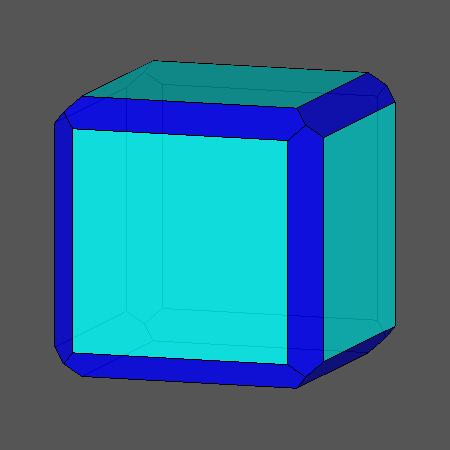
Edge-truncation of cube and octahedron by a rhomb-dodecahedron |
|
 |
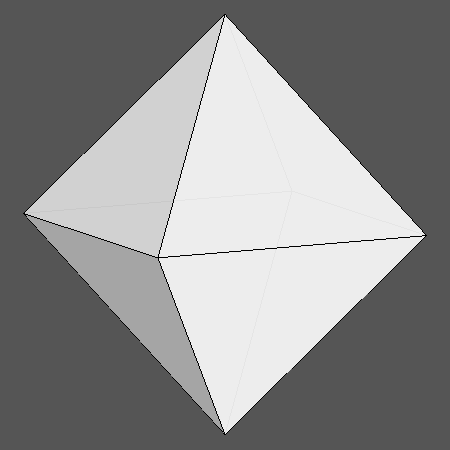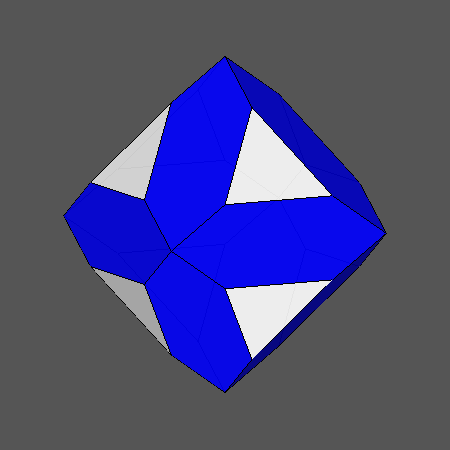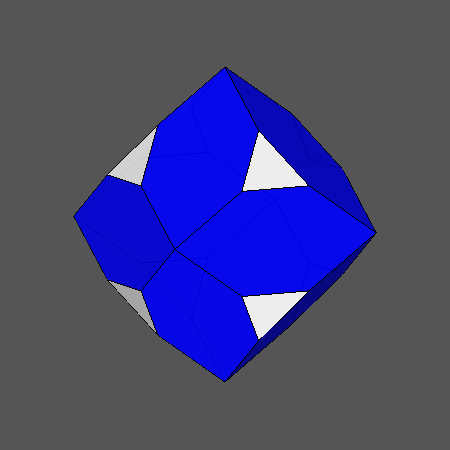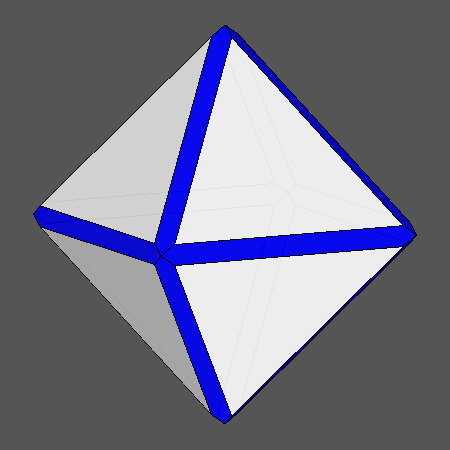 |
|
FIG.4a- Sequences of the edge-truncation by a rhomb-dodecahedron of a cube (left) and an octahedron (right) | |
|
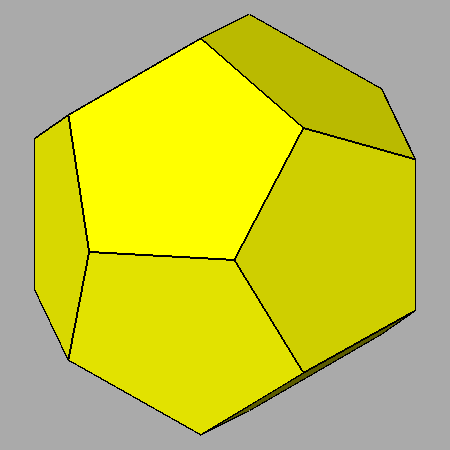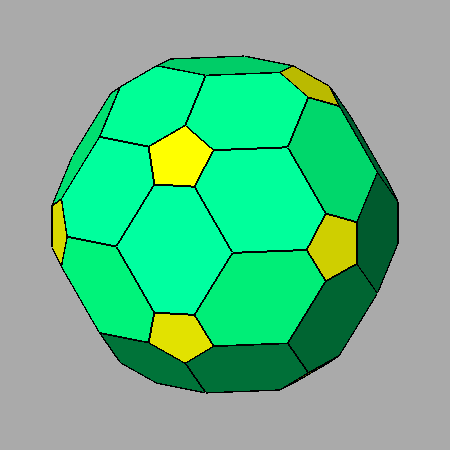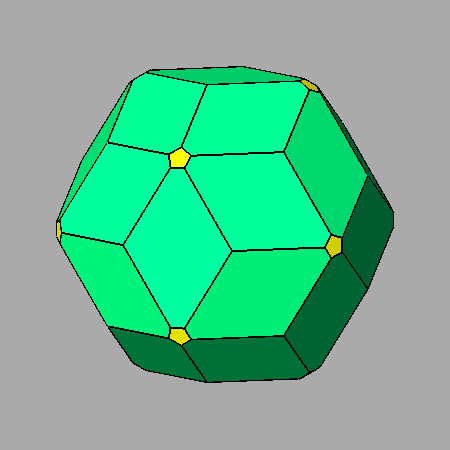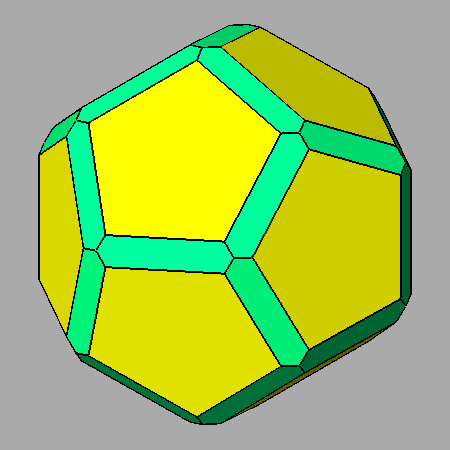
Edge-truncation of dodecahedron and icosahedron by a rhomb-triacontahedron |
|
 |
 |
|
FIG.4b- Sequences of the edge-truncation by a rhomb-triacontahedron of a dodecahedron (left) and an icosahedron (right) | |
 |
 |
 |
|
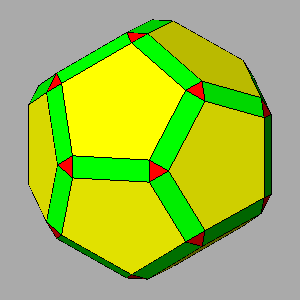
edge-truncation |
vertex-truncation
|
edge-truncation
|
 |
 |
 |
|
edge-truncation |
vertex-truncation |
edge-truncation |
|
FIG.5- Vertex-transitive polyhedra, duals of deltoid-icositetrahedra or deltoid-hexecontahedra, resulting from the intersection of cubic or icosahedral Archimedean polyhedra with the rhomb-dodecahedron (upper row) or the rhomb-triacontahedron (lower row). | ||
|
COMPOSITE POLYHEDRA RESULTING FROM THE VERTEX-TRUNCATION OF AN ARCHIMEDEAN SOLID BY ITS CATALAN DUAL |
| TRUNCATED CUBE and TRIAKIS-OCTAHEDRON | TRUNCATED DODECAHEDRON and TRIAKIS-ICOSAHEDRON |
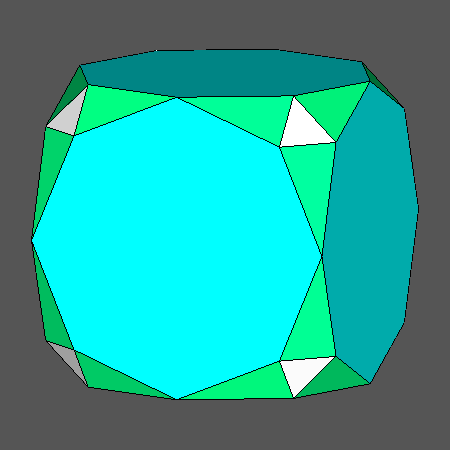
|
|
|
FIG.6a-
Intersections between couples of dual Archimedean and Catalan
polyhedra consisting in:
| |
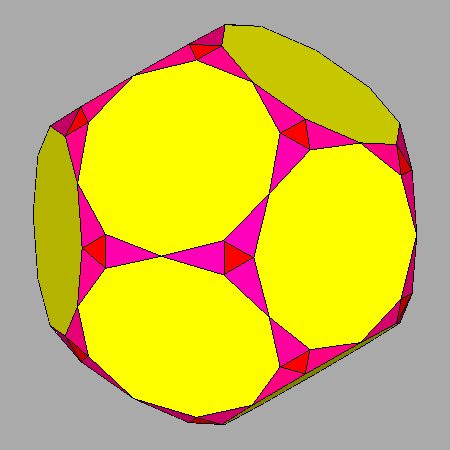
| TRUNCATED OCTAHEDRON and TETRAKIS-CUBE |
TRUNCATED
ICOSAHEDRON and PENTAKIS-DODECAHEDRON |
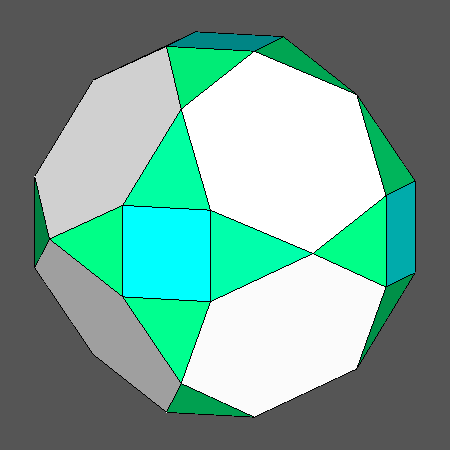 |
|
|
FIG.6b-
Intersections between couples of
dual Archimedean and Catalan polyhedra consisting in: | |
|
Sequence of vertex-truncations of the cuboctahedron
by a rhomb-dodecahedron |
||
_CO_.png) |
_CO_R_0.9_.png) |
_CO_R_0.8536_.png) |
The faces of the rhomb-dodecahedron are tangent to the twelve vertices of the cuboctahedron |
drhomb-dodecahedron = 0.9 |
The faces deriving from the cube have the shape of a regular octagon |
_CO_R_0.833_.png) |
_CO_R_0.8_.png) |
_CO_R_0.75_.png) |
|
The faces deriving from the octahedron have the shape of a regular hexagon |
drhomb-dodecahedron = 3/4 Each vertex is shared among four faces |
|
_CO_R_0.72_.png) |
_CO_R_0.6_.png) |
_CO_R_0.5_.png) |
|
drhomb-dodecahedron = 0.72 |
drhomb-dodecahedron = 0.6
Vanishing of the faces of octahedron |
drhomb-dodecahedron = 1/2
The only faces of rhomb-dodecahedron survive
|
|
FIG.7a- Sequence of the complete vertex-truncation by rhomb-dodecahedron of cuboctahedron: only the forms of the first two rows are vertex-transitive. | ||
The completely analogous sequence relative to the
truncation of the icosi-dodecahedron by a rhomb-triacontahedron is shown in Fig.7b.
The face transitive duals of the series of vertex-transitive polyhedra go from
the rhomb-triacontahedron to the deltoid-hexecontahedron {τ10}, passing
through a continuous series of intermediate hexakis-icosahedra (also called disdyakis-triacontahedra).
|
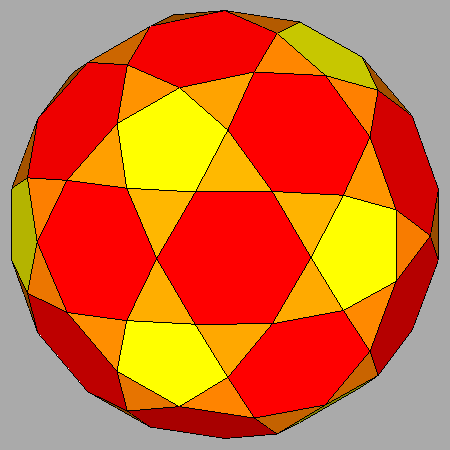
Sequence of vertex-truncations of the icosi-dodecahedron by
a rhomb-triacontahedron (RT) |
||
 |
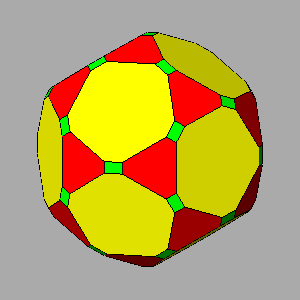 |
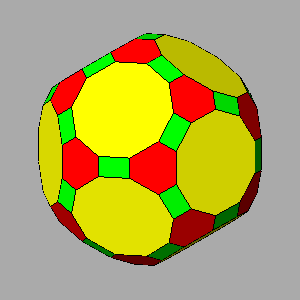 |
The faces of rhomb-triacontahedron are tangent to the thirty vertices of
the icosi-dodecahedron |
dRT = 0.97 |
The faces of dodecahedron assume the shape of a regular decagon |
 |
 |
 |
|
The faces of icosahedron have the shape of a regular hexagon |
dRT
= (τ2+1)/4 = 0.9045
|
|
 |
 |
 |
|
dRT = 0.89 |
dRT = τ2/3 = 0.8727 |
dRT = 1/(1+1/τ2)= 0.7236 The only faces of rhomb-triacontahedron |
|
FIG.7b- Sequence of the complete vertex-truncation of the icosi-dodecahedron by a rhomb-triacontahedron: only the forms reported in the first two rows are vertex-transitive. | ||
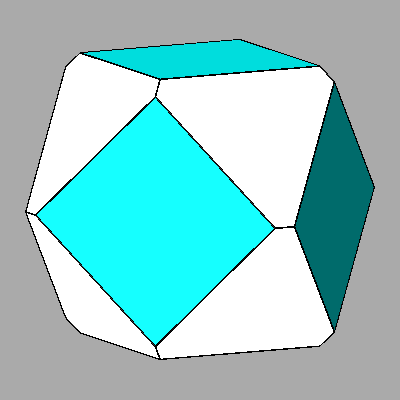
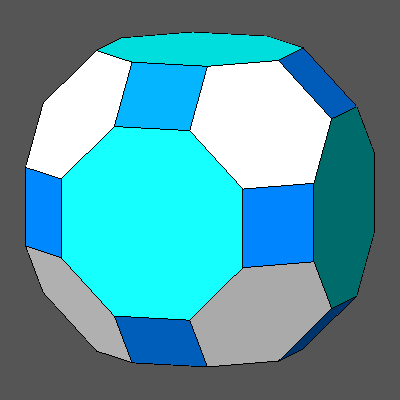
doctahedron /dcube= √3/(3-√2) = 1.0922 |
doctahedron /dcube
= 1.0922 dcube /drhomb-dodecahedron = 0.8673 doctahedron /drhomb-dodecahedron = 0.9473 |
 |
 |
|
FIG. 8a - The edge-truncation by a rhomb-dodecahedron of a non Archimedean truncated octahedron leads to the Archimedean truncated cuboctahedron when the ratio doctahedron / dcube= √3/(3-√2). | |
ddodecahedron /dicosahedron = √(3-τ)3/3 = 0.9380 |
d dodecahedron /dicosahedron = 0.9380dicosahedron /drhomb-triacontahedron = 0.9819 ddodecahedron /drhomb-triacontahedron = 0.9210 |
 |
 |
|
FIG.8b - The edge-truncation of a non Archimedean truncated icosahedron by a rhomb-triacontahedron leads to the Archimedean truncated icosidodecahedron when the ratio ddodecahedron / dicosahedron = √(3-τ)3/3. | |
Analogously, in Fig. 9a and Fig. 9b one can see how the Archimedean
rhomb-cuboctahedron and
rhomb-icosidodecahedron derive from the
edge-truncation of two other non-Archimedean polyhedra, a truncated octahedron and a
truncated icosahedron, both slightly different from the previous ones shown in
Fig.
8a and Fig. 8b.
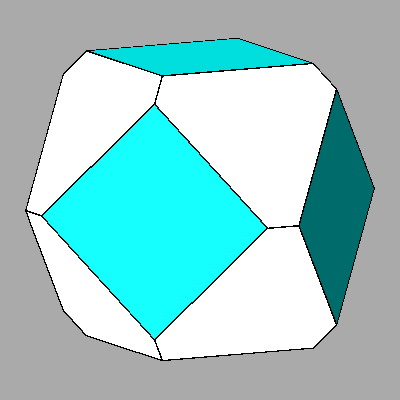
doctahedron /dcube = (2√2 -1)/√3 = 1.0556 |
doctahedron /dcube
= 1.0556 dcube /drhomb-dodecahedron = 1.0 doctahedron /drhomb-dodecahedron = 1.0556 |
 |
 |
|
FIG. 9a - Edge-truncation by a rhomb-dodecahedron of a non-Archimedean truncated octahedron, slightly different from the previous one (ratio doctahedron / dcube = 1.0556), leading to the rhomb-cuboctahedron. | |
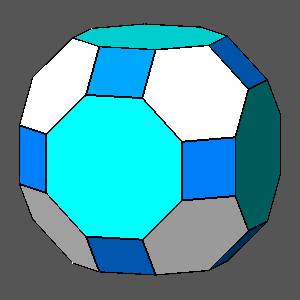
| ddodecahedron/dicosahedron = 3√3 / [(3+τ)√3-τ] = 0.9571 |
ddodecahedron /dicosahedron= 0.9571 |
 |
 |
|
FIG. 9b - Edge-truncation by a rhomb-triacontahedron of a non-Archimedean truncated icosahedron, slightly different from the previous one (ratio ddodecahedron /dicosahedron = 0.9571), leading to the rhomb-icosidodecahedron. | |
 |
 |
 |
|
Archimedean
|
truncation
by rhomb-dodecahedron |
Archimedean rhomb-cuboctahedron |
 |
 |
 |
|
Archimedean |
truncation by
rhomb-triacontahedron |
Archimedean |
|
FIG. 10- The further truncation of both Archimedean truncated cuboctahedron and truncated icosidodecahedron (on the left) leads to the vertex-transitive polyhedra shown in the central images, which can be compared with the isomorphic rhomb-cuboctahedron and rhomb-icosidodecahedron (on the right). | ||
| tC | CO | tO | tCO | RCO |
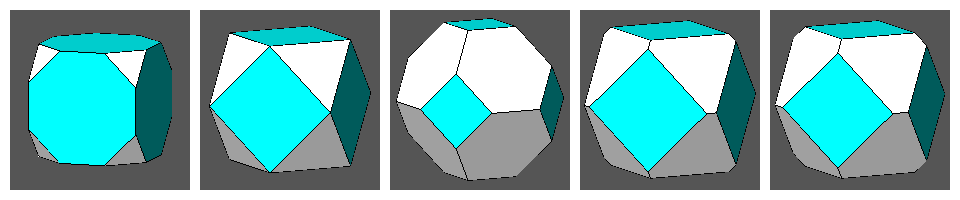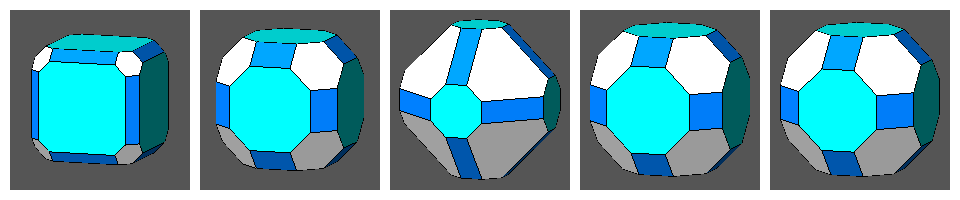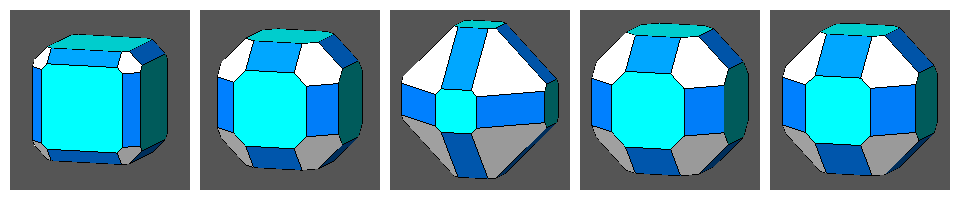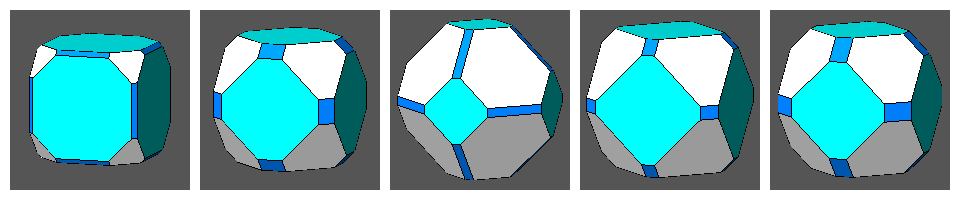 | ||||
|
FIG. 11 -
Sequences of vertex-transitive polyhedra deriving from the truncation by a rhomb-dodecahedron of:
A further decrease of the central distance of the intersecting rhomb-dodecahedron transforms the Archimedean truncated cuboctahedron in a vertex transitive polyhedron whose dual, analogously to the other four cases, is a face-transitive deltoid-icositetrahedron. |
||||
| tD | ID | tI | tID | RID |
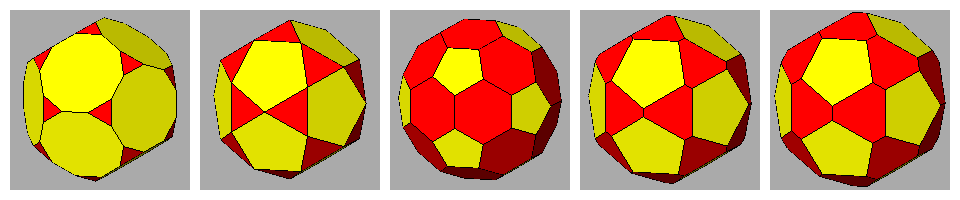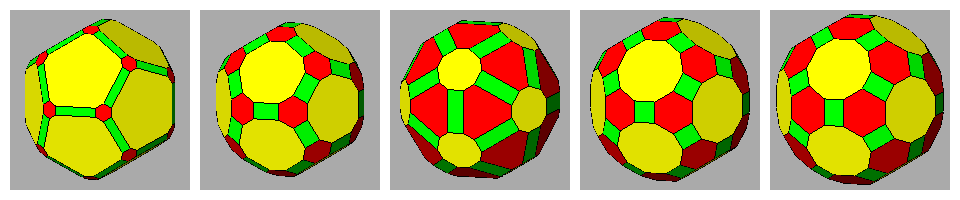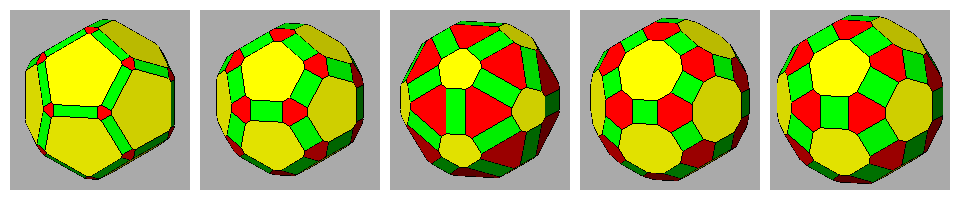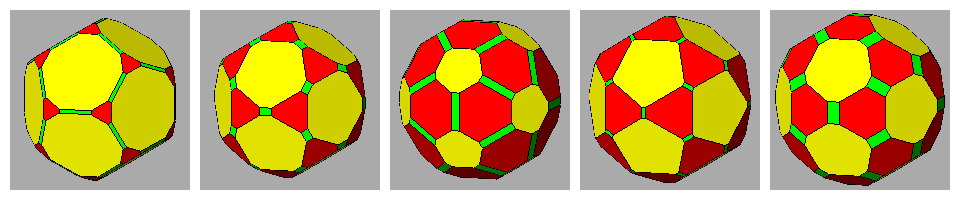 |
||||
|
FIG. 12 -
Sequences of vertex-transitive polyhedra deriving from the truncation by a rhomb-triacontahedron of:
A further decrease of the central distance of the intersecting rhomb-triacontahedron transforms the truncated icosidodecahedron in a vertex transitive polyhedron whose dual, analogously to the other four cases, is a face-transitive deltoid-hexecontahedron. |
||||
| CATALAN HEXAKIS-OCTAHEDRON | CATALAN HEXAKIS-ICOSAHEDRON |
 |
 |
|
FIG.13 - Face-transitive hexakis-octahedron (left) and hexakis-icosahedron (right), Catalan archetypes of the duals of the series of polyhedra deriving from the truncation processes. | |
| CATALAN DELTOID-ICOSITETRAHEDRON | CATALAN DELTOID-HEXECONTAHEDRON |
 |
 |
|
FIG.14 - Catalan deltoid-icositetrahedron (left) and deltoid-hexecontahedron (right), archetypes of the duals of the vertex-transitive polyhedra being the final result of each truncation process. | |
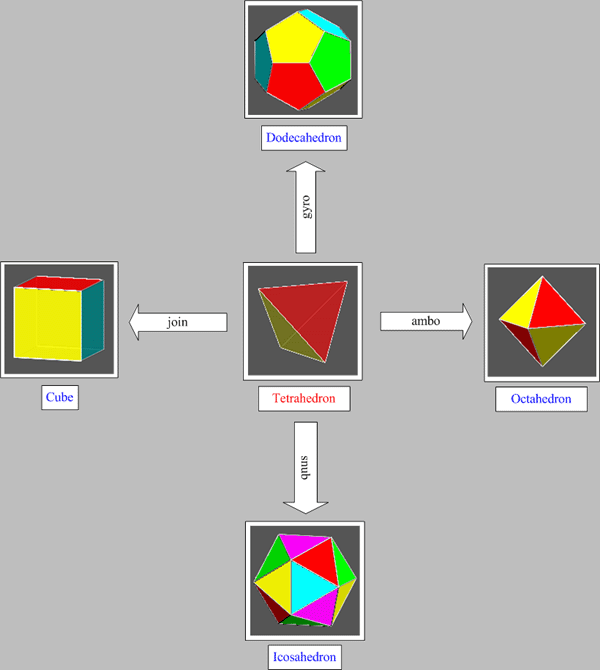
FROM THE TETRAHEDRON TO THE ARCHIMEDEAN TRUNCATED TETRAHEDRON
The tetrahedron is the fifth Platonic solid; it plays a singular role among the regular convex polyhedra, because of some peculiar features:
|
|
FIG.16 - Conway operators linking tetrahedron to the other
four Platonic solids. |
 |
 |
|
FIG. 17 - Sequences of the reciprocal truncation of {111} and {111} tetrahedra, leading to the same final form, geometrically identical to an octahedron. |
|
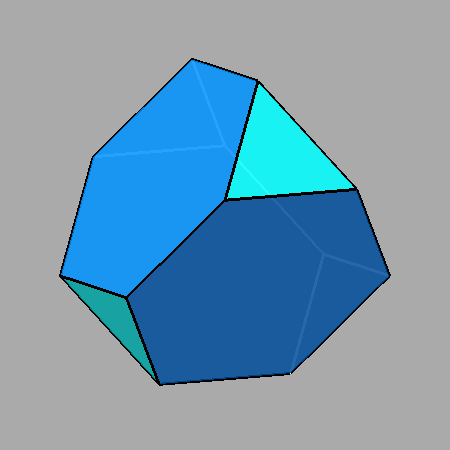 |
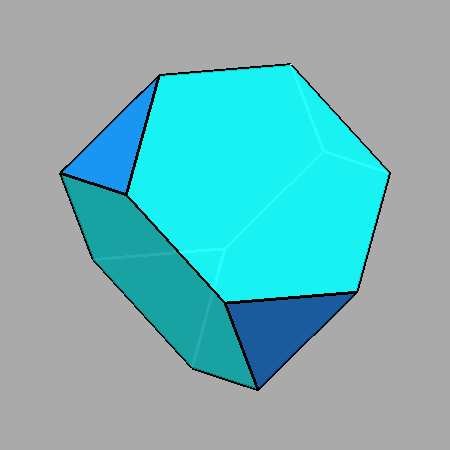 |
|
FIG.18 - Couple of views of the Archimedean truncated tetrahedron, obtained when the value of the ratio d{111} /d{111} between the distances of the tetrahedra {111} and {111} from the center of the solid is 5/3 (left) or 3/5 (right). |
|
 |
 |
|
FIG.19 - Couple of congruent Catalan triakis-tetrahedra {311} and {311}, duals of the Archimedean truncated tetrahedron, set in two alternative orientations, 90 degrees apart. In each Catalan polyhedron all the dihedral angles between couples of contiguous faces have a constant value: in case of the triakis-tetrahedron such value is 50.48°. |
|
 |
 |
|
FIG.20 - (left) Composite form, resulting from the intersection of the Archimedean truncated tetrahedron with the Catalan triakis-tetrahedra {311}, and (right) the relative dual form, made of a cube and the deltoid-dodecahedron {221}. | |
 |
|
FIG. 21 - Animated sequence describing the progressive edge-truncation process deriving from the intersection between the Archimedean truncated tetrahedron and a cube having decreasing dimensions. |
The choice of selected frames from the sequence allows to highlight the more interesting steps of the edge-truncation process (left column of Fig. 22) and the relative duals are shown in the right column. The lower row of each frame reports also the corresponding stereographic projection between the views, along the vertical [001] direction, of the couple of dual polyhedra.
|
Intermediate polyhedra (and relative duals) resulting from the progressive truncation of the Archimedean truncated tetrahedron by a cube |
|
 |
 |
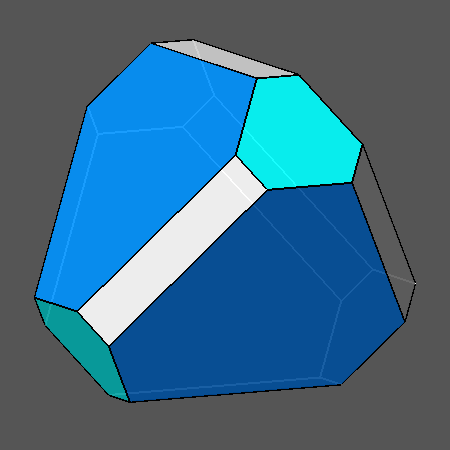
a) d{111}= √3/3;
d{111}= 5√3/9
Archimedean truncated tetrahedron
(the faces of the cube are tangent to six edges of the truncated tetrahedron when d{100}= 1.0) |
a') catalan triakis-tetrahedron {311} |
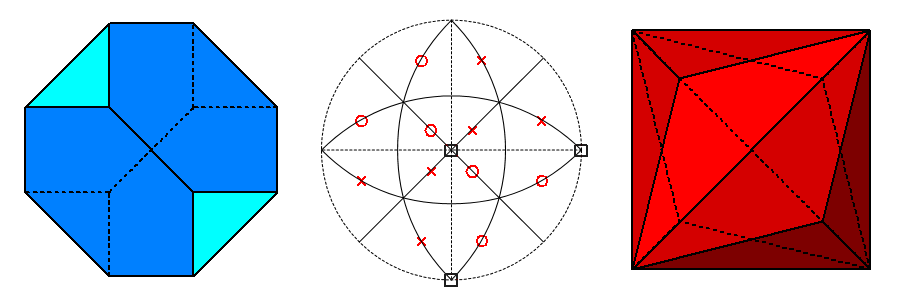
| |
 |
 |
|
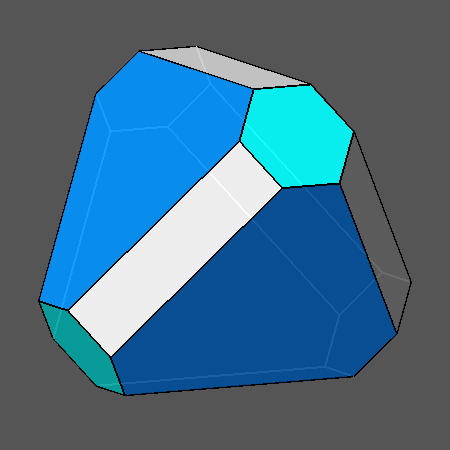
b) d{111}= √3/3; d{111}= 5√3/9; d{100}= 5/6 |
b') hexakis-tetrahedron {523} |
| |
 |
 |
| c) d{111}= √3/3; d{111}= 5√3/9; d{100}= 7/9 | c') hexakis-tetrahedron {735} |
| |
 |
 |
| d) d{111}= √3/3; d{111}= 5√3/9; d{100}= 3/4 | d') hexakis-tetrahedron {947} |
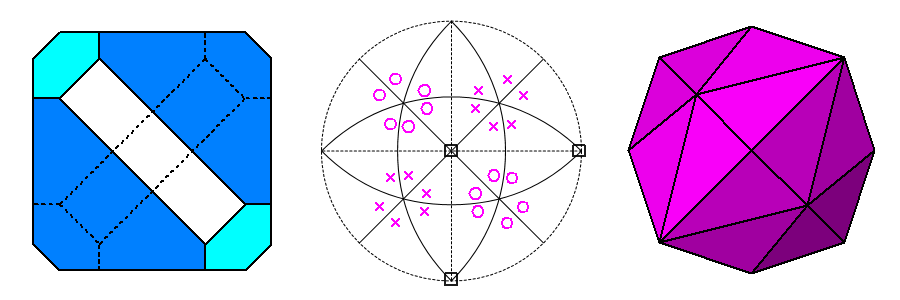
| |
 |
 |
| e) d{111}= √3/3; d{111}= 5√3/9; d{100}= 2/3 | e') deltoid-dodecahedron {212} |
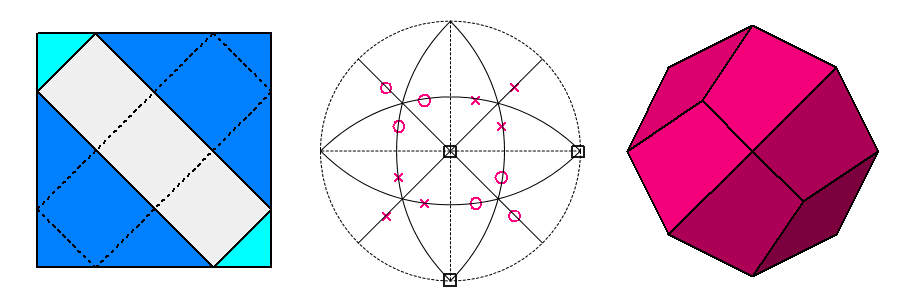
| |
 |
 |
| f) d{111}= √3/3; d{111}= 5√3/9; d{100}= 3/5 | f') {979} and {313} deltoid-dodecahedra |
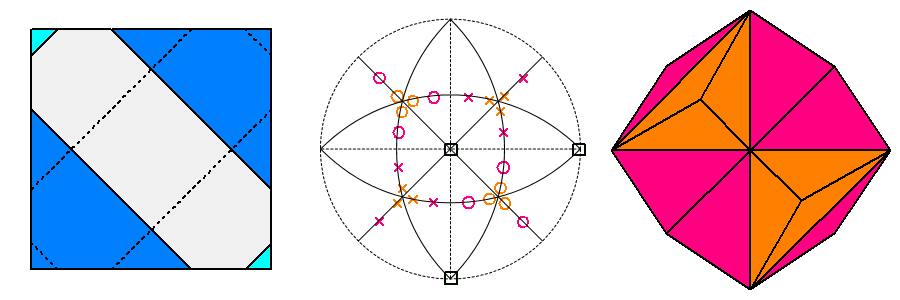
| |
 |
 |
| g) d{111}= √3/3;
d{111}= 5√3/9;
d{100}=
5/9 (the decreased central distance of the cube causes the disappearance of the more distant {111} tetrahedron) |
g') tetrahedron {111} and |
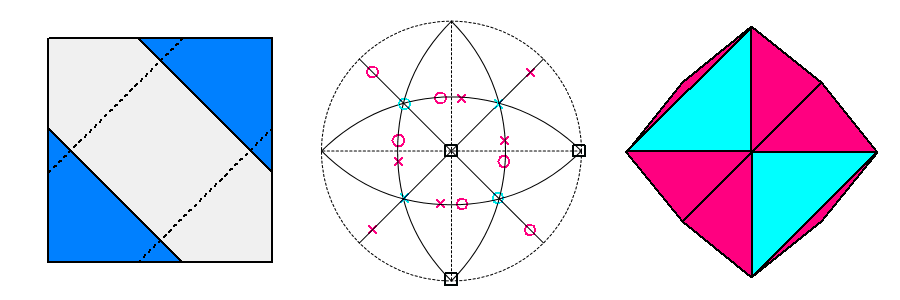
| |
 |
 |
|
h) d{111}= √3/3; d{111}= 5√3/9; d{100}= 1/2 |
h') tetrahedron {111} and rhomb-dodecahedron {101} |
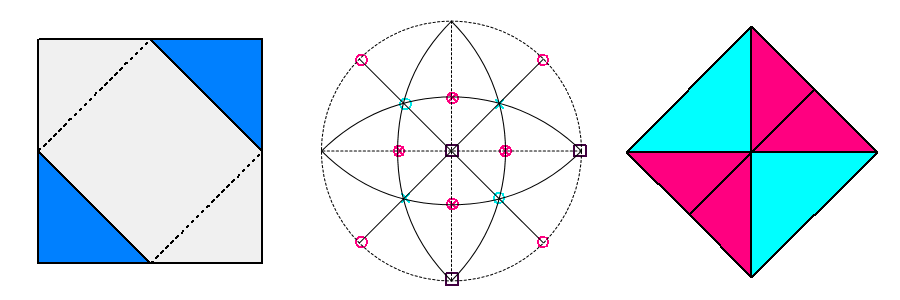
| |
 |
 |
| i) d{111}= √3/3; d{111}= 5√3/9; d{100}= 2/5 |
i') tetrahedron {111} and |
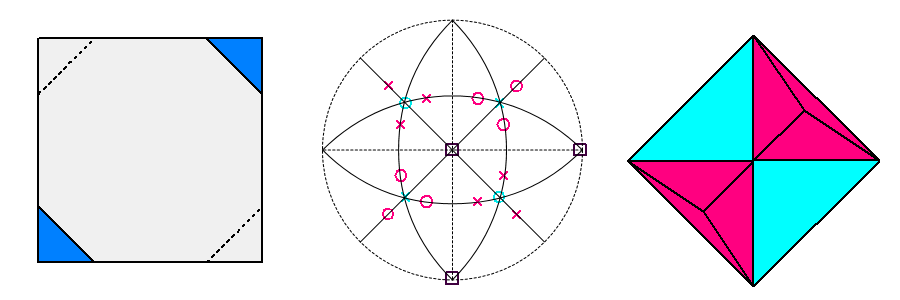
| |
 |
 |
|
j) d{111}= √3/3;
d{111}= 5√3/9;
d{100}= 1/3
(due to the intersecting cube, also the remaining tetrahedron has disappeared) |
j') {111} and {111} tetrahedra |
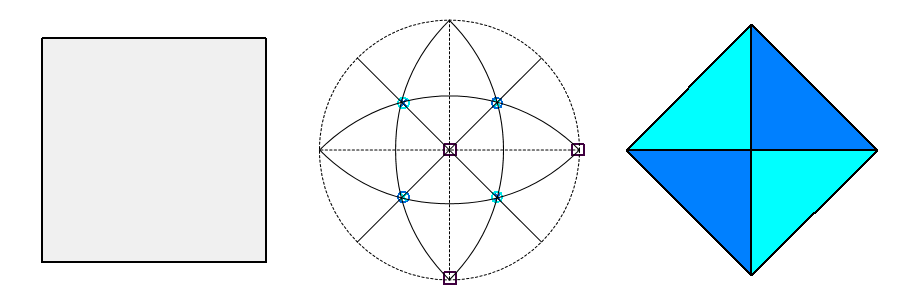
| |
|
FIG: 22 - Selected frames of the animated sequence reported in Fig.20, illustrating the more significant steps of the progressive truncation by a cube of the Archimedean truncated tetrahedron. The polyhedron obtained at each step is shown on the left of the upper row, whereas the relative dual is shown on the right; the stereographic projection of the faces of the dual polyhedron are reported in the lower row, between the views along the vertical [001] direction of the couple of dual polyhedra. | |
| First row d{100} = 1 |
When d{100}= 1.0 the
faces of the cube are just tangent to six edges of the Archimedean
truncated tetrahedron and do not intersecate it: therefore the solid in (a) consists in the Archimedean truncated tetrahedron,
made of triangular and hexagonal faces, both regular, and the solid in
(a') consists in its dual,
the {311} Catalan triakis-tetrahedron, having twelve faces.
|
| Second row d{100} = 5/6 |
As a consequence of the beginning of the truncation by
the cube,
the faces coming from both tetrahedra assume the shape of a non-regular
hexagon,
whereas the faces of the cube are rectangular; since each vertex
(shared by three faces, one of the cube and two of the different tetrahedra) is equivalent by symmetry to
all the other 23 vertices,
the form in (b) is vertex-transitive (or isogonal) and its dual shown in
(b') is the face-transitive (or isohedral)
hexakis-tetrahedron {523}, having twenty-four faces. |
| Third row d{100} = 7/9 |
In (c) the smaller hexagonal faces become regular in consequence of the increased truncation; consequently, in the dual {735} hexakis-tetrahedron shown in (c'), the dihedral angles between each couple of contiguous faces included in the set of six faces sharing a vertex along the direction [111] are all equal (17.860°). |
| Fourth row d{100} = 3/4 |
In (d) the faces derived from both tetrahedra have again the shape of non-regular hexagons; the dual isohedral form, shown in (d'), is the {947} hexakis-tetrahedron. |
| Fifth row d{100} = 2/3 |
In (e) the
truncation originates a form, having only twelve
vertices, which is still vertex-transitive: the faces derived from both tetrahedra have the shape of
equilateral triangles (having different sizes) and each vertex is shared by four faces: a couple of
rectangular faces coming from the cube, the two others from the couple of
tetrahedra. |
| Sixth row d{100} = 3/5 |
Since two are the different vertices present in (f),
the result of the truncation is a form that is not vertex-transitive: each vertex is shared by three faces,
two coming from the cube and the third, alternatively, from each of the two tetrahedra. |
| Seventh row d{100} = 5/9 |
This is another noteworthy stage of the
truncation process, since (g) marks the
complete disappearance of one of the tetrahedra. The number of vertices
decreases to sixteen: twelve are still shared by two faces of cube and a
face of the remaining tetrahedron, whereas the other four are shared by three faces belonging to
the only cube. |
| Eighth row d{100} = 1/2 |
The number of vertices is sixteen
even in (h), but the twelve vertices shared
by two faces of cube and a face of tetrahedron are now localized along [110] and
equivalent directions. |
| Ninth row d{100} = 2/5 |
The decreased central distance of the
faces of the cube causes in ( i ) the
progressive reduction of the size of the faces belonging to the remaining
tetrahedron. |
| Tenth row d{100} = 1/3 |
In (j) even the second tetrahedron disappears, lefting the only cube; in consequence of the 43m point group symmetry, its dual shown in (j') is a pseudo-octahedron, actually resulting from the intersection of the tetrahedron {111} and the tetrahedron {111}. |
 |
|
FIG. 23 - Animated sequence including the duals of the forms obtained by the intersection between the Archimedean truncated tetrahedron and a cube with decreasing size (to be compared with Figure 21). |
LINKS AND REFERENCES