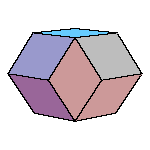
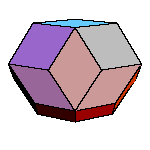
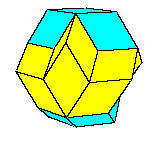
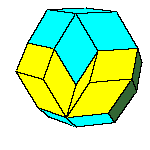
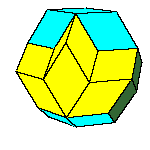
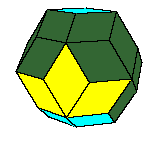
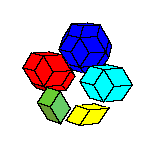Introduction to golden rhombic polyhedra
Izidor Hafner
Tomislav Zitko
Faculty of Electrical Engineering, University of Ljubljana
Trzaska 25
, 1000 Ljubljana
, Slovenia
e-mail: izidor.hafner@fe.uni-lj.si
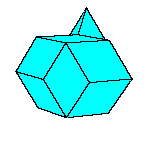
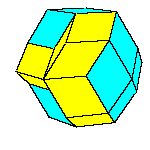
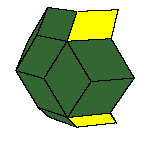
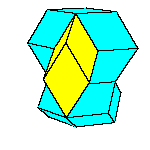
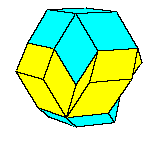
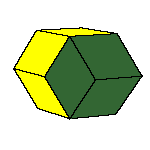
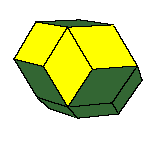
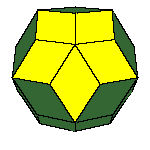
There is a family of isohedral rhombic polyhedra that consists of prolate and obtuse rhombohedron, (rhombic)
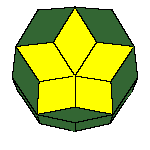
dodecahedron of the second kind, discovered by Bilinski in 1960, rhombic icosahedron, discovered by Fedorov in 1885
and triacontahedron, discovered by Kepler in 1611 [
P. R. Cromwell, Polyhedra, Cambridge U. Pr., 1997].
Only the last one has icosahedral symmetry. The faces of these solids are congruent rhombs whose
diagonals are in golden ratio. The last three solids could be constructed by gluing appropriate number of
rhombohedra [
T. Ogawa, Symmetry of three-dimensional quasicrystals].
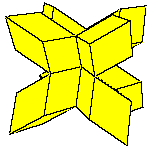
These five solids are the only convex polyhedra of this kind. Some nonconvex polyhedra
are constructed.
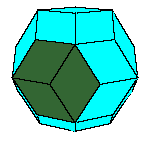
The convex rhombic solids are also zonohedrons[
G.Hart,
V.Bulatov
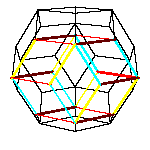
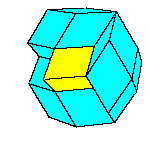
]. By contraction of one zone of a triacontahedron we obtain an
icosahedron, from the later we get a dodecahedron, then a rhombohedron and a dihedron at the end.
When using
LiveGraphics3D:
dragging (rotating about an axis in the picture), releasing left mouse button while
dragging (spinning about an axis in the picture), Shift key pressed plus horizontal dragging (rotating about an axis
perpendicular to the picture), Control key pressed plus horizontal dragging (changing focal length).
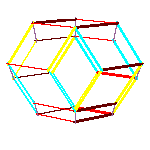
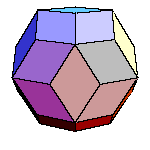
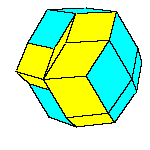
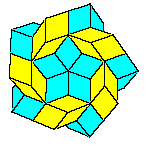
All convex rhombic solids can be constructed by gluing some number of rhombohedra. For a dodecahedron we need 2
rhombohedra of each kind, for an icosahedron we need 5 and for a triacontahedron 10 rhombohedra of each kind.
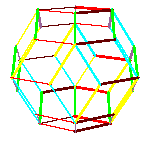
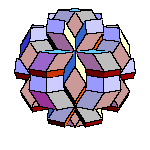
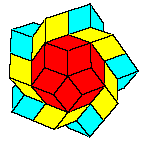
By gluing 20 oblate rhombohedra we get a hexecontahedron. If we put 30 dodecaheda on a triacontahedron, we get a
210-hedron. Both have the icosahedral symmetry. More on polyhedra with icosahedral symmetry see
I.Hafner...
Animations
Exercises
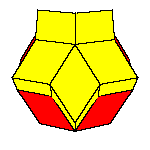
Take 2 rhombohedra of each kind and make a rhombic dodecahedron.
Take a dodecahedron and 3 rhombohedra of each kind and make a rhombic icosahedron.
Take a icosahedron and 5 rhombohedra of each sort and make a triacontahedron. If the triacontahedron is made from
rhombohedra only, how many of them are needed?
Take three dodecahedra and some rhombohedra and make a triacontahedron.
Take two dodecahedra, form a letter T from them and add some rhombohedra to get a triacontahedron.
VisMathHOME