

: A new type of
: Combinatorial Games and Beautiful
: A chocolate problem that
The list of P-positions of the chocolate problem of Example 3.1 produces very beautiful graphs.
The authors are going to present these graphs, and after that they are present graphs produced by other variants of chocolate problem.
Example 4.1.
We are going to find P-positions of Game 2.
The list 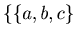 , a
, a 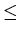 60, b
60, b 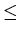 60, c
60, c 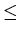 60 and
60 and 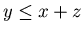
 has 226981 positions of Game 2, and we are going to find P-positions in this list.
has 226981 positions of Game 2, and we are going to find P-positions in this list.
By calculating Grundy numbers we can get P-positions in the list. The list of P-positions has 3547 elements. Since this is a big list, we are going to present a part of it here.
{{0, 0, 0}, {1, 0, 1}, {1, 1, 2}, {1, 2, 3}, {1, 3, 4}, {1, 4, 5}, {1,
5, 6}, {1, 6, 7}, {1, 7, 8}, {1, 8, 9}, {1, 9, 10}, {1, 10, 11}, {1, 11, 12}, {1, 12, 13}, {1, 13, 14}, {1, 14, 15}, {1, 15, 16}, ...}
Example 4.2.
We are going to change the order of the list. First we sort the list according to the size of the second coordinate, i.e., the size of b in {a,b,c}.
Then we have {{a,b,c}; b = 0}, {{a,b,c}; b = 1}, {{a,b,c}; b = 2}, .
.. After that we sort elements in {{a,b,c}; b = k }
according to the size of a. Then we have the following list.
{{0,0,0},{1,0,1},{2,0,2},{3,0,3},{4,0,4},{5,0,5},..
{1,1,2},{2,1,1},{3,1,4},{4,1,3},{5,1,6},{6,1,5},...
{1,2,3},{2,2,4},{3,2,1},{4,2,2},{5,2,7},{6,2,8},...
Example 4.3.
After that we replace {a,b,c}
by {a,b,c-a},
then we can get a very interesting strucuture of data. We denote this data by Data.
Data = {{0,0,0},{1,0,0},{2,0,0},{3,0,0},{4,0,0},{5,0,0},...
{{1,1,1},{2,1,-1},{3,1,1},{4,1,-1},{5,1,1},{6,1,-1},...
{{1,2,2},{2,2,2},{3,2,-2},{4,2,-2},{5,2,2},{6,2,2},...
{{1,3,3},{2,3,1},{3,3,-1},{4,3,-3},{5,3,3},{6,3,1},...
{7,3,-1},{8,3,-3},{9,3,3},{10,3,1},{11,3,-1},{12,3,-3},...
{{1,4,4},{2,4,4},{3,4,4},{4,4,4},{5,4,-4},{6,4,-4},...}
If you make a 3D graph of Data, then you get the following graph.
By rotation we get another 3D graph. It seems that there is a Sierpinski gasket in this graph.
The authors have projected 3D graph onto many planes, and finally they have discovered Graph 4.3.
By rotation we get another 3D graph.
Example 4.4.
By the same method we used in Example 4.1 we can make 3D graphics for another chocolate problem.
This chocolate problem has inequality
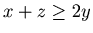 instead of
instead of
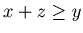 .
.
It is interesting to compare Graph 4.7 and Graph 4.3.
Example 4.5.
By the same method we used in Example 4.1 we can make 3D graphics for another chocolate problem.
This chocolate problem has inequality
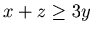 instead of
instead of
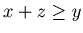 .
.
It is interesting to compare Graph 4.10 and Graph 4.3.
Example 4.6.
By the same method we used in Example 4.1 we can make 3D graphics for another chocolate problem.
This chocolate problem has inequality
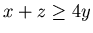 instead of
instead of
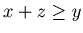 .
.
Example 4.7.
By the same method we used in Example 4.1 we can make 3D graphics for another chocolate problem.
This chocolate problem has inequality
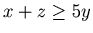 instead of
instead of
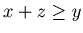 .
.
It is interesting to compare Graph 4.16, Graph 4.7 and Graph 4.3. It seems
that an inequality with an odd cofficient of y produces the Sierpinski
gasket, and an inequality with an even cofficient of y produces a more
complicated figures.
Example 4.8.
By the same method we used in Example 4.1 we can make 3D graphics for another chocolate problem.
This chocolate problem has inequality
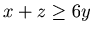 instead of
instead of
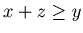 .
.
Remark 4.1.
The graphs in Example 4.3, 4.4, 4.5, 4.6, 4.7 and 4.8 are beautiful and interesting, but the authors have studied the mathematical structure only for the chocolate problem of Example 4.1.
As to the mathematical structure of other chocolate problems the authors have not discovered anything.


: A new type of
: Combinatorial Games and Beautiful
: A chocolate problem that
![\includegraphics[height=7cm,width=10cm,clip]{chocoxyz1.eps}](img126.gif)
![\includegraphics[height=7cm,width=10cm,clip]{chocoxyz2.eps}](img127.gif)
![\includegraphics[height=7cm,width=10cm,clip]{chocoxyz3.eps}](img128.gif)
![\includegraphics[height=7cm,width=10cm,clip]{chocoxyz4.eps}](img129.gif)
![\includegraphics[height=7cm,width=10cm,clip]{chocox2yz1.eps}](img131.gif)
![\includegraphics[height=7cm,width=10cm,clip]{chocox2yz2.eps}](img132.gif)
![\includegraphics[height=7cm,width=10cm,clip]{chocox2yz3.eps}](img133.gif)
![\includegraphics[height=7cm,width=10cm,clip]{chocox3yz1.eps}](img135.gif)
![\includegraphics[height=7cm,width=10cm,clip]{chocox3yz2.eps}](img136.gif)
![\includegraphics[height=7cm,width=10cm,clip]{chocox3yz3.eps}](img137.gif)
![\includegraphics[height=7cm,width=10cm,clip]{chocox4yz1.eps}](img139.gif)
![\includegraphics[height=7cm,width=10cm,clip]{chocox4yz2.eps}](img140.gif)
![\includegraphics[height=7cm,width=10cm,clip]{chocox4yz3.eps}](img141.gif)
![\includegraphics[height=7cm,width=10cm,clip]{chocox5yz1.eps}](img143.gif)
![\includegraphics[height=7cm,width=10cm,clip]{chocox5yz2.eps}](img144.gif)
![\includegraphics[height=7cm,width=10cm,clip]{chocox5yz3.eps}](img145.gif)
![\includegraphics[height=7cm,width=10cm,clip]{chocox6yz1.eps}](img147.gif)
![\includegraphics[height=7cm,width=10cm,clip]{chocox6yz2.eps}](img148.gif)
![\includegraphics[height=7cm,width=10cm,clip]{chocox6yz3.eps}](img149.gif)