|
Other infinite series
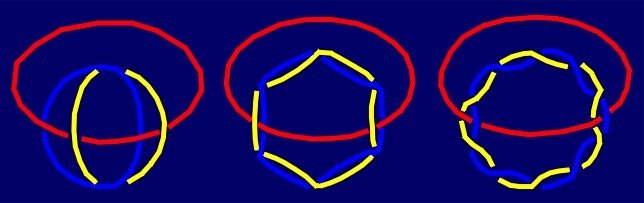
The next infinite series of 3-Borromean links, beginning again with the Borromean rings,
follow from a circular 2-component trivial links by introducing the third component:
a circle intersecting the projection in opposite points.
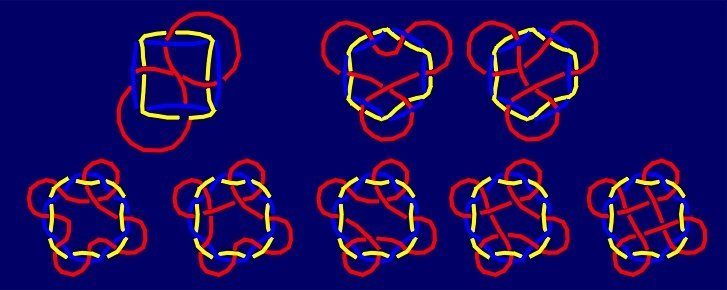
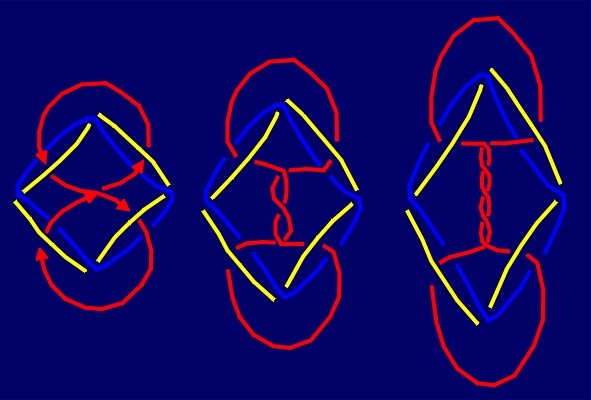
In a similar way,
from the family of 2-component trivial links we derive the other infinite
series of 3-component Borromean links.
|